3.1.4 Fonctions de distribution cumulative
Fonction de distribution cumulative
Les distributions de probabilité peuvent être définies de différentes manières selon la description de la variable aléatoire utilisée, mais elles peuvent toujours être définies par une fonction de distribution cumulative (FDC; aussi appelée « fonction de répartition »). Cette fonction décrit la probabilité que la variable aléatoire ne dépasse pas une valeur donnée – autrement dit, 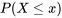 .
.
Chaque distribution de probabilité reposant sur des valeurs réelles est définie par une fonction continue à droite et non décroissante ![{\displaystyle F\colon \mathbb {R} \rightarrow [0,1]} {\displaystyle F\colon \mathbb {R} \rightarrow [0,1]}](https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/77202eb9c5f3bc68098624bfd57bc61a.png) telle que
telle que 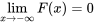 et
et 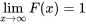 . Toute fonction possédant ces quatre propriétés est une FDC : pour chaque fonction de ce type, on peut définir une variable aléatoire qui a cette fonction pour fonction de distribution cumulative.
. Toute fonction possédant ces quatre propriétés est une FDC : pour chaque fonction de ce type, on peut définir une variable aléatoire qui a cette fonction pour fonction de distribution cumulative.
Définition 3.1.4.1. Fonction de distribution cumulative (FDC)
La fonction de probabilité cumulative d’une variable aléatoire X est une fonction F(x) qui, pour chaque nombre x, donne la probabilité que X prenne cette valeur ou une valeur plus petite. Symboliquement :
![F(x)=P[X \leq x] F(x)=P[X \leq x]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/02661d769255dee69404659ee6e5a9c0.png)
