3.1.3 Variables aléatoires et distributions de probabilités
Caractère aléatoire et variation
Nous avons vu que la nature aléatoire représente l’élément fondamental du hasard, comme dans le cas du jeu de pile ou face, mais elle peut également représenter l’incertitude, comme dans le cas d’une erreur de mesure. Après avoir introduit le concept d’événements et d’expériences aléatoires dans le chapitre précédent, considérons maintenant qu’une expérience consiste à prendre une mesure numérique issue d’une expérience d’ingénierie. Les données de mesures comportent généralement une part de hasard et sont soumises à des influences fortuites. Dans l’échantillonnage statistique et les études de fréquence, le hasard est introduit par les techniques d’échantillonnage. Le hasard est également introduit par l’erreur de mesure. Il peut y avoir d’autres sources de hasard, dont les nombreuses petites causes non identifiées qui influent sur la mesure du phénomène aléatoire. Dans les contextes analytiques, les changements dans les conditions du système font varier les réponses mesurées, ce qui est le plus souvent attribué au hasard.
Quel que soit le soin apporté à la conception et à la réalisation d’une expérience, des variations se produisent souvent en raison de ces phénomènes fortuits. L’objectif est donc de comprendre, de quantifier et de modéliser la variation, puis de l’exploiter dans nos analyses afin de tirer des conclusions basées sur les données qui restent valides malgré cette variation.
Variables aléatoires et distribution des probabilités
Une variable aléatoire est une formalisation mathématique, ou fonction, d’un événement qui dépend d’une expérience aléatoire sous-jacente. Il s’agit d’une variable associée à une variable réelle qui attribue une valeur numérique à chaque résultat possible de l’expérience.
Dans la plupart des cas, une variable aléatoire  est une fonction faisant correspondre un espace échantillon (un espace de mesure de la probabilité) à des nombres réels (un espace mesurable) :
est une fonction faisant correspondre un espace échantillon (un espace de mesure de la probabilité) à des nombres réels (un espace mesurable) :
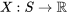
Ainsi, il est possible de créer la distribution mathématique d’une variable aléatoire conforme aux axiomes de probabilité. Cette distribution fournit la mesure de probabilité ![{\displaystyle [0,1]\subseteq \mathbb {R} } {\displaystyle [0,1]\subseteq \mathbb {R} }](https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/511efe69c491a34ed7846e6fe78029c8.png) associée à chacune des valeurs possibles de la variable aléatoire. Les variable aléatoires sont exprimées sous la forme de lettres latines majuscules, souvent celles de la fin de l’alphabet, comme
associée à chacune des valeurs possibles de la variable aléatoire. Les variable aléatoires sont exprimées sous la forme de lettres latines majuscules, souvent celles de la fin de l’alphabet, comme 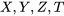 .
.
Pour l’exemple simple de pile ou face, on utilise une fonction qui fait correspondre aux valeurs de l’espace échantillon de 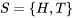 une valeur mesurable de l’espace
une valeur mesurable de l’espace 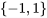 , où 1 correspond à P et -1 correspond à F, en utilisant la variable aléatoire
, où 1 correspond à P et -1 correspond à F, en utilisant la variable aléatoire  pour représenter la mesure aléatoire de l’expérience.
pour représenter la mesure aléatoire de l’expérience.
Une fois défini l’espace échantillon de 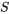 par la variable aléatoire correspondante
par la variable aléatoire correspondante  , il est désormais possible de se poser la question : « Quelle est la probabilité que la valeur de
, il est désormais possible de se poser la question : « Quelle est la probabilité que la valeur de  soit égale à +1? ». C’est la probabilité de l’événement =
soit égale à +1? ». C’est la probabilité de l’événement = 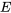 =
= 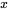 = +1, qu’on note
= +1, qu’on note 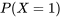 .
.
Consigner toutes les probabilités des sorties d’une variable aléatoire  permet d’obtenir la distribution de probabilité de
permet d’obtenir la distribution de probabilité de  . Une distribution de probabilité est la fonction mathématique qui définit les probabilités que l’événement (le sous-ensemble défini de l’espace échantillon) se produise. Elle définit donc l’expérience aléatoire en termes de l’événement.
. Une distribution de probabilité est la fonction mathématique qui définit les probabilités que l’événement (le sous-ensemble défini de l’espace échantillon) se produise. Elle définit donc l’expérience aléatoire en termes de l’événement.
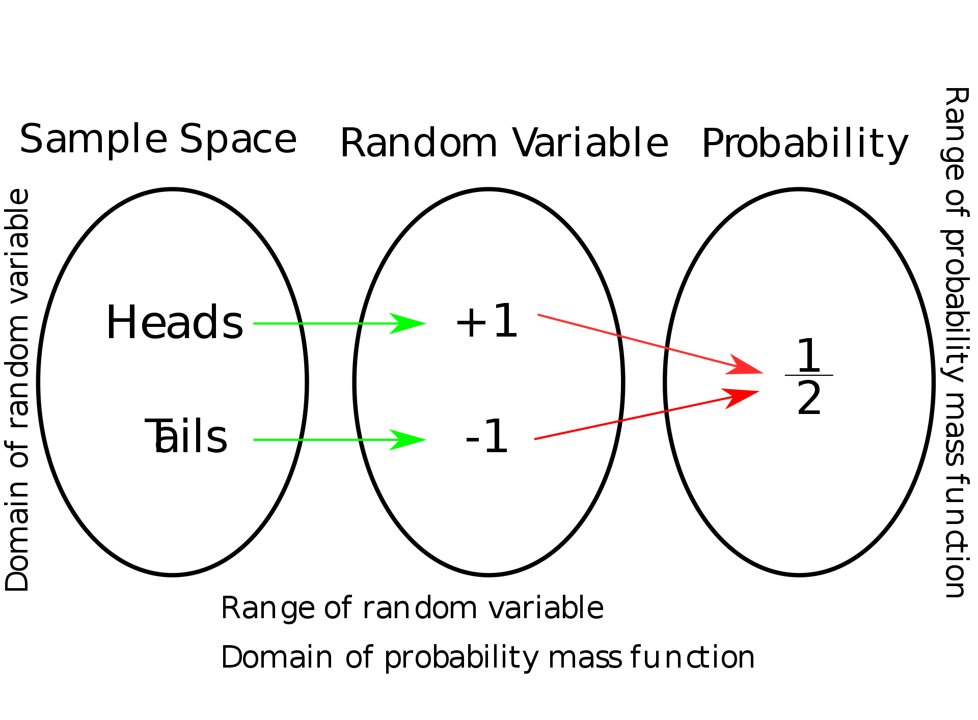
Pour l’exemple du pile ou face, si  est la variable aléatoire utilisée pour définir le résultat aléatoire de l’expérience, la distribution de probabilité de
est la variable aléatoire utilisée pour définir le résultat aléatoire de l’expérience, la distribution de probabilité de  prend alors la valeur 0,5 (ou 1/2) pour
prend alors la valeur 0,5 (ou 1/2) pour  = Pile, et 0,5 pour
= Pile, et 0,5 pour  = Face.
= Face.
Principaux points à retenir
Révision des termes relatifs aux variables aléatoires et aux distributions de probabilités :
- Variable aléatoire : à partir de valeurs d’un espace échantillon, attribue des probabilités en fonction de la probabilité de l’événement expérimental.
- Événement : ensemble des valeurs possibles (résultats) d’une variable aléatoire qui se produit avec une certaine probabilité,
- Distribution de probabilité : fonction qui fournit la probabilité d’occurrence des événements pour l’expérience, ou
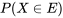 pour un événement.
pour un événement.
