3.1.1 Probabilité d’événements aléatoires

Probabilité

Les probabilités sont le cadre mathématique concernant les événements d’une activité particulière et les descriptions numériques des chances qu’ils se produisent..  Il s’agit d’une mesure, à laquelle on attribue un nombre compris en 0 et 1 (inclusivement), qui est associée à la certitude des résultats.

Commençons par réviser un peu de terminologie liée aux probabilités :

Terminologie des probabilités :

  • Une expérience est un processus (une activité particulière, une expérience, un phénomène ou une opération planifiée réalisée dans des conditions contrôlées ) qui produit une observation.
  • Un résultat est le résultat mutuellement exclusif des observations possibles d’une expérience.
  • Par « résultats mutuellement exclusifs », on entend qu’un seul des résultats possibles peut être observé.
  • L’ensemble de tous les résultats possibles forme ce que l’on appelle un espace échantillon (aussi appelé univers).
  • Un événement est un sous-ensemble de l’espace échantillon.
  • Un essai est une exécution unique d’une expérience.

Événements aléatoires

Le hasard et l’incertitude existent dans toutes les expériences, dans la vie quotidienne et partout dans le monde, ainsi que dans toutes les disciplines de la médecine, de la science et de l’ingénierie.  Une expérience aléatoire est une expérience dans laquelle le résultat existe mais n’est ni prédéterminé, ni connu.  Un événement aléatoire est donc le sous-ensemble de l’espace échantillon d’une expérience aléatoire.  Jouer à pile ou face est un exemple d’expérience aléatoire, puisque le résultat de pile ou face est incertain.  L’espace échantillon peut être représenté par une liste de l’ensemble, un diagramme de Venn, un schéma en arbre ou un tableau de contingence.  Ces méthodes peuvent être utiles lorsqu’on commence à attribuer et à calculer des probabilités pour des événements multiples.

Nous utiliserons des lettres majuscules pour désigner un ensemble et énumérerons tous les résultats entre crochets.  Par exemple, pour définir un espace échantillon de l’expérience aléatoire de type pile ou face: 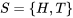S = \{P, F\} où P = pile et F = face sont les résultats.  L’espace échantillon correspondant à lancer une fois deux pièces de monnaie s’exprime comme suit : S = {(PP),(PF),(FP),(FF)}.  Nous utiliserons également des lettres majuscules pour désigner un événement, comme A et B. Par exemple, on peut définir l’événement A comme le fait d’obtenir pile sur la première pièce, et l’événement B, comme le fait d’obtenir pile sur la deuxième pièce.  Cela se traduirait par 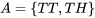A = \{PP, PF\} et B = \{PP, FP\}.  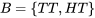Les diagrammes sont utiles pour représenter ensemble les opérations de plusieurs événements.

Diagramme de Venn

Un diagramme de Venn est la représentation visuelle d’un espace échantillon et d’événements sous forme de cercles ou d’ovales montrant leurs intersections.  Dans l’exemple ci-dessus, où l’on tire deux fois à pile ou face, on a l’événement A et l’événement B, et le résultat 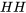FF n’est ni dans 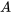A ni dans 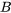B. Le diagramme de Venn est alors représenté comme suit :

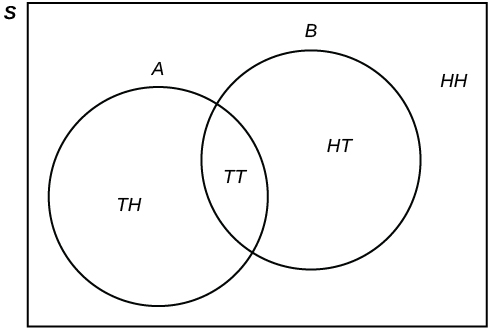
Il s’agit d’un diagramme de Venn. Un ovale représentant l’ensemble A contient Pile + Face et Pile + Pile. Un ovale représentant l’ensemble B contient également Pile + Pile, ainsi que Face + Pile. L’univers S contient aussi Face + Face, mais cette valeur n’est ni dans l’ensemble A ni dans l’ensemble B.

Pile ou face avec deux pièces normales : [latex]A = \{PP, PF\}[/latex] et [latex]B = \{PP, FP\}[/latex]. Par conséquent, [latex]A \text{ ET } B[/latex]  = [latex]A \text{  INTERSECTION } B[/latex] = [latex]A \cap B[/latex] = [latex]\{PP\}[/latex]. [latex]A \text{ OU } B = A \text{ UNION } B[/latex] = [latex]A \cup B[/latex]  = [latex]\{PF, PP, FP\}[/latex].
Schéma en arbre
Un schéma en arbre est une représentation d’un espace échantillon et d’événements sous la forme d’un « arbre » dont les branches sont marquées par les résultats possibles.
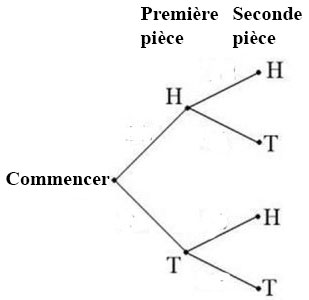
Tableau de contingence

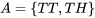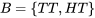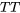Les tableaux de contingence classent les résultats et les événements.  Ces tableaux contiennent des lignes et des colonnes qui affichent des fréquences à deux variables de données catégoriques.  Les événements conjoints se produisent ensemble dans une cellule, comme, pour l’exemple ci-dessus, les événements conjoints de A = \{PP, PF\} et de B = \{PP, FP\} = {PP}.  Les événements marginaux sont ceux qui figurent en marge du tableau et qui se produisent pour un seul événement, sans tenir compte des autres événements du tableau.  Dans cet exemple, le tableau contient un événement marginal A auquel sont associés les événements conjoints A = \{PP, PF\}.

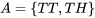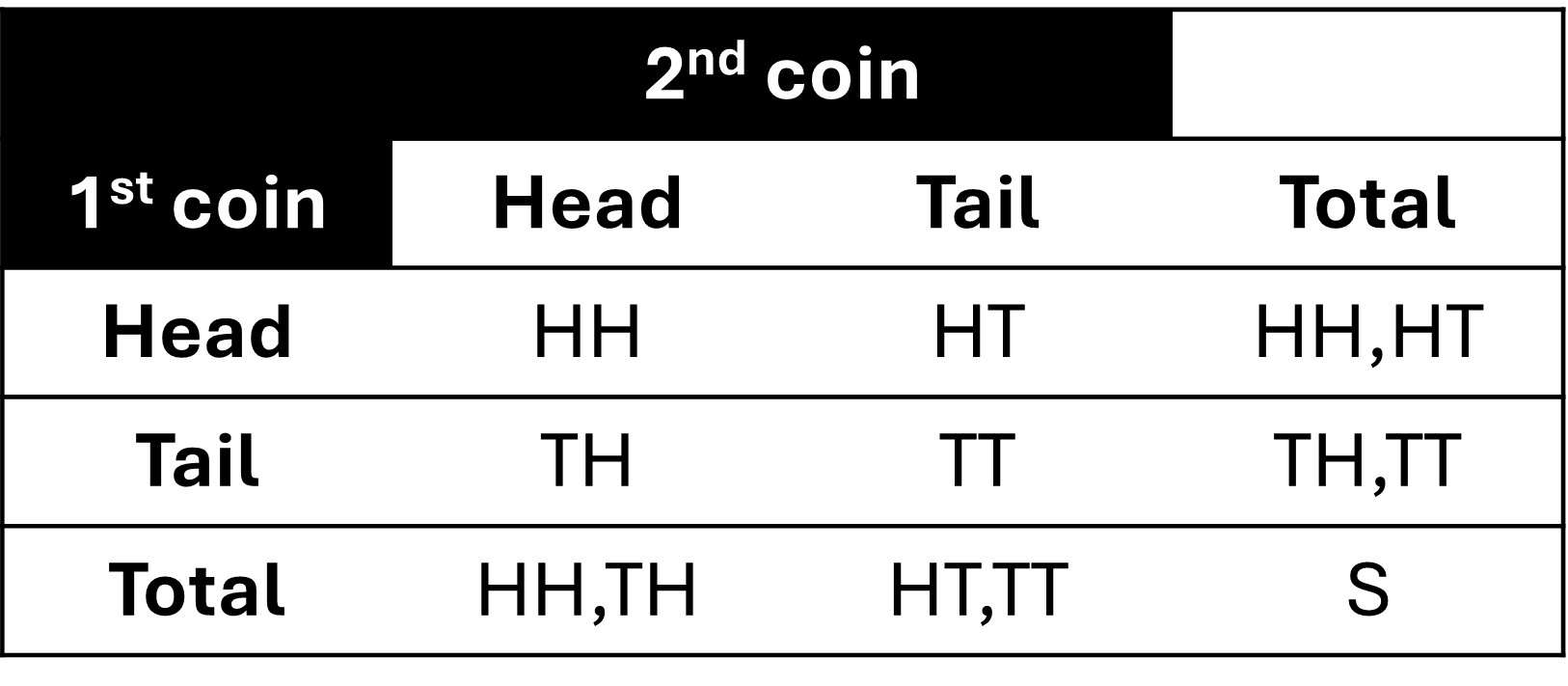
Théorie des ensembles

Les événements des expériences aléatoires étant des ensembles, nous passerons en revue quelques notions de base de la théorie des ensembles :

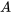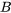Soient A et B des événements d’un espace échantillon.

  • Si un élément 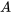A appartient à un ensemble 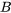B, on l’indique par le symbole \in.
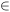  • L’ensemble vide est représenté par le symbole 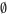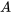\emptyset.
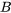  • A et B sont disjoints (ou mutuellement exclusifs) si A \cap B = \emptyset.
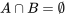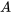  • A est un sous-ensemble de 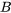B si chaque élément de 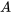A se trouve également dans 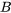B. On écrit alors A ⊂ B.

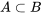Pour les événements multiples, on peut donc énoncer :

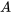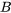Soient A et B des événements d’un espace échantillon.

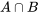  • A \cap B est l’ensemble des résultats qui se trouvent à la fois dans 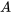A et B.
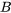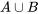  • A \cup B est l’ensemble des résultats qui ne sont dans 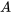A ou dans  B 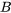ou dans les deux.
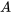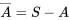  • Le complément de A est \overline{A} = S - A.  Par conséquent, 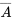\overline{A} est l’ensemble de résultats qui ne sont pas dans A.

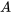Théorie des probabilités

L’utilité des probabilités est d’attribuer des chances d’occurrence raisonnables à des événements possibles dans le cadre d’expériences aléatoires.  Avant d’examiner quelques applications pratiques, voyons comment on peut interpréter la théorie des probabilités dans le cadre d’expériences aléatoires.

Les probabilités représentent une quantification du degré de conviction personnelle subjective qu’un événement se produira dans le cadre d’une expérience aléatoire.  L’approche subjective la plus courante consiste à utiliser les probabilités bayésiennes, mais cela dépasse le cadre de ce cours.  Pour simplifier, on peut considérer que la probabilité est la proportion d’occurrences d’un événement favorable par rapport au nombre total de résultats possibles dans un espace échantillon à probabilité uniforme.  Une autre interprétation repose sur la quantification des résultats objectifs d’expériences aléatoires.  Cette approche fréquentiste des probabilités est à la base de la plupart des cours d’introduction aux statistiques et d’une grande partie des méthodes statistiques. C’est ce cadre que nous utiliserons pour exploiter le caractère aléatoire des expériences aléatoires.

Les probabilités fréquentistes énoncent que la probabilité d’un événement aléatoire est la fréquence relative de l’événement lorsque l’expérience est répétée indéfiniment.  Cette interprétation est souvent énoncée comme étant la fréquence relative d’une expérience « à la longue » ou « à long terme ».  Étant donné un événement A dans un espace échantillon, la fréquence relative de A est le rapport 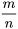\frac{m}{n}, où m est le nombre de résultats d’occurrences de l’événement A, et n le nombre total de résultats de l’expérience.  L’approche fréquentiste affirme qu’au fur et à mesure que le nombre d’essais augmente, la variation de la fréquence relative diminue. La probabilité est donc la valeur limite des fréquences relatives correspondantes. On peut déterminer la fréquence relative soit en réalisant des expériences réelles et en trouvant une probabilité empirique (ou estimée), soit en reconnaissant le modèle théorique de l’expérience et en adoptant une probabilité théorique basée sur les événements de l’espace échantillon.

Dans le cas d’un espace échantillon où les résultats sont équiprobables :

Si les résultats d’un espace échantillon fini S ont tous la même probabilité, alors pour tout événement A :

P[A] = 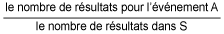\frac{\text{le nombre de résultats dans l’événement A}}{\text{le nombre de résultats dans S}}

Le terme équiprobable signifie que les résultats d’une expérience ont tous la même probabilité de se produire. Par exemple, si on tire à pile ou face avec une pièce de monnaie, il est tout aussi probable d’obtenir pile (P) que face (F). On peut donc compter le nombre de résultats pour l’événement A = obtenir une fois face, et le diviser par le nombre total de résultats dans l’espace échantillon. Si on lance deux pièces, l’espace échantillon est {PP, PF, FP, FF}.  Deux résultats répondent à cette condition, soient {PF, FP}, donc P(A) = 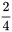\frac = 0,5.

Ce texte utilisera la convention de notation selon laquelle un P majuscule suivi d’une expression ou d’une phrase entre crochets signifie « la probabilité » de cette expression. P(A) est donc la probabilité du résultat A.

À long terme, la fréquence relative du tirage à pile ou face s’approchera de la probabilité théorique de 0,5.  Comme il n’y a que deux résultats possibles, cette probabilité empirique de succès, en tant que fréquence relative expérimentale, convergera vers la probabilité théorique. La loi des grands nombres dit qu’à mesure que le nombre d’essais augmente, les valeurs de l’échantillon tendent à converger vers le résultat attendu.  Autrement dit, la proportion de faces dans un « grand » nombre de tirages à pile ou face « devrait être » d’environ 0,5. Plus précisément, la proportion de faces après n lancés convergera vers 0,5 quand n tend vers l’infini. Même si les résultats ne suivent pas de modèle prédéterminé, dans l’ensemble, la fréquence relative observée à long terme s’approchera de la probabilité théorique.

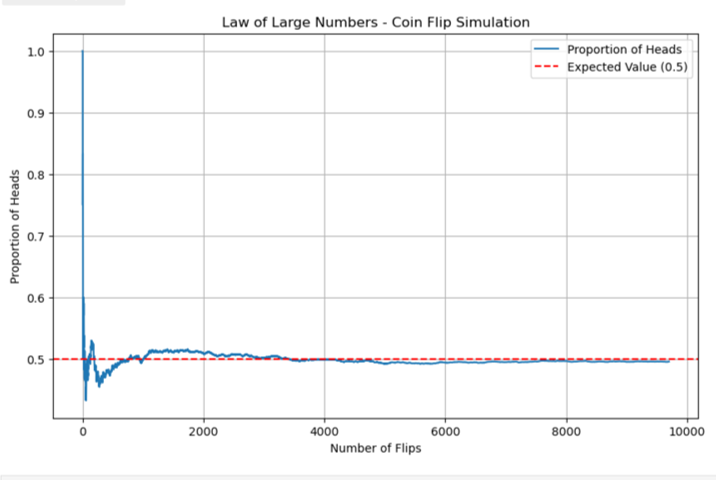
Voir le Jupyter Notebook dans le référentiel GitHub pour une simulation de cette démonstration de jeu de pile ou face à long terme : CoinTossSimulation.

 

Licence

Introduction aux méthodes statistiques en ingénierie© par C. Bassim et Bryan Lee. Tous droits réservés.

Partagez ce livre