2.2.5 Diagramme à barres et graphiques de données qualitatives ou de dénombrement
Les techniques présentées jusqu’à présent dans ce chapitre concernent principalement l’analyse des données de mesure. Comme nous l’avons mentionné dans la partie 1, les données de mesure (ou données de variables) sont généralement préférables, si on peut les obtenir, aux données chiffrées et aux données qualitatives (ou données d’attributs). Néanmoins, les données qualitatives ou de dénombrement sont parfois les principales informations disponibles. Il est donc intéressant d’étudier leur synthèse et leur visualisation.
Souvent, une étude produit plusieurs valeurs de 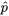 ou
ou 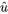 qui doivent être comparées. Les diagrammes en barres et les diagrammes simples à deux variables peuvent être d’une grande aide pour résumer ces résultats.
qui doivent être comparées. Les diagrammes en barres et les diagrammes simples à deux variables peuvent être d’une grande aide pour résumer ces résultats.
Example 2.2.5.1. Classification des connecteurs de câble selon leur défaut.
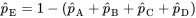 , car les catégories A à E constituent un ensemble de catégories exhaustives et mutuellement exclusives, de sorte que la somme des
, car les catégories A à E constituent un ensemble de catégories exhaustives et mutuellement exclusives, de sorte que la somme des 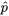 doit valoir 1.
doit valoir 1.
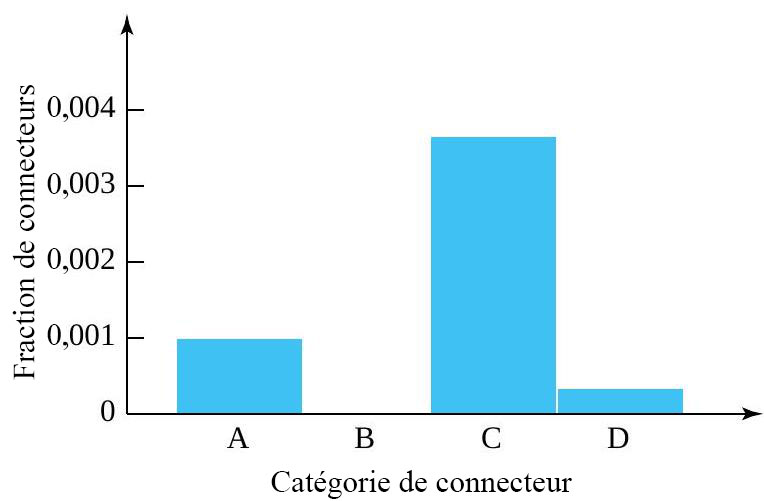
La figure 2.2.5.1 est un diagramme à barres des fractions de connecteurs des catégories A à D. Elle montre clairement que la plupart des connecteurs présentant des défauts appartiennent à la catégorie  , celle des défauts modérément graves, mais ni graves ni très graves. Ce diagramme à barres présente le comportement d’une variable catégorique.
, celle des défauts modérément graves, mais ni graves ni très graves. Ce diagramme à barres présente le comportement d’une variable catégorique.
Example 2.2.5.2. Fabrication d’outils pneumatiques.
Kraber, Rucker et Williams ont travaillé avec un fabricant d’outils pneumatiques. Chaque outil produit est minutieusement inspecté avant d’être expédié. Les étudiant.e.s ont recueilli des données sur plusieurs types de problèmes découverts lors de l’inspection finale. Le tableau 2.2.5.2 indique le nombre d’outils présentant ces problèmes dans une série de 100 outils.
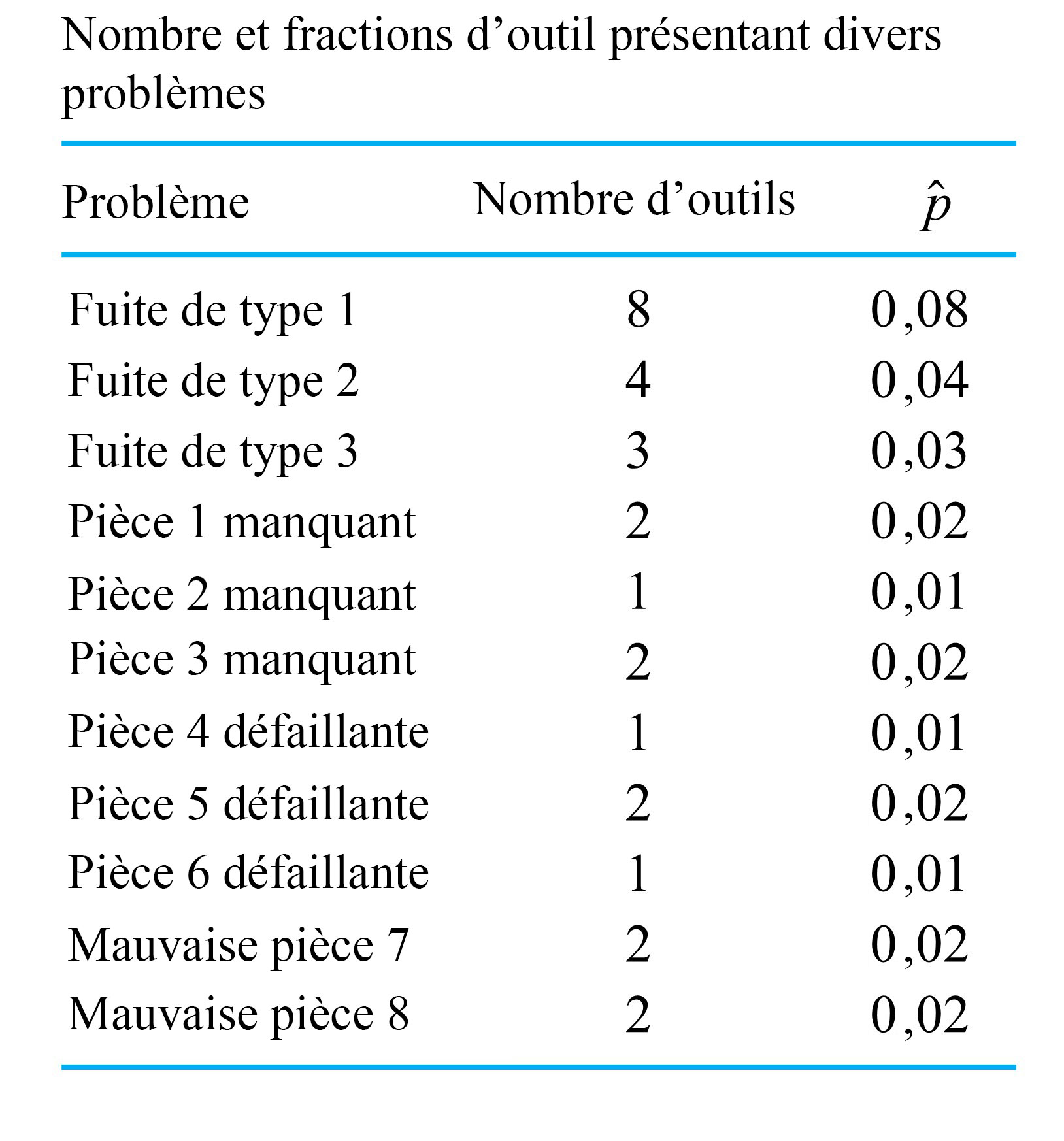
Ce tableau est une synthèse de données qualitatives à plusieurs variables. Les catégories énumérées dans le tableau 2.2.5.2 ne sont pas mutuellement exclusives; un outil donné peut être compté dans plusieurs catégories. Au lieu de représenter différentes valeurs possibles d’une seule variable catégorique (comme c’était le cas avec les catégories de connecteurs dans l’exemple 2.2.5.1), ces catégories sont construites selon deux conditions possibles (présence ou absence), et leur valeur correspond au dénombrement des présences. Par exemple, pour les types de fuites 1, 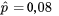 , donc la proportion d’outils ne présentant pas le type de fuite 1 est
, donc la proportion d’outils ne présentant pas le type de fuite 1 est 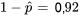 . Le total des valeurs
. Le total des valeurs 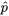 n’est pas forcément égal à la fraction des outils problématiques lors de l’inspection finale. Un outil défectueux donné peut être comptabilisé dans plusieurs valeurs
n’est pas forcément égal à la fraction des outils problématiques lors de l’inspection finale. Un outil défectueux donné peut être comptabilisé dans plusieurs valeurs 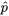 .
.
La figure 2.2.5.2 représente un diagramme à barres des informations sur les problèmes d’outils figurant dans le tableau 2.2.5.1. Elle montre que les fuites sont les problèmes les plus fréquents sur cette série de production.
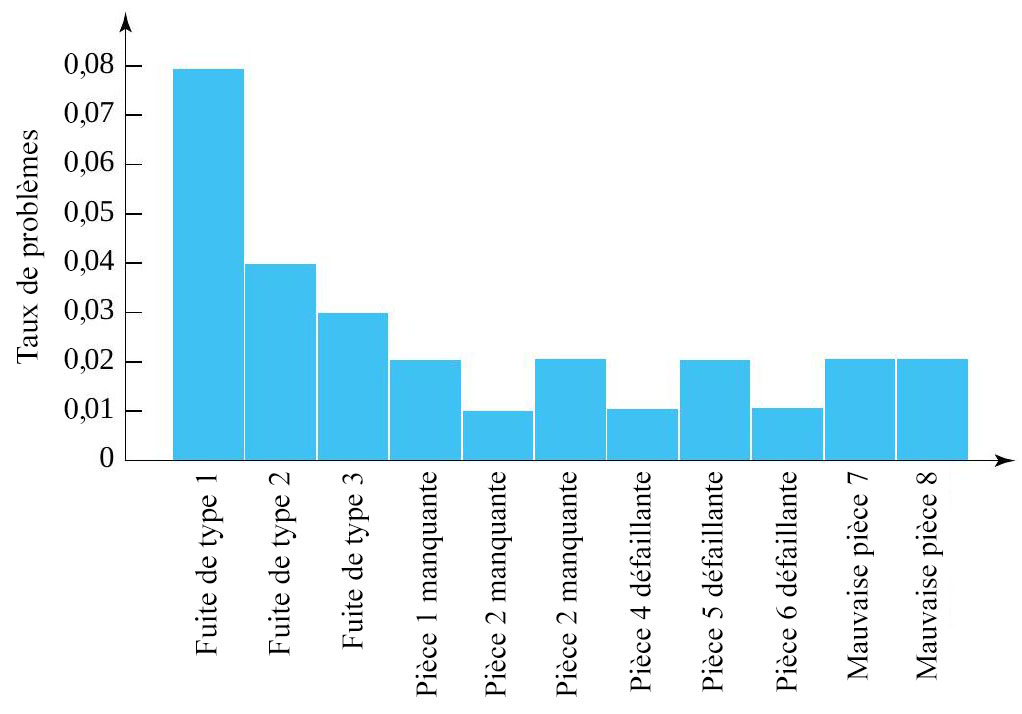
Les figures 2.2.5.1 et 2.2.5.2 illustrent toutes deux des diagrammes à barres, mais elles diffèrent considérablement. La première montre le comportement d’une seule variable catégorique (ordonnée), à savoir la classe de connecteur. La seconde concerne le comportement de 11 variables catégoriques présence-absence différentes, comme la fuite de type 1, la pièce 3 manquante, etc. La forme de la figure 2.2.5.1 peut avoir une certaine signification, car les catégories A à D sont classées par ordre décroissant de gravité des défauts, et c’est cet ordre qui a été utilisé dans la figure. Mais la forme de la figure 2.2.5.2 est essentiellement arbitraire, puisque l’ordre des catégories de problèmes d’outils est lui-même arbitraire. D’autres ordres tout aussi sensés donneraient des formes tout à fait différentes.
