2.2.1 Mesures de position
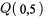 , qui a été présentée dans la dernière section. La médiane divise un ensemble de données en deux. Dans un histogramme bien conçu, environ la moitié de l’aire des barres se situe de part et d’autre de la médiane. En tant que mesure du centre, elle est totalement insensible aux effets de quelques observations extrêmes ou aberrantes. Par exemple, le petit ensemble de données
, qui a été présentée dans la dernière section. La médiane divise un ensemble de données en deux. Dans un histogramme bien conçu, environ la moitié de l’aire des barres se situe de part et d’autre de la médiane. En tant que mesure du centre, elle est totalement insensible aux effets de quelques observations extrêmes ou aberrantes. Par exemple, le petit ensemble de données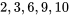
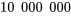 et si la valeur 2 est remplacée par
et si la valeur 2 est remplacée par 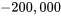 .
.DÉFINITION 2.2.1.1. Moyenne arithmétique.
La moyenne (arithmétique) d’un échantillon de données quantitatives, par exemple 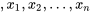 , correspond à
, correspond à
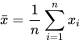
 .
.Exemple 2.2.1.1. Perte des rouleaux de papier
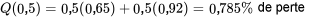

Pour le fournisseur 2,
[latex]Q(0,5) = 0,5(1,47) + 0,5(1,58) = 1,525 \% \text { de pertes }[/latex]
et

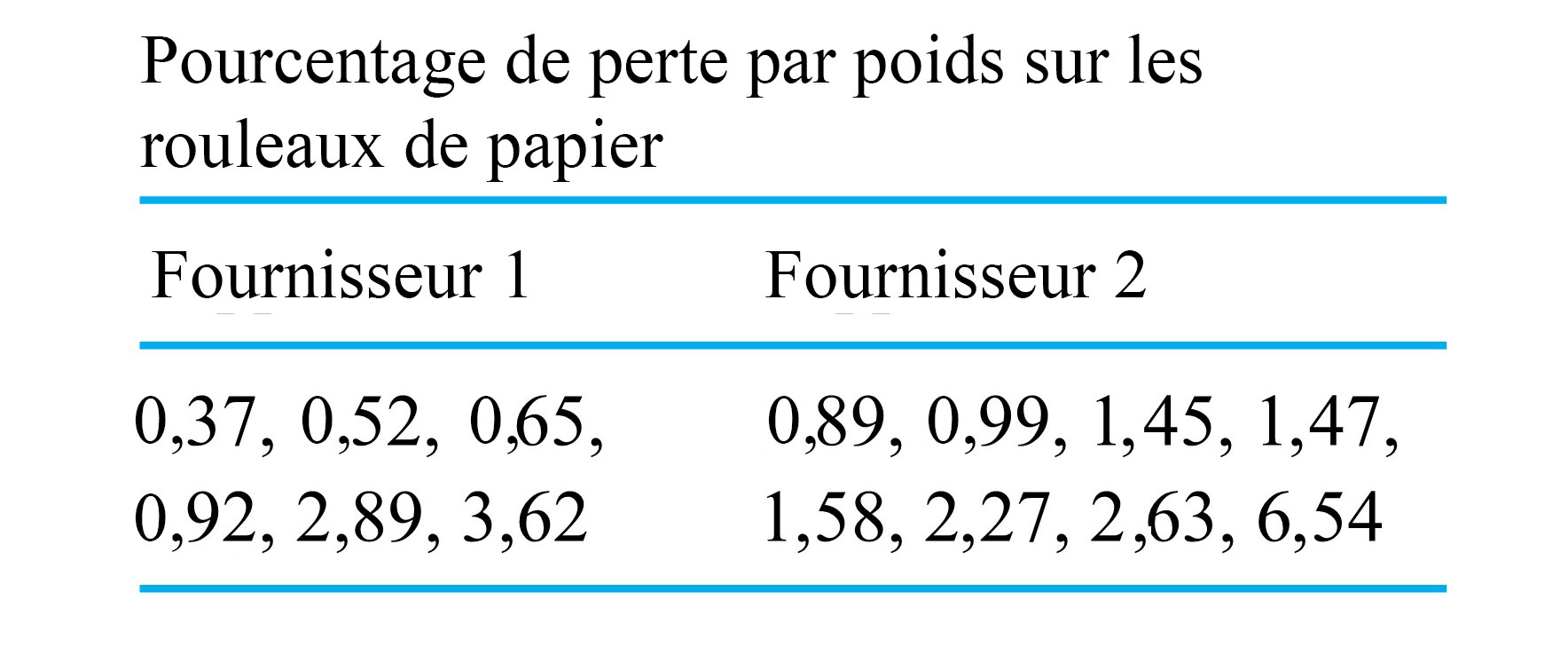
La figure 2.2.1.1 illustre des diagrammes à points sur lesquels on a indiqué la médiane et la moyenne. Remarquez que les médianes et les moyennes des deux fournisseurs montrent que les pertes du fournisseur 2 sont plus importantes que celles du fournisseur 1. Notez également qu’il existe une différence substantielle entre les valeurs médianes et moyennes pour un fournisseur donné. Dans les deux cas, la moyenne est nettement supérieure à la médiane correspondante. Cela reflète la nature asymétrique à droite des deux ensembles de données. Dans les deux cas, le centre de masse de la distribution est fortement tiré vers la droite par quelques valeurs extrêmement élevées.
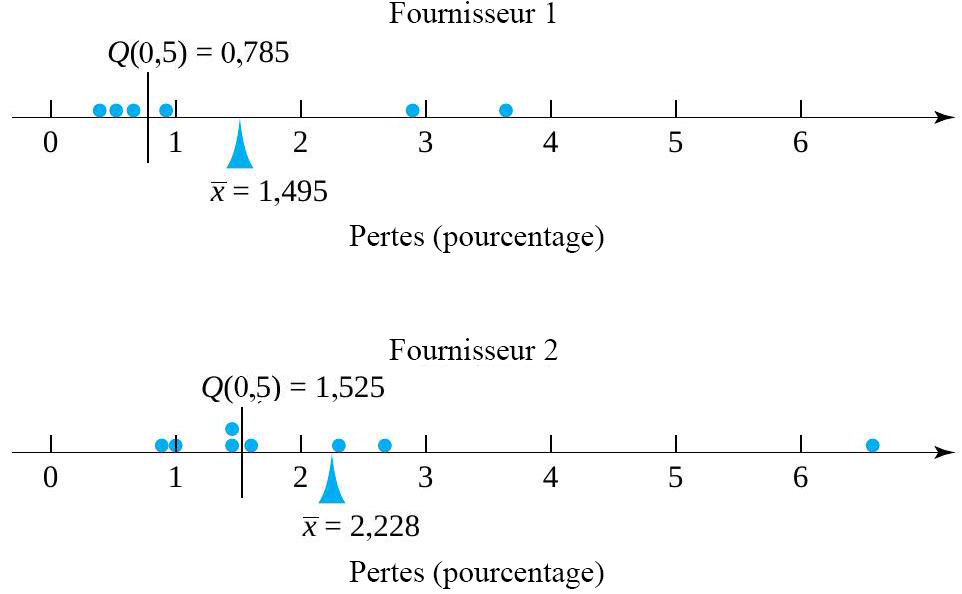
L’exemple 2.2.1.1 montre clairement que, contrairement à la médiane, la moyenne est une mesure centrale qui peut être fortement influencée par quelques valeurs extrêmes. Certaines personnes disent parfois que, pour cette raison, l’une ou l’autre des deux mesures est « meilleure » – une affirmation qui n’a aucun sens. Ni l’une ni l’autre n’est meilleure; il s’agit simplement de mesures ayant des propriétés différentes. Et ces différences, les personnes averties qui lisent des statistiques doivent les garder à l’esprit. Par exemple, le salaire « moyen » des employé.e.s d’une entreprise qui paie neuf personnes 10 000 $ par an et son président 110 000 $ par an peut être décrit comme 10 000 $ par an (médiane) ou 20 000 $ par an (moyenne).
