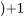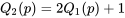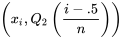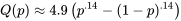2.1.7 Diagrammes Q-Q et comparaison des formes de distribution
 .
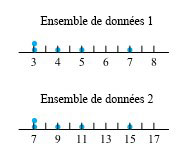
.2.1.7.1lae plus petite valeur de l’ensemble de données
e plus petite valeur de l’ensemble de données 1
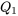 et
et 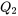 représenter les fonctions de quantiles des deux ensembles de données, on voit clairement à la figure 2.1.7.1 que
représenter les fonctions de quantiles des deux ensembles de données, on voit clairement à la figure 2.1.7.1 que2.1.7.2

petits ensembles de données.
.

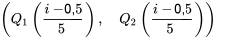
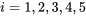 ) devrait être exactement linéaire. La figure 2.1.7.2 illustre cela – en fait la figure 2.1.7.2 est un diagramme
) devrait être exactement linéaire. La figure 2.1.7.2 illustre cela – en fait la figure 2.1.7.2 est un diagramme  pour les ensembles de données du tableau 2.1.7.1.
pour les ensembles de données du tableau 2.1.7.1.DÉFINITION 2.1.7.1. Diagramme 
Un diagramme  de deux ensembles de données avec des fonctions quantile respectives
de deux ensembles de données avec des fonctions quantile respectives 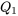 et
et 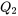 est un diagramme de paires ordonnées
est un diagramme de paires ordonnées 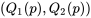 pour les valeurs appropriées de
pour les valeurs appropriées de  . Lorsque les deux ensembles de données sont de même taille
. Lorsque les deux ensembles de données sont de même taille  , les valeurs de
, les valeurs de  utilisées pour élaborer le diagramme seront
utilisées pour élaborer le diagramme seront 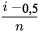 , avec
, avec 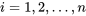 . Lorsque les ensembles de données sont de taille inégale, les valeurs de
. Lorsque les ensembles de données sont de taille inégale, les valeurs de  utilisées pour élaborer le diagramme seront
utilisées pour élaborer le diagramme seront 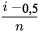 avec
avec 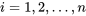 , où
, où  correspond à la taille de l’ensemble le plus petit.
correspond à la taille de l’ensemble le plus petit.
Étapes d’élaboration d’un diagramme Q-Q
 de deux ensembles de données de taille égale :
de deux ensembles de données de taille égale : raisonnablement linéaire indique que les deux distributions ont des formes similaires. Lorsqu’il y a des écarts significatifs par rapport à la linéarité, le caractère de ces écarts révèle la manière dont les formes diffèrent.
raisonnablement linéaire indique que les deux distributions ont des formes similaires. Lorsqu’il y a des écarts significatifs par rapport à la linéarité, le caractère de ces écarts révèle la manière dont les formes diffèrent.Exemple 2.1.7.1. Pénétration des balles (suite)
 . Il suffit d’associer les profondeurs de chaque ligne de ce tableau et de les tracer pour obtenir le tracé de la figure 2.1.7.3.
. Il suffit d’associer les profondeurs de chaque ligne de ce tableau et de les tracer pour obtenir le tracé de la figure 2.1.7.3.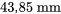 et
et 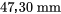 (pour les données des balles à 230 grains) est disproportionné par rapport à l’écart entre 63,55 et
(pour les données des balles à 230 grains) est disproportionné par rapport à l’écart entre 63,55 et 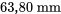 (pour les données des balles à 200 grains). Cela laisse supposer qu’il existe une différence physique fondamentale dans les mécanismes ayant causé la dispersion des données de profondeur des balles à 230 grains. Les statistiques peuvent révéler ce genre d’indice, mais pour expliquer les causes, il faut faire appel à des spécialistes de la balistique ou des matériaux.
(pour les données des balles à 200 grains). Cela laisse supposer qu’il existe une différence physique fondamentale dans les mécanismes ayant causé la dispersion des données de profondeur des balles à 230 grains. Les statistiques peuvent révéler ce genre d’indice, mais pour expliquer les causes, il faut faire appel à des spécialistes de la balistique ou des matériaux.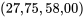 , il existe également une différence importante dans la forme des extrémités inférieures des deux distributions. Pour remettre ce point en ligne avec le reste des points tracés, il faudrait le déplacer vers la droite (augmenter la plus petite donnée des balles à 230 grains) ou vers le bas (diminuer la plus petite observation des balles à 200 grains). En d’autres termes, par rapport à la distribution des balles à 200 grains, la distribution des balles à 230 grains présente une longue queue inférieure. (Ou, autrement dit, par rapport à la distribution des balles à 230 grains, la distribution des balles à 200 grains a une queue inférieure courte.) À noter que la différence de forme était déjà évidente dans le diagramme en boîte de la figure précédente. Encore une fois, il faudrait un spécialiste pour expliquer cette différence dans les formes de distribution.
, il existe également une différence importante dans la forme des extrémités inférieures des deux distributions. Pour remettre ce point en ligne avec le reste des points tracés, il faudrait le déplacer vers la droite (augmenter la plus petite donnée des balles à 230 grains) ou vers le bas (diminuer la plus petite observation des balles à 200 grains). En d’autres termes, par rapport à la distribution des balles à 200 grains, la distribution des balles à 230 grains présente une longue queue inférieure. (Ou, autrement dit, par rapport à la distribution des balles à 230 grains, la distribution des balles à 200 grains a une queue inférieure courte.) À noter que la différence de forme était déjà évidente dans le diagramme en boîte de la figure précédente. Encore une fois, il faudrait un spécialiste pour expliquer cette différence dans les formes de distribution.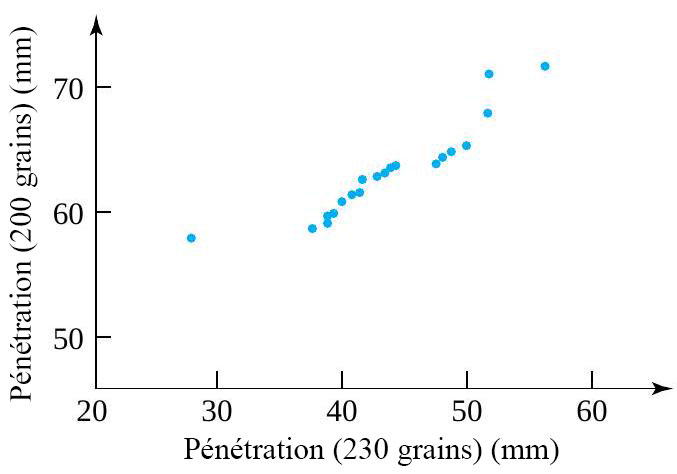
Le plus facile pour expliquer le concept de diagramme Q-Q (un outil très pratique pour comparer des jeux de donnés), c’est de voir une application où l’on compare des données empiriques. Mais le diagramme Q-Q est vraiment utile lorsqu’on l’applique à une fonction quantile qui représente un ensemble de données et à une seconde qui représente une distribution théorique.
DÉFINITION 2.1.7.2 Diagramme Q-Q théorique
Un diagramme Q-Q théorique, ou diagramme de probabilité, pour un ensemble de données de taille n et une distribution théorique, sont les fonctions quantiles sont respectivement Q1 et Q2, est un diagramme de paires ordonnées (Q1(p), Q2(p)) pour des valeurs appropriées de p. Dans cet ouvrage, les valeurs de p prennent la forme 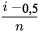 , avec i = 1, 2,…, n.
, avec i = 1, 2,…, n.
Soit Q (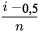 ) le ie point du petit ensemble de données, le
) le ie point du petit ensemble de données, le
diagramme Q-Q théorique est un diagramme de points dans lequel les abscisses correspondent aux données expérimentales, et les ordonnées, aux quantiles de la distribution théorique. Autrement dit, on utilise les données ordonnées x1 ≤ x2 ≤ ... ≤ xn pour tracer les points
2.1.7.3 Paires ordonnées d’un diagramme de probabilité
Un tel diagramme permet de poser la question suivante: « L’ensemble des données a-t-il une forme similaire à la distribution théorique? »
Tracé normal
 le plus connu est celui de la distribution normale (ou gaussienne), la distribution en forme de cloche bien. Le tableau 2.1.7.2 donne quelques quantiles de cette distribution. Pour trouver
le plus connu est celui de la distribution normale (ou gaussienne), la distribution en forme de cloche bien. Le tableau 2.1.7.2 donne quelques quantiles de cette distribution. Pour trouver 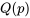 pour
pour  =
=  , on repère la ligne correspondant au premier chiffre après la décimale et la colonne correspondant au deuxième chiffre après la décimale. (Par exemple,
, on repère la ligne correspondant au premier chiffre après la décimale et la colonne correspondant au deuxième chiffre après la décimale. (Par exemple, 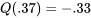 .) Pour approximer les valeurs du tableau 2.1.7.2, on peut utiliser la relation suivante :
.) Pour approximer les valeurs du tableau 2.1.7.2, on peut utiliser la relation suivante :2.1.7.3 Approximation des quantiles normaux standards
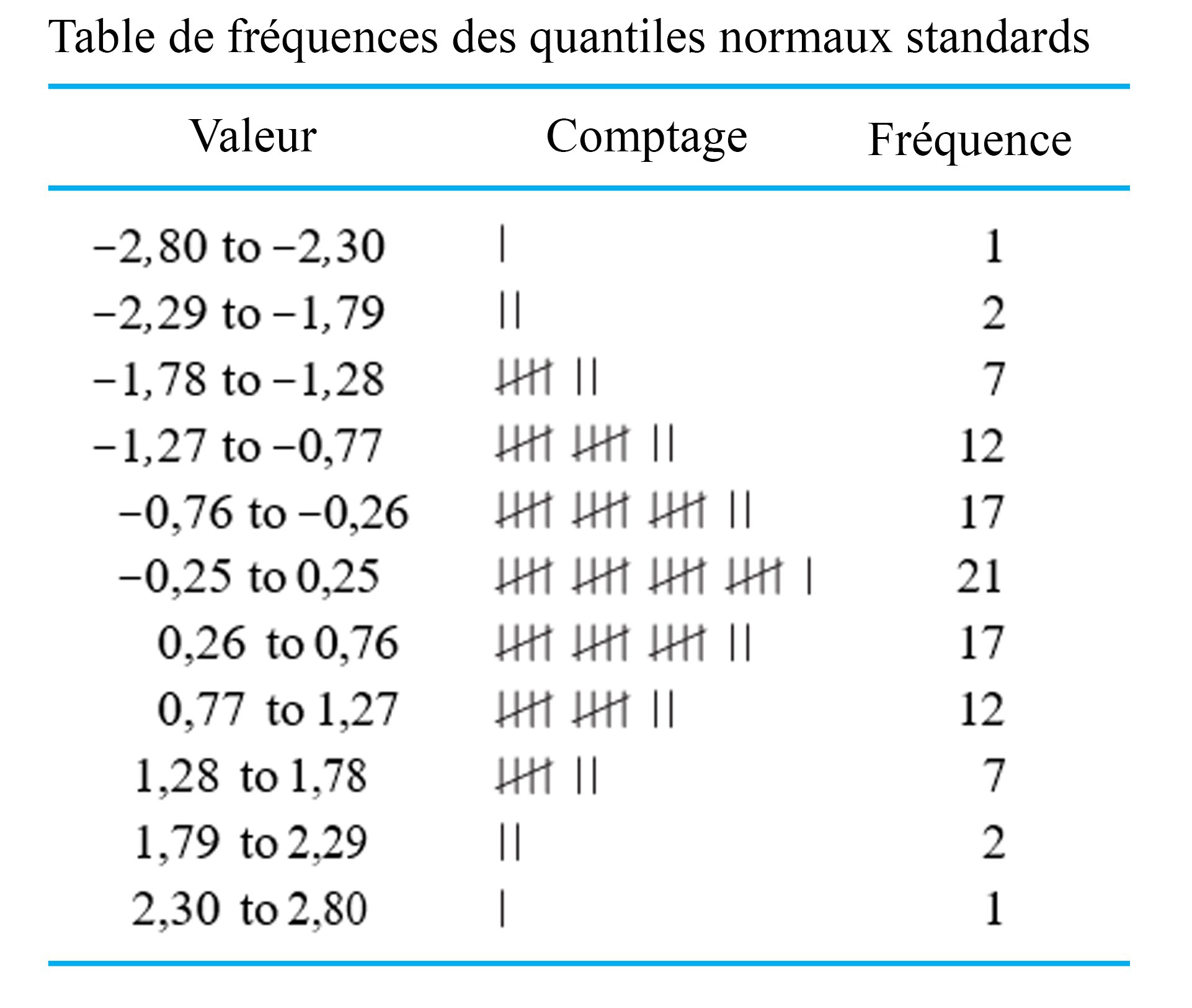
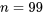 . Le tableau 2.1.7.3 présente une table de fréquences pour ces 99 points de données. La colonne Comptage du tableau 2.1.7.3 montre clairement la forme de cloche.
. Le tableau 2.1.7.3 présente une table de fréquences pour ces 99 points de données. La colonne Comptage du tableau 2.1.7.3 montre clairement la forme de cloche. théorique afin d’évaluer la forme en cloche d’un ensemble de données. Le diagramme obtenu est appelé diagramme normal (de probabilité).
théorique afin d’évaluer la forme en cloche d’un ensemble de données. Le diagramme obtenu est appelé diagramme normal (de probabilité).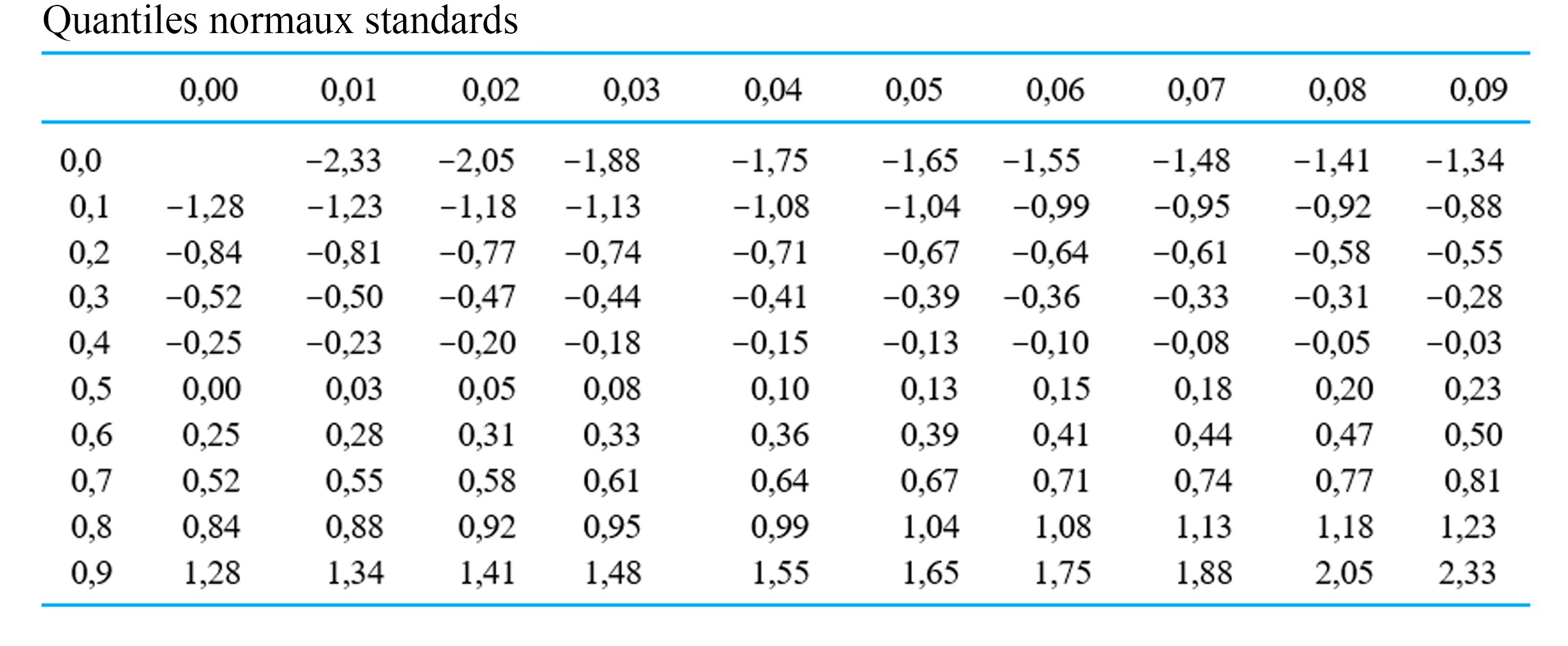
.
Exemple 2.1.7.2. Résistance d’une serviette en papier (suite)
 théorique de la figure 2.1.7.4.
théorique de la figure 2.1.7.4.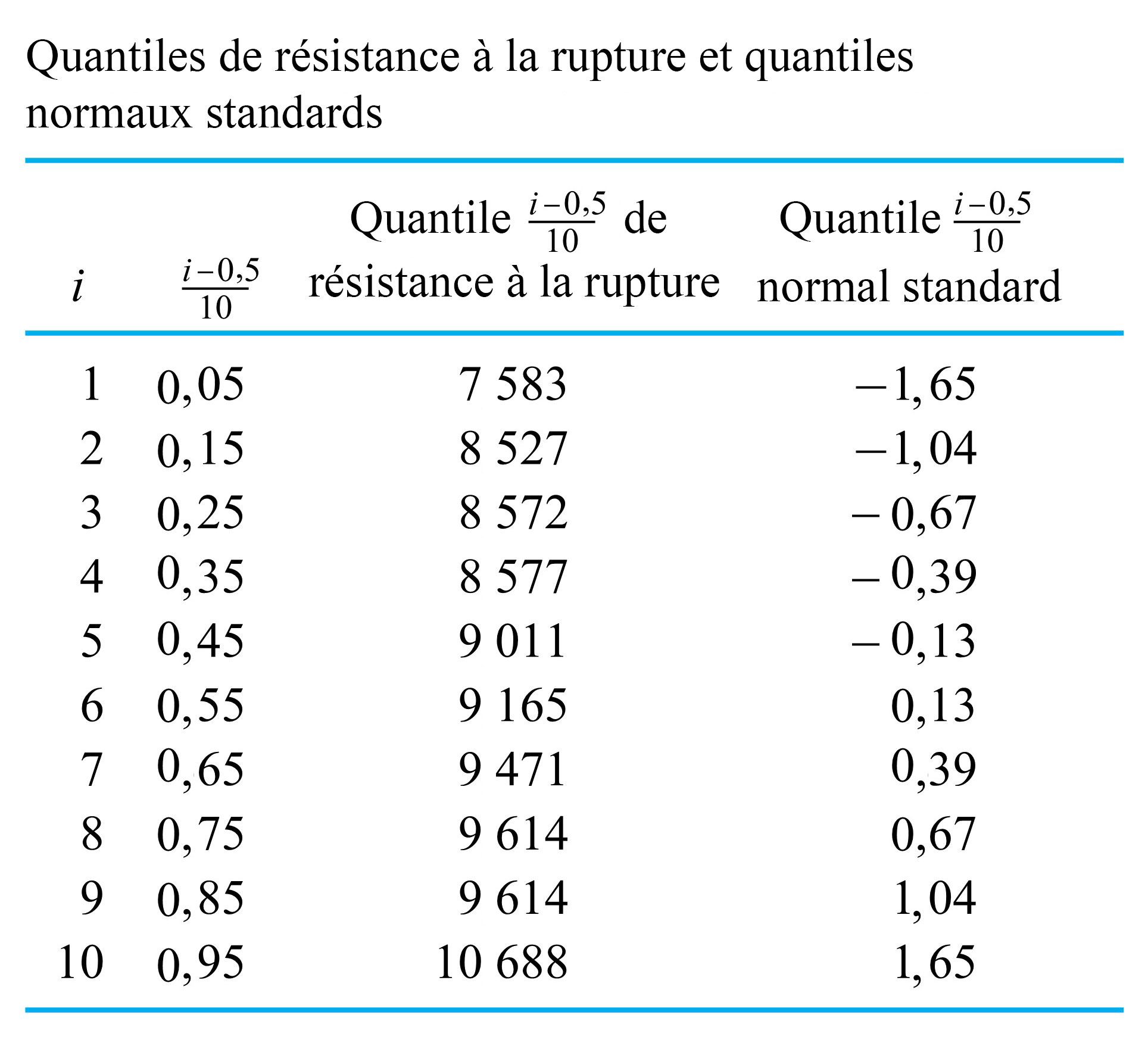
.
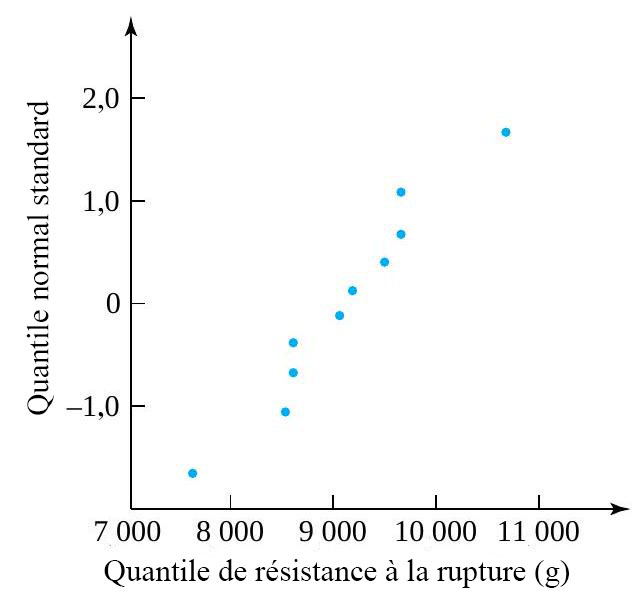
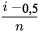 . La figure 2.1.7.4 montre les données de résistance de l’exemple 2.1.7.2 tracées sur du papier de probabilité. À noter que ce tracé est pratiquement identique à celui de la figure 2.1.7.2.
. La figure 2.1.7.4 montre les données de résistance de l’exemple 2.1.7.2 tracées sur du papier de probabilité. À noter que ce tracé est pratiquement identique à celui de la figure 2.1.7.2.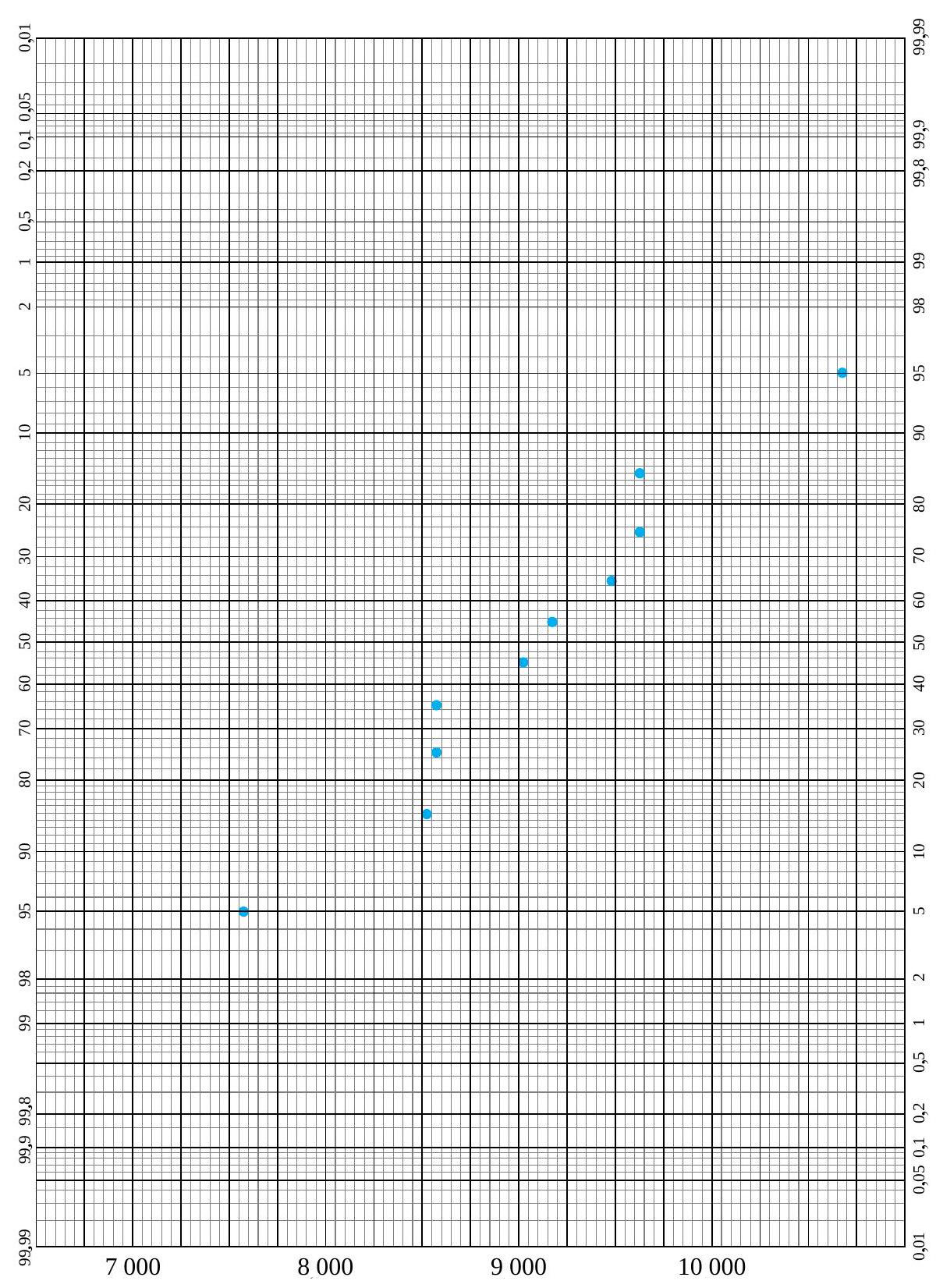
 théoriques utiles en ingénierie. De nombreux autres types de distributions théoriques sont importants, et chacun d’entre eux peut servir à produire des tracés
théoriques utiles en ingénierie. De nombreux autres types de distributions théoriques sont importants, et chacun d’entre eux peut servir à produire des tracés  théoriques. Ce point est abordé plus en détail dans d’autres modules, mais l’introduction du tracé
théoriques. Ce point est abordé plus en détail dans d’autres modules, mais l’introduction du tracé ![permet d’insister sur le lien entre les graphiques de probabilités et les graphiques [latex]Q-Q[/latex] empiriques. Q-Q[/latex]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/e8180ab99492aaee8d689a75d59cbc88.png)