9.3.2 Plan d’expériences : L’approche générale
9.3.4. L’approche générale de la modélisation des surfaces de réponse
- À partir des conditions de référence, on identifie les facteurs principaux en se référant au processus, à des opinions d’experts ou à son intuition. On réalise des expériences factorielles (complètes ou fractionnaires) complètement randomisées. On utilise les résultats de ces expériences pour estimer un modèle linéaire du système :
\[\hat{y} = b_0 + b_Ax_A + b_B x_B + b_C x_C \ldots + b_{AB}x_Ax_B + b_{AC} x_A x_C + \ldots\]
- Les effets principaux sont généralement beaucoup plus importants que les interactions à deux facteurs, de sorte qu’on peut négliger ces termes d’ordre supérieur. Tout effet principal non significatif peut se voir écarté lors d’itérations ultérieures. (Pensez à ce qui a été abordé à la section précédente.)
- On utilise le modèle pour estimer la trajectoire de pente maximale :
\[\dfrac{\partial \hat{y}}{\partial x_1} = b_1 \qquad\qquad \dfrac{\partial \hat{y}}{\partial x_2} = b_2 \qquad \ldots\]
Pour gravir (ou descendre, dans un problème de minimisation) la trajectoire de pente maximale, on déplace n’importe lequel des effets principaux, p. ex. \(b_A\) d’une certaine quantité
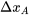 , puis on déplace les autres effets d’un pas
, puis on déplace les autres effets d’un pas 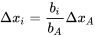 . Par exemple, le pas
. Par exemple, le pas 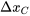 vaut
vaut 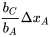 .
.Si l’une des valeurs
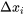 se révèle trop élevée pour être mise en application sans risque, on rapetisse le pas et on applique le même facteur de proportionnalité à tous les autres pas. Rappelez-vous qu’il s’agit d’unités codées; il faut donc appliquer le facteur d’échelle pour obtenir la valeur du déplacement en unités réelles.
se révèle trop élevée pour être mise en application sans risque, on rapetisse le pas et on applique le même facteur de proportionnalité à tous les autres pas. Rappelez-vous qu’il s’agit d’unités codées; il faut donc appliquer le facteur d’échelle pour obtenir la valeur du déplacement en unités réelles. - On répète ce processus jusqu’à ce que la réponse commence à se stabiliser ou que l’on ait la certitude d’être passé à un autre régime du processus.
- À ce stade, on répète l’expérience factorielle à partir de l’étape 1, en utilisant la dernière meilleure valeur de réponse comme nouveau point de référence. C’est aussi le bon moment de réintroduire les termes auparavant négligés. Aussi, dans le cas d’un facteur binaire, on examine l’effet de l’alternance de son signe à cette même étape. Ces expériences factorielles supplémentaires devraient également inclure des points de centrage.
- On répète les étapes 1 à 5 jusqu’à ce que l’estimation du modèle linéaire affiche des signes de courbure ou que les termes d’interaction commencent à dominer les effets principaux. Ceci indique qu’on s’approche d’un optimum.
- On peut évaluer la courbure en comparant le point de centrage prédit, c’est-à-dire le point d’intersection du modèle =
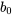 , avec la ou les réponses réelles du point de centrage. Une grande différence entre la prédiction et les effets du modèle indique que la surface de réponse est courbe.
, avec la ou les réponses réelles du point de centrage. Une grande différence entre la prédiction et les effets du modèle indique que la surface de réponse est courbe.
- On peut évaluer la courbure en comparant le point de centrage prédit, c’est-à-dire le point d’intersection du modèle =
- En cas de courbure, on ajoute des points axiaux pour transformer le plan factoriel en plan composite centré. On estime ensuite un modèle quadratique de la forme :
\[y = b_0 + b_1x_1 + b_2 x_2 + \ldots + b_{12}x_1x_2 + \ldots + b_{11}x_1^2 + b_{22}x_2^2 + \ldots\]
- On dessine les tracés de contour de cette surface de réponse estimée et on détermine où positionner les expériences séquentielles. On peut également obtenir l’optimum du modèle de manière analytique en calculant les dérivées de la fonction du modèle.
Résumé
- Dans les sections précédentes, on a utilisé des analyses factorielles complètes ou fractionnaires pour sélectionner les facteurs importants. Au moment de procéder à l’optimisation des processus, on présume que les variables importantes ont déjà été identifiées. En réalité, il arrive que des variables auparavant considérées comme importantes deviennent secondaires à mesure que l’on s’approche de l’optimum. Inversement, des variables qui auraient pu être écartées au départ deviennent importantes à l’optimum.
- En règle générale, la méthode des surfaces de réponse fonctionne mieux lorsque les variables prises en compte sont continues. Les variables de catégorie (oui ou non, catalyseur A ou B) se traitent en les associant à une valeur ou à l’autre, puis en effectuant l’optimisation en fonction de ces valeurs sélectionnées. Il s’avère toujours utile d’examiner les autres valeurs une fois l’optimum atteint.
