L’algèbre matricielle est largement utilisée pour effectuer des régressions multiples, car elle permet de représenter l’analyse de régression de manière compacte et intuitive. Par exemple, un modèle de régression multiple estimé en notion scalaire s’exprime comme suit :

. En utilisant la notation matricielle, la même équation peut être exprimée sous une forme plus compacte et (étonnamment!) plus intuitive :
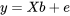
.
.
En plus, la notation matricielle est flexible puisqu’elle peut traiter n’importe quel nombre de variables indépendantes. Les opérations effectuées sur la matrice modélisant
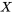
sont réalisées simultanément sur toutes les variables indépendantes. Enfin, vous verrez que l’expression matricielle est largement utilisée dans les présentations statistiques des résultats de l’analyse des MCO. Pour toutes ces raisons, on commence donc par développer la régression multiple sous forme de matrice.
.
Fondements de l’algèbre matricielle
Une matrice est un tableau rectangulaire de nombres disposés en lignes et en colonnes. Comme nous l’avons dit, les opérations effectuées sur les matrices le sont simultanément sur tous les éléments de la matrice. Cette section présentera les notions de base de l’algèbre matricielle nécessaires pour comprendre l’expression de la régression multiple sous forme matricielle.
Fondements des matrices
Les nombres composant une matrice sont appelés « éléments ». Les éléments d’une matrice peuvent être identifiés par leur position dans une ligne et une colonne, désignées par
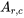
. Dans l’exemple suivant,
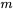
fait référence à la ligne de la matrice et
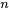
fait référence à la colonne.
.
.
Par conséquent, dans la matrice suivante,
.
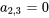
et
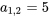
.
.
Vecteurs
Un vecteur est une matrice composée d’une seule colonne ou d’une seule ligne. Par exemple :
.
.
ou
.
Opérations matricielles
Plusieurs « opérations » peuvent être effectuées avec et sur les matrices. La plupart d’entre elles peuvent être calculées à l’aide de Python; nous utiliserons donc cet exemple tout au long du parcours.
Sources
Le contenu des chapitres 8.2.1.1 et 8.2.2.2 est issu de l’ouvrage « Quantitative Research Methods for Political Science, Public Policy and Public Administration : 4th Edition With Applications in R », de Hank Jenkins-Smith, Joseph Ripberger, Gary Copeland, Matthew Nowlin, Tyler Hughes, Aaron Fister, Wesley Wehde, et Josie Davis, consultable à l’adresse https://bookdown.org/ripberjt/qrmbook/. Cet ouvrage est partagé en vertu d’une licence Creative Commons Attribution 4.0 International (CC BY 4.0).
 . En utilisant la notation matricielle, la même équation peut être exprimée sous une forme plus compacte et (étonnamment!) plus intuitive :
. En utilisant la notation matricielle, la même équation peut être exprimée sous une forme plus compacte et (étonnamment!) plus intuitive : 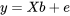 .
.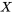 sont réalisées simultanément sur toutes les variables indépendantes. Enfin, vous verrez que l’expression matricielle est largement utilisée dans les présentations statistiques des résultats de l’analyse des MCO. Pour toutes ces raisons, on commence donc par développer la régression multiple sous forme de matrice.
sont réalisées simultanément sur toutes les variables indépendantes. Enfin, vous verrez que l’expression matricielle est largement utilisée dans les présentations statistiques des résultats de l’analyse des MCO. Pour toutes ces raisons, on commence donc par développer la régression multiple sous forme de matrice.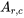 . Dans l’exemple suivant,
. Dans l’exemple suivant, 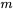 fait référence à la ligne de la matrice et
fait référence à la ligne de la matrice et 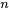 fait référence à la colonne.
fait référence à la colonne.![A_{m, n}=\left[\begin{array}{cccc}a_{1,1} & a_{1,2} & \cdots & a_{1, n} \\ a_{2,1} & a_{2,2} & \cdots & a_{2, n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m, 1} & a_{m, 2} & \cdots & a_{m, n}\end{array}\right] A_{m, n} = \left[\begin{array}{cccc}a_{1,1} & a_{1,2} & \cdots & a_{1, n} \\ a_{2,1} & a_{2,2} & \cdots & a_{2, n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m, 1} & a_{m, 2} & \cdots & a_{m, n}\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/3687c16872bfd24c0ad12d35fda788d4.png)
![A = \left[\begin{array}{ccc}10 & 5 & 8 \\ -12 & 1 & 0\end{array}\right] A = \left[\begin{array}{ccc}10 & 5 & 8 \\ -12 & 1 & 0\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/97f9b7e52dcadce020e355199f5bc568.png)
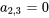 et
et 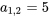 .
.![A = \left[\begin{array}{c}6 \\ -1 \\ 8 \\ 11\end{array}\right] A = \left[\begin{array}{c}6 \\ -1 \\ 8 \\ 11\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/d867c8d8d16e69976327c05841eefb79.png)
![A = \left[\begin{array}{llll}1 & 2 & 8 & 7\end{array}\right] A = \left[\begin{array}{llll}1 & 2 & 8 & 7\end{array}\right]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/3b9e4aa30734805efc2dd0f148386a02.png)
