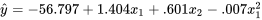8.1.6 Quelques précautions additionnelles : extrapolation, valeurs aberrantes et parcimonie
Extrapolation
 . On peut raisonnablement compter sur une équation ajustée pour décrire la relation entre
. On peut raisonnablement compter sur une équation ajustée pour décrire la relation entre  et un ensemble particulier de valeurs de
et un ensemble particulier de valeurs de 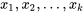 uniquement si ces valeurs sont semblables à celles utilisés pour créer l’équation. L’ajustement de surface présente un défi :
uniquement si ces valeurs sont semblables à celles utilisés pour créer l’équation. L’ajustement de surface présente un défi :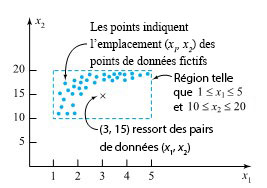
.
L’influence des vecteurs de données aberrantes
L’ajustement des courbes et des surfaces par les moindres carrés peut être fortement affecté par quelques données aberrantes ou extrêmes, ce qui constitue un autre piège potentiel. On peut essayer de déceler ces points en examinant les graphiques et en comparant les ajustements réalisés avec et sans le ou les points suspects.
Exemple 8.1.6.1 Données sur la perte dans la cheminée (suite)
 extrême. La figure 8.1.6.2 est un nuage de points des paires
extrême. La figure 8.1.6.2 est un nuage de points des paires 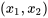 pour les données du tableau 8.1.3.1. Elle montre que, selon la plupart des normes qualitatives, l’observation 1 du tableau 8.1.3.1 est inhabituelle ou aberrante.
pour les données du tableau 8.1.3.1. Elle montre que, selon la plupart des normes qualitatives, l’observation 1 du tableau 8.1.3.1 est inhabituelle ou aberrante.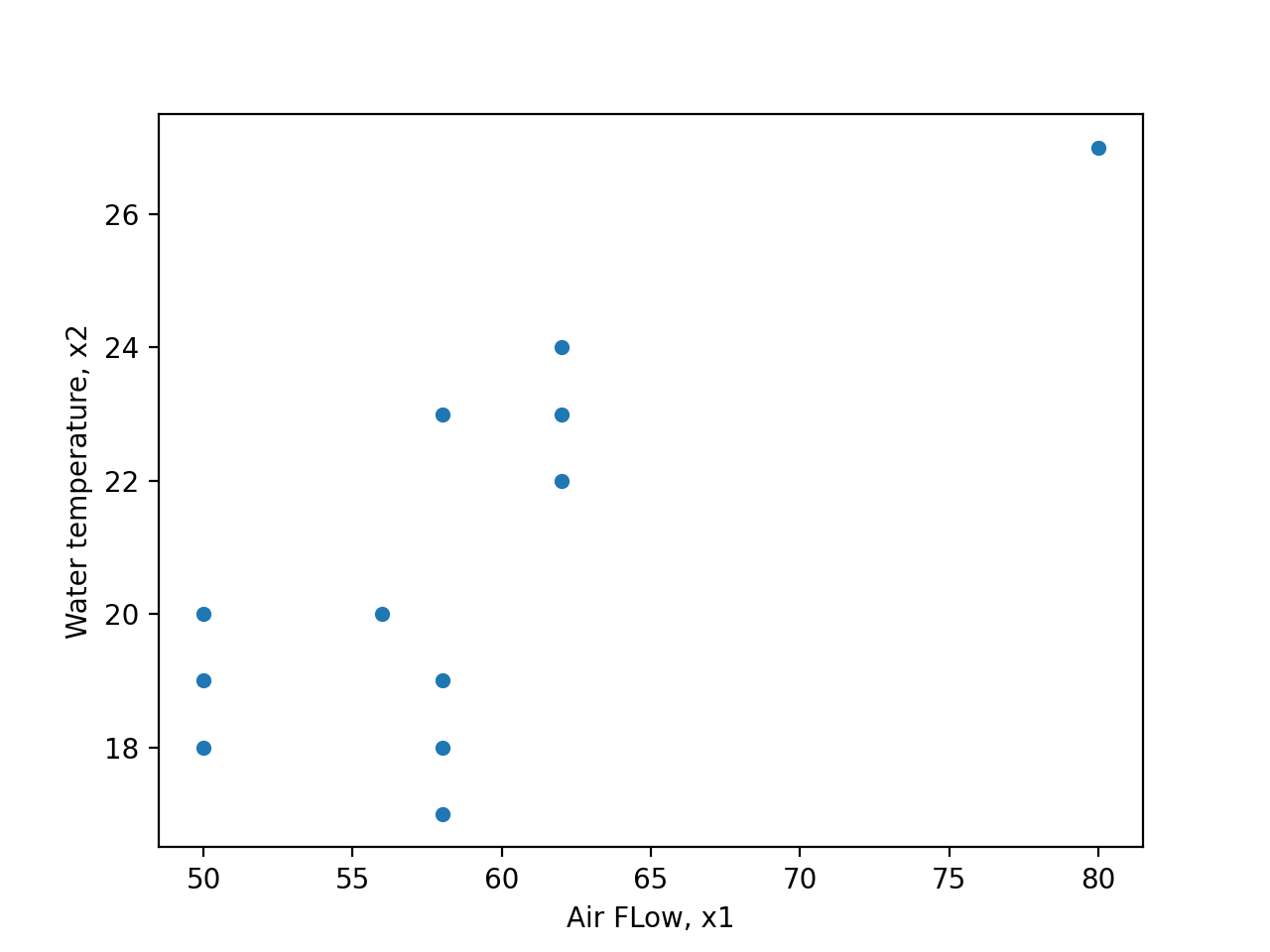
8.1.6.1
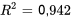 . On pourrait envisager d’utiliser l’équation 8.1.6.1 pour prédire les pertes dans la cheminée et de limiter l’attention à
. On pourrait envisager d’utiliser l’équation 8.1.6.1 pour prédire les pertes dans la cheminée et de limiter l’attention à  dans l’étendue de 50 à 62. Il est toutefois possible de vérifier que, même si certains des coefficients (les
dans l’étendue de 50 à 62. Il est toutefois possible de vérifier que, même si certains des coefficients (les  ) des équations 8.1.3.4 et 8.1.6.1 diffèrent considérablement, les deux équations produisent des valeurs de
) des équations 8.1.3.4 et 8.1.6.1 diffèrent considérablement, les deux équations produisent des valeurs de 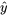 comparables pour les 16 points de données pour lesquels
comparables pour les 16 points de données pour lesquels  se situe entre 50 et 62. En fait, la plus grande différence entre les valeurs ajustées est d’environ 0,4. Par conséquent, étant donné que le point 1 du tableau 8.1.3.1 ne modifie pas radicalement les prédictions faites à l’aide de l’équation ajustée, il est logique de le garder, d’adopter l’équation (8.1.3.4) et de l’utiliser pour décrire les pertes dans la cheminée pour les paires
se situe entre 50 et 62. En fait, la plus grande différence entre les valeurs ajustées est d’environ 0,4. Par conséquent, étant donné que le point 1 du tableau 8.1.3.1 ne modifie pas radicalement les prédictions faites à l’aide de l’équation ajustée, il est logique de le garder, d’adopter l’équation (8.1.3.4) et de l’utiliser pour décrire les pertes dans la cheminée pour les paires 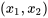 à l’intérieur du modèle de dispersion de la figure 8.1.6.2.
à l’intérieur du modèle de dispersion de la figure 8.1.6.2.Le risque de surajustement
Il faut également souligner que la notion de simplicité (parcimonie) de l’équation n’est pas seulement importante pour des raisons de simplicité d’interprétation et de réduction des coûts liés à l’utilisation de l’équation. Elle est également importante dans la mesure où elle permet d’obtenir une interpolation régulière tout en évitant de surajuster un ensemble de données. Prenons l’exemple de données artificielles, généralement linéaires 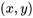 . On pourrait trouver un polynôme de degré
. On pourrait trouver un polynôme de degré 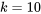 à travers chacun de ces points. Mais dans la plupart des problèmes physiques, une telle courbe serait beaucoup moins efficace pour prédire les valeurs de
à travers chacun de ces points. Mais dans la plupart des problèmes physiques, une telle courbe serait beaucoup moins efficace pour prédire les valeurs de  correspondant à d’autres valeurs de
correspondant à d’autres valeurs de  qu’une simple ligne ajustée. Un polynôme du 10e degré serait surajusté.
qu’une simple ligne ajustée. Un polynôme du 10e degré serait surajusté.
Modèles empiriques et ingénierie
Pour conclure cette section, examinons comment les méthodes abordées ici s’inscrivent dans le cadre général de l’utilisation de modèles pour résoudre des problèmes d’ingénierie. Il faut reconnaître que les théories de la physique, de la chimie, des matériaux, etc. produisent rarement des équations des formes simples présentées ici. Parfois, des équations pertinentes de ces théories peuvent être réécrites sous ces formes, comme dans le cas de l’équation de Taylor pour la durée de vie des outils, présentée précédemment dans cette section. Mais la majorité des applications d’ingénierie des méthodes de cette section concernent la foule de problèmes pour lesquels il n’existe pas de théorie physique simple et bien connue, et pour lesquels une simple description empirique de la situation serait utile. Dans de tels cas, l’ajustement des courbes et des surfaces par les moindres carrés peut offrir un aperçu ou une estimation éclairée permettant d’établir des descriptions empiriques approximatives de la relation entre une réponse  et les variables d’entrée du système
et les variables d’entrée du système 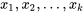 .
.