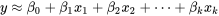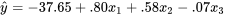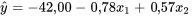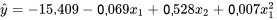8.1.3 Ajustement des surfaces par les moindres carrés
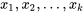 sur une réponse
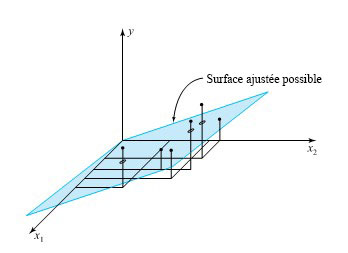
sur une réponse  . D’un point de vue géométrique, le problème consiste à effectuer une régression avec une équation du type
. D’un point de vue géométrique, le problème consiste à effectuer une régression avec une équation du type8.1.3.1
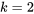 , avec six points de données
, avec six points de données 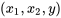 et une surface d’ajustement possible de la forme 8.1.3.1. Pour faire la régression d’un ensemble de
et une surface d’ajustement possible de la forme 8.1.3.1. Pour faire la régression d’un ensemble de 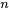 points de données
points de données  avec une équation de la forme 8.1.3.1 en utilisant la méthode des moindres carrés, il faut minimiser la fonction de
avec une équation de la forme 8.1.3.1 en utilisant la méthode des moindres carrés, il faut minimiser la fonction de 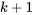 variables
variables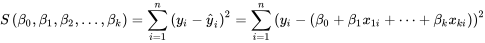
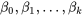 . En mettant les dérivées partielles par rapport aux coefficients
. En mettant les dérivées partielles par rapport aux coefficients 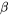 égales à 0, on obtient des équations normales, généralisant ainsi les équations de régression linéaire. La résolution de ces
égales à 0, on obtient des équations normales, généralisant ainsi les équations de régression linéaire. La résolution de ces 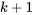 équations linéaires à
équations linéaires à 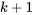 inconnues
inconnues 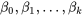 constitue la première étape d’une régression linéaire multiple. Les coefficients de régression
constitue la première étape d’une régression linéaire multiple. Les coefficients de régression 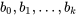 qui en sont issus minimisent
qui en sont issus minimisent 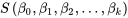 .
.
.
Exemple 8.1.3.1 Ajustement par une surface et données de Brownlee sur les pertes dans la cheminée
 , correspond au taux de fonctionnement de l’installation. La variable de concentration en acide,
, correspond au taux de fonctionnement de l’installation. La variable de concentration en acide, 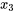 , correspond au pourcentage en circulation moins 50, multiplié par 10. La variable de réponse,
, correspond au pourcentage en circulation moins 50, multiplié par 10. La variable de réponse,  , correspond à 10 fois le pourcentage d’ammoniac entrant qui s’échappe de la cheminée sans être absorbé (essentiellement, c’est une mesure inverse de l’efficacité globale de l’installation). Afin de comprendre, prévoir, et si possible optimiser les performances de l’usine, il serait utile d’avoir une équation décrivant la manière dont
, correspond à 10 fois le pourcentage d’ammoniac entrant qui s’échappe de la cheminée sans être absorbé (essentiellement, c’est une mesure inverse de l’efficacité globale de l’installation). Afin de comprendre, prévoir, et si possible optimiser les performances de l’usine, il serait utile d’avoir une équation décrivant la manière dont  dépend de
dépend de 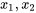 , et
, et 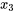 . L’ajustement des surfaces par les moindres carrés constitue une méthode pour obtenir ce type d’équation empirique.
. L’ajustement des surfaces par les moindres carrés constitue une méthode pour obtenir ce type d’équation empirique.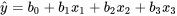
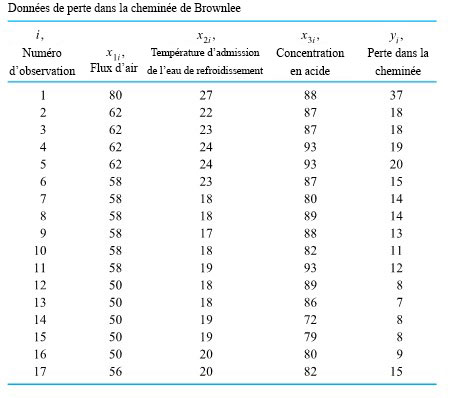
.
8.1.3.2
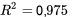 . Les coefficients de cette équation peuvent être vus comme le taux de variation des pertes dans la cheminée en fonction des variables individuelles
. Les coefficients de cette équation peuvent être vus comme le taux de variation des pertes dans la cheminée en fonction des variables individuelles 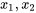 , et
, et 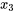 , si on garde les autres variables constantes. Par exemple,
, si on garde les autres variables constantes. Par exemple, 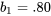 représente l’augmentation des pertes dans la colonne
représente l’augmentation des pertes dans la colonne  qui accompagne une augmentation de flux d’air
qui accompagne une augmentation de flux d’air  d’une unité si la température de l’eau
d’une unité si la température de l’eau 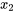 et la concentration en acide
et la concentration en acide 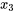 sont constantes. Les signes des coefficients indiquent si
sont constantes. Les signes des coefficients indiquent si  tend à augmenter ou à diminuer avec l’augmentation des valeurs de
tend à augmenter ou à diminuer avec l’augmentation des valeurs de  correspondantes. Par exemple, le fait que
correspondantes. Par exemple, le fait que 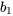 soit positif indique que plus l’usine fonctionne à un rythme élevé, plus
soit positif indique que plus l’usine fonctionne à un rythme élevé, plus  tend à avoir une valeur élevée (ce qui signifie que l’usine fonctionne de manière moins efficace). La valeur importante de
tend à avoir une valeur élevée (ce qui signifie que l’usine fonctionne de manière moins efficace). La valeur importante de 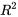 est un premier indicateur de l’efficacité de l’équation 8.1.3.2 pour représenter les données.
est un premier indicateur de l’efficacité de l’équation 8.1.3.2 pour représenter les données.cheminée = -37,65 + 0,80 air + 0,58 eau + -0,07 acide.
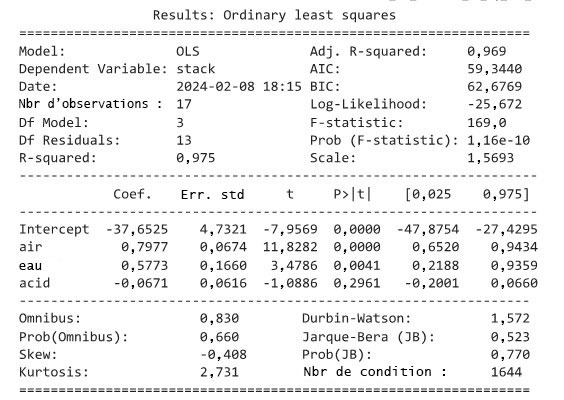
.

Objectif de la régression multiple
Bien que les techniques de régression de données à plusieurs variables au moyen d’équations de la forme 8.1.3.1 soient relativement simples, le choix et l’interprétation des équations appropriées ne sont pas aussi évidents. Lorsqu’un grand nombre de variables  sont prises en compte, le nombre d’équations potentielles de la forme 8.1.3.1 est considérable. Et pour ne rien arranger, il n’existe pas de méthode totalement satisfaisante pour représenter graphiquement plusieurs variables
sont prises en compte, le nombre d’équations potentielles de la forme 8.1.3.1 est considérable. Et pour ne rien arranger, il n’existe pas de méthode totalement satisfaisante pour représenter graphiquement plusieurs variables  et « voir » la qualité de la régression. Tout ce que nous pouvons faire à ce stade est d’offrir le conseil général de rechercher l’équation de régression la plus simple permettant un ajustement adéquat aux données, puis de fournir des exemples de la manière dont
et « voir » la qualité de la régression. Tout ce que nous pouvons faire à ce stade est d’offrir le conseil général de rechercher l’équation de régression la plus simple permettant un ajustement adéquat aux données, puis de fournir des exemples de la manière dont 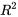 et le tracé des résidus peuvent constituer des outils utiles pour résoudre les difficultés qui se présentent.
et le tracé des résidus peuvent constituer des outils utiles pour résoudre les difficultés qui se présentent.
Exemple 8.1.3.2 (suite)
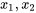 , et
, et 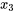 , sont nécessaires pour représenter de manière adéquate la variation de
, sont nécessaires pour représenter de manière adéquate la variation de  observée. Par exemple, l’évolution des pertes dans la cheminée pourrait être expliquée de manière appropriée en utilisant uniquement une ou deux des trois variables
observée. Par exemple, l’évolution des pertes dans la cheminée pourrait être expliquée de manière appropriée en utilisant uniquement une ou deux des trois variables  . Cela aurait plusieurs conséquences pratiques importantes en matière d’ingénierie. Premièrement, dans un tel cas, le processus d’oxydation pourrait être décrit au moyen d’une version simple ou parcimonieuse de l’équation 8.1.3.1. Et si une variable ne s’avère pas nécessaire pour prédire
. Cela aurait plusieurs conséquences pratiques importantes en matière d’ingénierie. Premièrement, dans un tel cas, le processus d’oxydation pourrait être décrit au moyen d’une version simple ou parcimonieuse de l’équation 8.1.3.1. Et si une variable ne s’avère pas nécessaire pour prédire  , alors des économies liées à sa mesure peuvent être réalisées. Ou alors, si une variable ne semble pas avoir de réel impact sur
, alors des économies liées à sa mesure peuvent être réalisées. Ou alors, si une variable ne semble pas avoir de réel impact sur  (parce qu’il ne paraît pas essentiel de l’inclure dans l’équation décrivant le comportement de
(parce qu’il ne paraît pas essentiel de l’inclure dans l’équation décrivant le comportement de  ), il doit être possible de l’ajuster pour des motifs purement économiques, sans crainte de dégrader l’efficacité du processus.
), il doit être possible de l’ajuster pour des motifs purement économiques, sans crainte de dégrader l’efficacité du processus.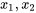 , et
, et 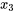 permet effectivement d’expliquer le comportement des pertes dans la cheminée, des valeurs de
permet effectivement d’expliquer le comportement des pertes dans la cheminée, des valeurs de 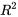 ont été calculées pour les équations basées sur tous les sous-ensembles possibles de
ont été calculées pour les équations basées sur tous les sous-ensembles possibles de 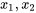 et
et 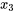 , et elles ont été regroupées dans le tableau 8.1.3.2. Ce tableau montre que, par exemple,
, et elles ont été regroupées dans le tableau 8.1.3.2. Ce tableau montre que, par exemple, 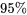 de la variabilité totale en
de la variabilité totale en  peut être prise en compte à l’aide d’une équation linéaire comprenant uniquement la variable de débit d’air
peut être prise en compte à l’aide d’une équation linéaire comprenant uniquement la variable de débit d’air  . L’utilisation de
. L’utilisation de  et de la variable de température de l’eau
et de la variable de température de l’eau 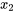 permet de rendre compte de
permet de rendre compte de 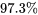 de la variabilité totale des pertes dans la cheminée. Inclure
de la variabilité totale des pertes dans la cheminée. Inclure 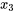 , la variable de concentration en acide, dans une équation comprenant déjà
, la variable de concentration en acide, dans une équation comprenant déjà  et
et 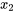 , ne fait passer la valeur de
, ne fait passer la valeur de 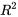 que de 0,973 à 0,975.
que de 0,973 à 0,975.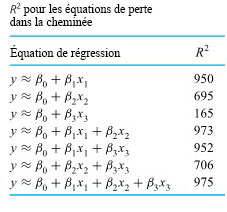
 , puis éventuellement de
, puis éventuellement de 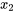 . À la lumière de ces valeurs de
. À la lumière de ces valeurs de 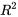 , il semble inutile d’inclure un terme en
, il semble inutile d’inclure un terme en 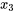 dans l’équation de
dans l’équation de  . Rétrospectivement, ceci est tout à fait cohérent avec le comportement de l’équation de régression 8.1.3.1 :
. Rétrospectivement, ceci est tout à fait cohérent avec le comportement de l’équation de régression 8.1.3.1 : 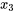 varie entre 72 et 93 dans la série de données originale, ce qui signifie que la valeur de
varie entre 72 et 93 dans la série de données originale, ce qui signifie que la valeur de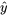 n’évolue globalement que de
n’évolue globalement que de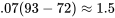
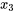 . (Il faut se rappeler que
. (Il faut se rappeler que 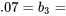 pente de
pente de  en fonction de
en fonction de 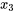 dans l’équation de régression.) Une valeur de 1,5 est relativement peu élevée comparée à la plage des valeurs de
dans l’équation de régression.) Une valeur de 1,5 est relativement peu élevée comparée à la plage des valeurs de  observées.
observées.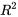 ont été utilisées pour identifier les simplifications possibles de l’équation
ont été utilisées pour identifier les simplifications possibles de l’équation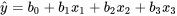
elles peuvent et doivent être intégrées à une analyse approfondie des résidus, avant d’être validées en tant que données de synthèse. À titre d’exemple, considérons une équation de régression en  et
et 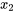 . Un programme de régression linéaire multiple peut être utilisé pour produire l’équation de régression suivante :
. Un programme de régression linéaire multiple peut être utilisé pour produire l’équation de régression suivante :
8.1.3.3
(Il faut noter que les valeurs de 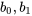 , et
, et 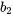 de l’équation 8.1.3.3 diffèrent légèrement des valeurs de l’équation 8.1.3.2. En effet, l’équation 8.1.3.3 n’a pas été obtenue
de l’équation 8.1.3.3 diffèrent légèrement des valeurs de l’équation 8.1.3.2. En effet, l’équation 8.1.3.3 n’a pas été obtenue
 changent en fonction des variables
changent en fonction des variables  qui sont incluses ou non dans la régression.)
qui sont incluses ou non dans la régression.)Les résidus issus de l’équation 8.1.3.3 peuvent être calculés et représentés de différentes manières potentiellement utiles. La figure 8.1.3.2 présente un graphique normal des résidus et trois autres graphiques des résidus en fonction de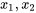 , et
, et 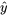 , respectivement. Les graphiques de la figure 8.1.3.2 n’apportent pas d’information très significative, sauf peut-être que l’ensemble de données présente une valeur de
, respectivement. Les graphiques de la figure 8.1.3.2 n’apportent pas d’information très significative, sauf peut-être que l’ensemble de données présente une valeur de  inhabituellement élevée ainsi qu’une valeur de
inhabituellement élevée ainsi qu’une valeur de 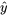 inhabituellement élevée (qui elle-même correspond à la valeur élevée de
inhabituellement élevée (qui elle-même correspond à la valeur élevée de  ). Toutefois, le tracé des résidus en fonction de
). Toutefois, le tracé des résidus en fonction de  présente une configuration curviligne « croissante-décroissante-croissante » permettant de suggérer l’ajout d’un terme en
présente une configuration curviligne « croissante-décroissante-croissante » permettant de suggérer l’ajout d’un terme en 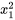 à l’équation de régression 8.1.3.3.
à l’équation de régression 8.1.3.3.
.
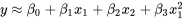
8.1.3.4
avec 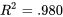 et des résidus présentant une tendance encore moins marquée que ceux de l’équation de régression 8.1.3.3. Et on remarquera que le signe d’une courbure identifié sur le graphique des résidus en fonction de
et des résidus présentant une tendance encore moins marquée que ceux de l’équation de régression 8.1.3.3. Et on remarquera que le signe d’une courbure identifié sur le graphique des résidus en fonction de  pour l’équation 8.1.3.3 n’apparaît pas sur le graphique équivalent pour l’équation 8.1.3.4. Il est intéressant de noter, à travers cet exemple, que l’équation de régression 8.1.3.4 présente une meilleure valeur
pour l’équation 8.1.3.3 n’apparaît pas sur le graphique équivalent pour l’équation 8.1.3.4. Il est intéressant de noter, à travers cet exemple, que l’équation de régression 8.1.3.4 présente une meilleure valeur 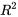 que l’équation de régression 8.1.3.2, malgré le fait que l’équation 8.1.3.2 implique la variable de processus
que l’équation de régression 8.1.3.2, malgré le fait que l’équation 8.1.3.2 implique la variable de processus ![x_ [latex][/latex] et pas l’équation 8.1.3.4.... Figure 8.1.3.2 Graphique des résidus issus d’une équation de régression à deux variables pour les données des pertes dans la colonne d’extraction ( yˆ =−42,00 − 0,78x1 + 0,57x2 ).... L’équation 8.1.3.4 est un peu plus complexe que l’équation 8.1.3.3. Mais parce qu’elle n’implique toujours que deux variables d’entrée [latex][/latex]x](https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/ed657e623bc7ec07e86af658216b93a0.png) width= »546″ height= »454″ /> Figure 8.1.3.2 Plots of residuals from a two-variable equation fit to the stack loss data ( yˆ =−42.00 − .78×1 + .57×2 )[/caption] . Equation (8.1.3.4) is somewhat more complicated than equation (8.1.3.3). But because it still really only involves two different input [latex][/latex]x" class="latex mathjax"></div> </div> <div>.</div> <div><img class="wp-image-450 size-full" src="https://ecampusontario.pressbooks.pub/app/uploads/sites/4023/2024/02/120_1.jpg" alt="" width="546" height="454" /> Figure 8.1.3.2 Plots of residuals from a two-variable equation fit to the stack loss data ( yˆ =−42.00 − .78x1 + .57x2 )et qu’elle élimine également la légère tendance observée sur le graphique des résidus de l’équation 8.1.3.3 en fonction de
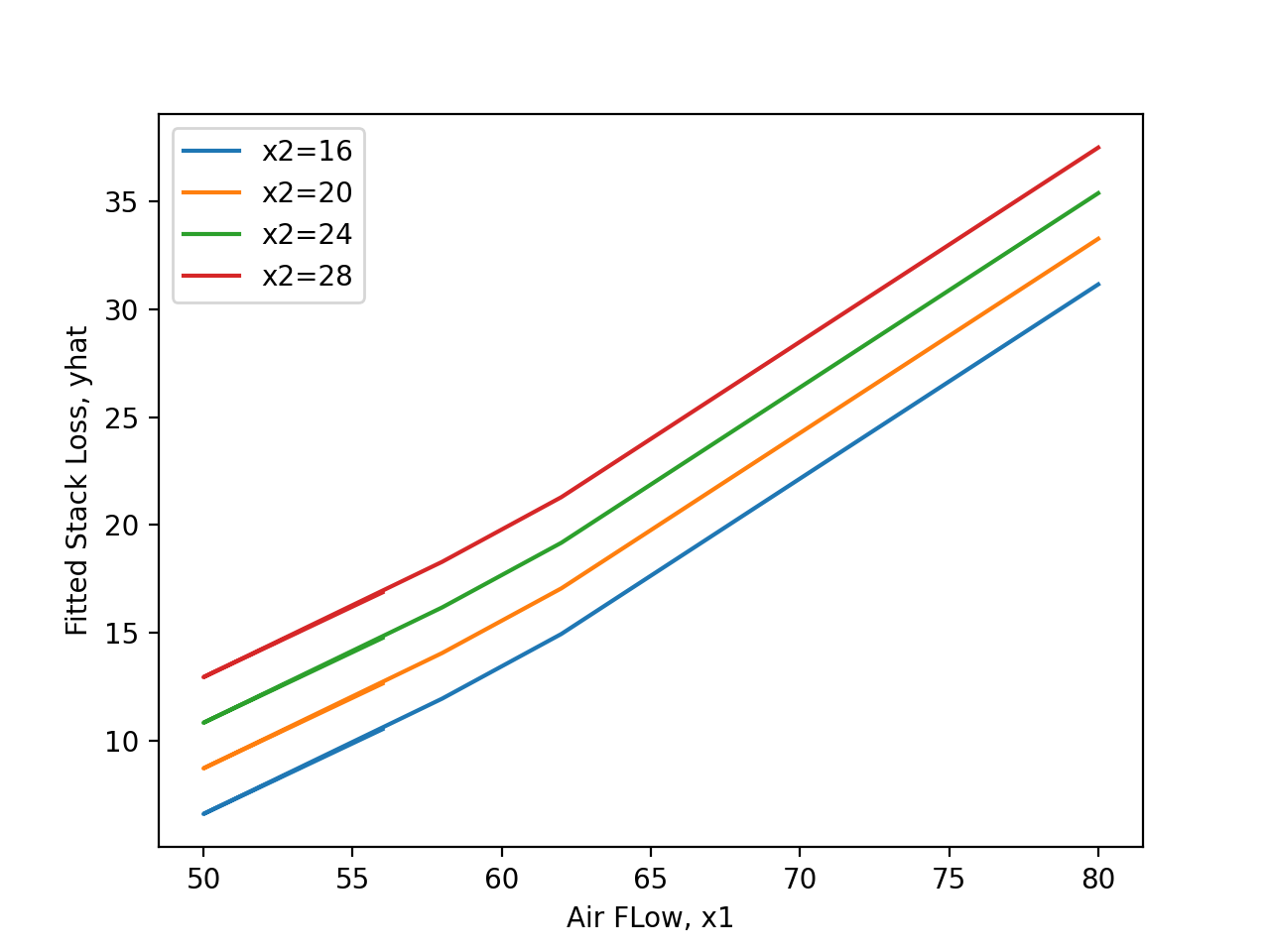
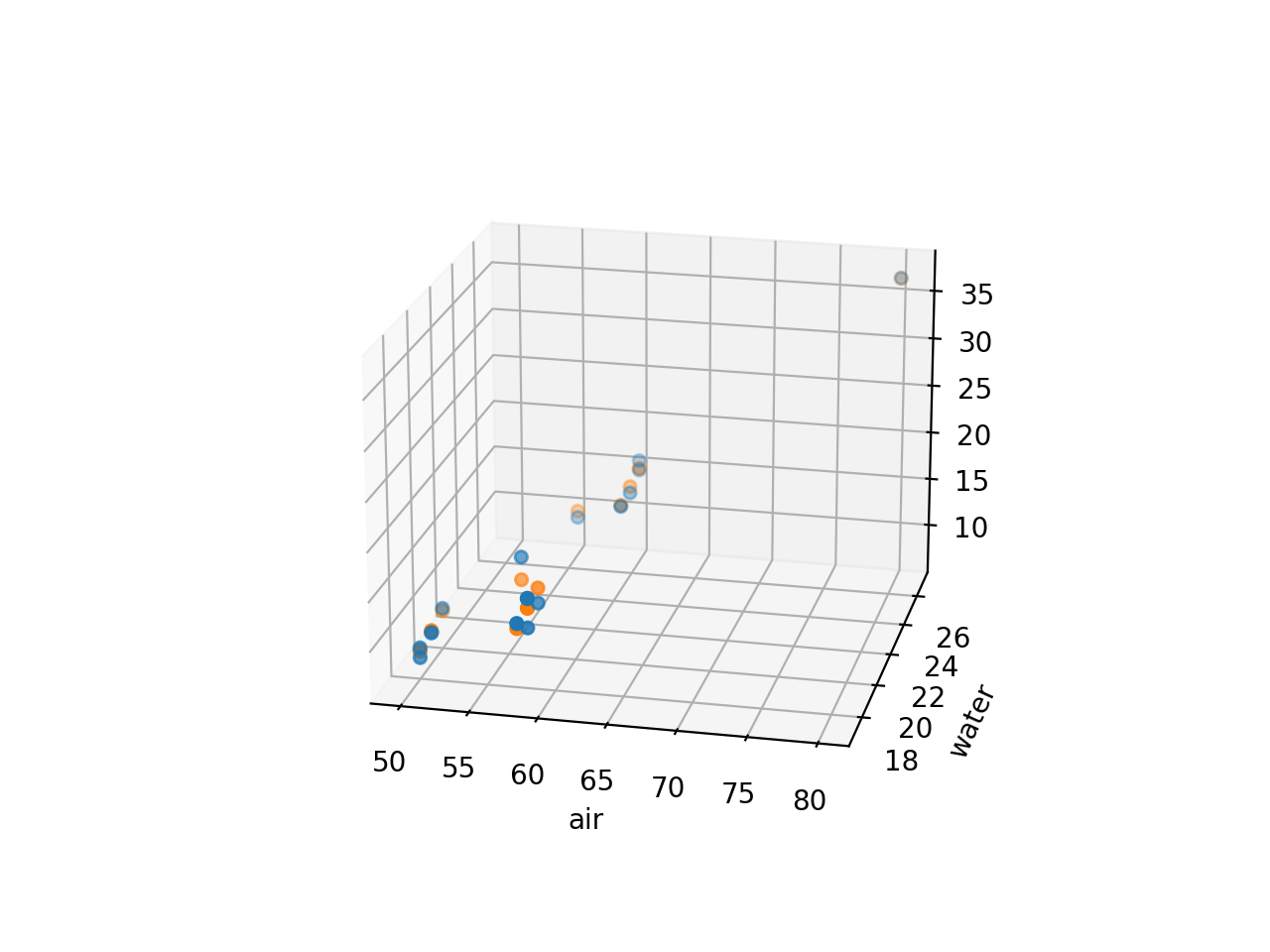
width= »546″ height= »454″ /> Figure 8.1.3.2 Plots of residuals from a two-variable equation fit to the stack loss data ( yˆ =−42.00 − .78×1 + .57×2 )[/caption] . Equation (8.1.3.4) is somewhat more complicated than equation (8.1.3.3). But because it still really only involves two different input [latex][/latex]x" class="latex mathjax"></div> </div> <div>.</div> <div><img class="wp-image-450 size-full" src="https://ecampusontario.pressbooks.pub/app/uploads/sites/4023/2024/02/120_1.jpg" alt="" width="546" height="454" /> Figure 8.1.3.2 Plots of residuals from a two-variable equation fit to the stack loss data ( yˆ =−42.00 − .78x1 + .57x2 )et qu’elle élimine également la légère tendance observée sur le graphique des résidus de l’équation 8.1.3.3 en fonction de  , elle semble être un choix intéressant pour présenter une synthèse des données sur les pertes dans la cheminée. La figure 8.1.3.3 présente un nuage de points 3D des valeurs x1 et x2 issues de l’équation de régression 8.1.3.4. La figure 8.1.3.4 présente une vue 2D de la surface d’ajustement définie par l’équation 8.1.3.4. La légère courbure du tracé résulte du terme en
, elle semble être un choix intéressant pour présenter une synthèse des données sur les pertes dans la cheminée. La figure 8.1.3.3 présente un nuage de points 3D des valeurs x1 et x2 issues de l’équation de régression 8.1.3.4. La figure 8.1.3.4 présente une vue 2D de la surface d’ajustement définie par l’équation 8.1.3.4. La légère courbure du tracé résulte du terme en 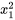 qui apparaît dans l’équation 8.1.3.4. Étant donné que
qui apparaît dans l’équation 8.1.3.4. Étant donné que  varie entre 50 et 62 et
varie entre 50 et 62 et 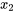 varie entre 17 et 24 pour la majorité des données, le graphique démontre que sur ces plages de valeurs,
varie entre 17 et 24 pour la majorité des données, le graphique démontre que sur ces plages de valeurs,  semble influencer les pertes dans la cheminée davantage que
semble influencer les pertes dans la cheminée davantage que 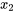 . Cette conclusion est cohérente avec la réflexion menée autour du tableau 8.1.3.2.
. Cette conclusion est cohérente avec la réflexion menée autour du tableau 8.1.3.2.
.