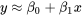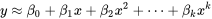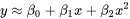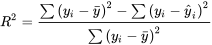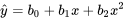8.1.1 Ajustement des courbes par les moindres carrés
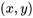 . À titre d’exemple, une étude sera menée pour trouver une équation plus pertinente pour décrire les données relatives au béton de cendres volantes.
. À titre d’exemple, une étude sera menée pour trouver une équation plus pertinente pour décrire les données relatives au béton de cendres volantes.8.1.1.1
8.1.1.2
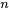 paires est conceptuellement à peine plus difficile que l’ajustement de l’équation 8.1.1.1. La fonction de
paires est conceptuellement à peine plus difficile que l’ajustement de l’équation 8.1.1.1. La fonction de 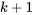 variables
variables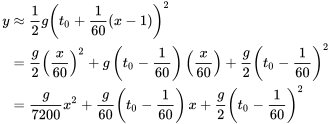
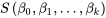 égales à 0, on obtient l’ensemble des équations normales pour ce problème des moindres carrés, généralisant ainsi la paire d’équations de la partie 7.1. Il existe
égales à 0, on obtient l’ensemble des équations normales pour ce problème des moindres carrés, généralisant ainsi la paire d’équations de la partie 7.1. Il existe 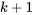 équations linéaires avec
équations linéaires avec 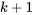 inconnues
inconnues 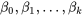 . Généralement, il existe un ensemble de solutions unique
. Généralement, il existe un ensemble de solutions unique 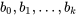 , qui minimise
, qui minimise 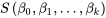 .
.Exemple 8.1.1.1 Retour sur les données de cendres volantes
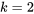 :
:8.1.1.3
 et
et  du tableau 8.1.1.2 en deux colonnes dans le data frame, une colonne supplémentaire a été créée en élevant les valeurs de
du tableau 8.1.1.2 en deux colonnes dans le data frame, une colonne supplémentaire a été créée en élevant les valeurs de  au carré, créant ainsi la variable x_sqr). Ce Jupyter Notebook basé sur le langage Python est disponible sur le site GitHub du cours.
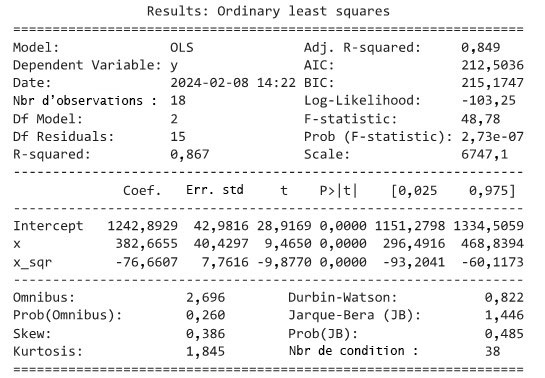
au carré, créant ainsi la variable x_sqr). Ce Jupyter Notebook basé sur le langage Python est disponible sur le site GitHub du cours.L’équation de régression est y = 1,243e+03 + 382,7 x + -76,66 x_sqr
.

.
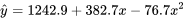
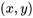 . Bien que la parabole ne soit pas représentative des données de Roth d’une manière tout à fait satisfaisante, elle suit beaucoup mieux la tendance des données que la droite tracée précédemment.
. Bien que la parabole ne soit pas représentative des données de Roth d’une manière tout à fait satisfaisante, elle suit beaucoup mieux la tendance des données que la droite tracée précédemment.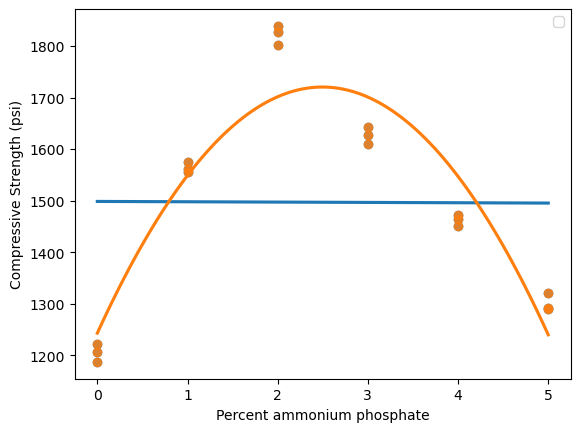
.
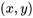 par une droite, il est utile de quantifier la qualité de la régression linéaire au moyen de
par une droite, il est utile de quantifier la qualité de la régression linéaire au moyen de 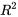 . On peut aussi utiliser le coefficient de détermination lors d’une régression avec un polynôme de la forme de l’équation 8.1.1.2. Rappelons une fois de plus que selon la définition 3,
. On peut aussi utiliser le coefficient de détermination lors d’une régression avec un polynôme de la forme de l’équation 8.1.1.2. Rappelons une fois de plus que selon la définition 3,8.1.1.3 DÉFINITION et expression du coefficient de détermination
 prise en compte par la courbe de régression. Il est possible de calculer l’équation 8.1.1.3 à la main, mais la manière la plus simple de déterminer
prise en compte par la courbe de régression. Il est possible de calculer l’équation 8.1.1.3 à la main, mais la manière la plus simple de déterminer 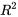 est bien entendu d’utiliser un outil de calcul statistique informatique.
est bien entendu d’utiliser un outil de calcul statistique informatique.Exemple 8.1.1.2 (suite)
Les captures d’écran ci-dessus montrent que l’équation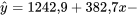
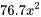 donne
donne 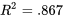 . Donc
. Donc 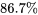 de la variabilité totale concernant la résistance à la compression est prise en compte par l’équation de régression quadratique. Le coefficient de corrélation entre les valeurs de résistance observées
de la variabilité totale concernant la résistance à la compression est prise en compte par l’équation de régression quadratique. Le coefficient de corrélation entre les valeurs de résistance observées 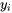 et les valeurs de résistance ajustées
et les valeurs de résistance ajustées 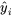 est
est 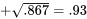 .
.
.
En comparant ce qui a été fait dans cette section à ce qui a été fait dans la partie 7.1, il est intéressant de noter que pour l’ajustement des données sur les cendres volantes par une droite, la valeur de 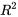 était de -0,005 (à trois décimales). La régression quadratique constitue une amélioration remarquable par rapport à la régression linéaire pour représenter ces données.
était de -0,005 (à trois décimales). La régression quadratique constitue une amélioration remarquable par rapport à la régression linéaire pour représenter ces données.
 ont été élevées au carré et au cube pour obtenir les valeurs de
ont été élevées au carré et au cube pour obtenir les valeurs de 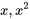 et
et 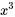 à utiliser pour la régression pour chaque valeur de
à utiliser pour la régression pour chaque valeur de  .
.
.

.
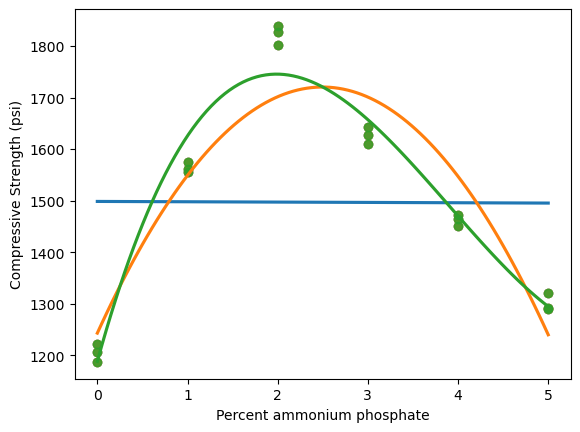
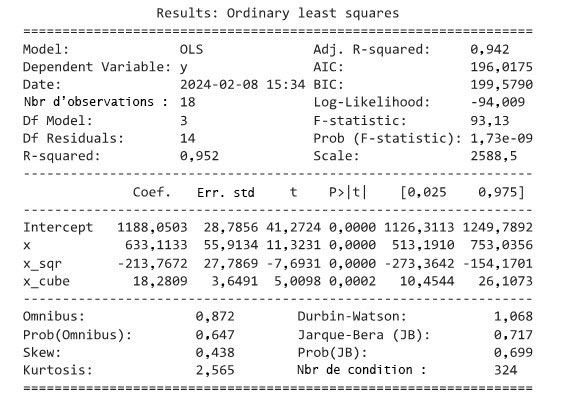
La valeur obtenue pour 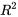 en utilisant une équation du troisième degré est de 0,952, soit un peu plus qu’en utilisant une équation du second degré. Mais la figure 8.1.1.2 montre clairement que même un polynôme du troisième degré ne permet pas d’obtenir une représentation totalement satisfaisante de ces données. Les courbes de régression quadratique et cubique présentées sur les figures 8.1.1.2 et 8.1.1.1 ne s’ajustent pas de manière satisfaisante avec les données de x =
en utilisant une équation du troisième degré est de 0,952, soit un peu plus qu’en utilisant une équation du second degré. Mais la figure 8.1.1.2 montre clairement que même un polynôme du troisième degré ne permet pas d’obtenir une représentation totalement satisfaisante de ces données. Les courbes de régression quadratique et cubique présentées sur les figures 8.1.1.2 et 8.1.1.1 ne s’ajustent pas de manière satisfaisante avec les données de x = 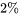 . Malheureusement, il s’agit de la zone où la résistance à la compression est la plus importante – exactement la zone présentant le plus grand intérêt d’un point de vue pratique.
. Malheureusement, il s’agit de la zone où la résistance à la compression est la plus importante – exactement la zone présentant le plus grand intérêt d’un point de vue pratique.
Cet exemple illustre le fait que 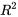 n’est pas le seul élément à prendre en compte pour évaluer la pertinence du polynôme d’un modèle de régression, et qu’il faut également examiner les graphiques. Les diagrammes en nuage de points de
n’est pas le seul élément à prendre en compte pour évaluer la pertinence du polynôme d’un modèle de régression, et qu’il faut également examiner les graphiques. Les diagrammes en nuage de points de  en fonction de
en fonction de  et les courbes de régression superposées peuvent être utiles, mais les graphiques des résidus aussi. Ceci peut être illustré avec un ensemble de données où la relation attendue entre
et les courbes de régression superposées peuvent être utiles, mais les graphiques des résidus aussi. Ceci peut être illustré avec un ensemble de données où la relation attendue entre  et
et  est presque parfaitement quadratique.
est presque parfaitement quadratique.
Exemple 8.1.1.3 Analyse des données lors du lâcher d’une masse
 ont été enregistrées à intervalles de
ont été enregistrées à intervalles de 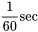 à partir d’un instant
à partir d’un instant 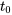 inconnu (inférieur à
inconnu (inférieur à 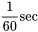 ) après que la masse soit lâche. Étant donné que la physique newtonienne prévoit que le déplacement de la masse vaut
) après que la masse soit lâche. Étant donné que la physique newtonienne prévoit que le déplacement de la masse vaut
8.1.1.4.
 est supposé avoir une relation approximativement quadratique avec
est supposé avoir une relation approximativement quadratique avec et, effectivement, le graphique des paires
et, effectivement, le graphique des paires 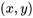 de la figure de la partie 1 semble présenter ce caractère.
de la figure de la partie 1 semble présenter ce caractère.8.1.1.5
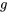 (en
(en 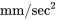 ) sera égale à
) sera égale à 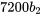 . C’est par cette méthode que la valeur
. C’est par cette méthode que la valeur 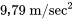 , présentée à la section 1.4 a été obtenue.
, présentée à la section 1.4 a été obtenue.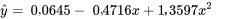
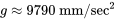 ) avec
) avec 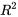 valant 1,0, à six décimales près. Dans le cas de cette régression, les résidus peuvent être déterminés en utilisant la définition 8.1.1.3. Ils sont présentés dans le tableau 8.1.1.1. La figure 8.1.1.3 présente un graphique normal des résidus. Il est raisonnablement linéaire et ne présente donc rien de remarquable (à l’exception d’une légère suggestion selon laquelle le ou les deux résidus les plus importants ne sont peut-être pas aussi extrêmes qu’on pourrait le prévoir, une situation qui ne présente pas d’explication physique apparente).
valant 1,0, à six décimales près. Dans le cas de cette régression, les résidus peuvent être déterminés en utilisant la définition 8.1.1.3. Ils sont présentés dans le tableau 8.1.1.1. La figure 8.1.1.3 présente un graphique normal des résidus. Il est raisonnablement linéaire et ne présente donc rien de remarquable (à l’exception d’une légère suggestion selon laquelle le ou les deux résidus les plus importants ne sont peut-être pas aussi extrêmes qu’on pourrait le prévoir, une situation qui ne présente pas d’explication physique apparente).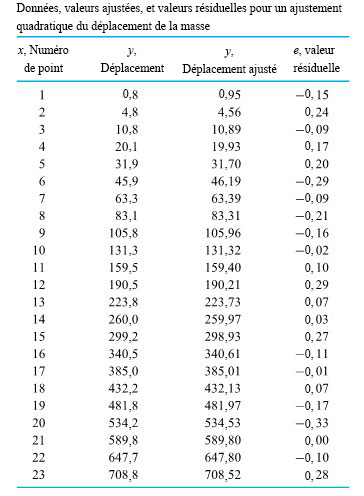
.
.
.
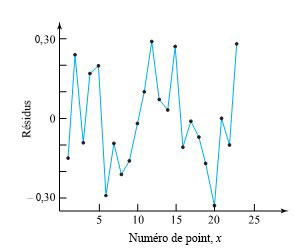
Toutefois, un graphique des résidus en fonction de  (observations chronologiques) est intéressant. Ce type de graphique est présenté sur la figure 8.1.1.4; les points successifs ont été reliés par des segments de droite. La figure 8.1.1.4 laisse supposer l’existence d’une tendance cyclique dans les résidus. Les valeurs des déplacements observées sont à tour de rôle trop élevées, puis trop basses, puis trop élevées, etc. Il serait intéressant de regarder d’autres rubans expérimentaux pour voir si ce modèle cyclique apparaît de manière constante avant de se pencher sérieusement sur son origine. Mais si la tendance suggérée par la figure 8.1.1.4 réapparaissait systématiquement, cela indiquerait que quelque chose dans le mécanisme qui génère un courant à 60 Hz peut entraîner des cycles alternativement un peu plus courts et un peu plus longs que
(observations chronologiques) est intéressant. Ce type de graphique est présenté sur la figure 8.1.1.4; les points successifs ont été reliés par des segments de droite. La figure 8.1.1.4 laisse supposer l’existence d’une tendance cyclique dans les résidus. Les valeurs des déplacements observées sont à tour de rôle trop élevées, puis trop basses, puis trop élevées, etc. Il serait intéressant de regarder d’autres rubans expérimentaux pour voir si ce modèle cyclique apparaît de manière constante avant de se pencher sérieusement sur son origine. Mais si la tendance suggérée par la figure 8.1.1.4 réapparaissait systématiquement, cela indiquerait que quelque chose dans le mécanisme qui génère un courant à 60 Hz peut entraîner des cycles alternativement un peu plus courts et un peu plus longs que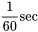 . Conséquence pratique de cette observation : si une mesure plus précise de altgalttitlegtitle était envisagée, il faudrait prendre en compte la régularité de la variation du courant
. Conséquence pratique de cette observation : si une mesure plus précise de altgalttitlegtitle était envisagée, il faudrait prendre en compte la régularité de la variation du courant 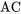 .
.
Que faire si un polynôme ne permet pas la régression de données 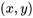 ?
?
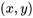 au moyen d’une équation polynomiale. Naturellement, des situations telles que celle de l’exemple 8.1.1.3 se présentent parfois, et il est raisonnable de s’interroger sur ce que l’on peut en tirer. Il convient de garder à l’esprit deux choses simples.
au moyen d’une équation polynomiale. Naturellement, des situations telles que celle de l’exemple 8.1.1.3 se présentent parfois, et il est raisonnable de s’interroger sur ce que l’on peut en tirer. Il convient de garder à l’esprit deux choses simples. et
et  en tous points, il peut tout à fait être pertinent de manière locale, c’est-à-dire pour une plage relativement restreinte des valeurs de
en tous points, il peut tout à fait être pertinent de manière locale, c’est-à-dire pour une plage relativement restreinte des valeurs de  . Par exemple dans l’étude des cendres volantes, la représentation quadratique de la résistance à la compression comme une fonction du pourcentage de phosphate d’ammonium n’est pas appropriée pour la plage 0 à
. Par exemple dans l’étude des cendres volantes, la représentation quadratique de la résistance à la compression comme une fonction du pourcentage de phosphate d’ammonium n’est pas appropriée pour la plage 0 à 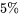 . Mais la région autour de
. Mais la région autour de 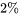 ayant été identifiée comme une zone d’intérêt particulier, il serait pertinent de mener une étude de suivi en se concentrant (par exemple) sur les données entre 1,5 % et 2,5 % de phosphate d’ammonium.
ayant été identifiée comme une zone d’intérêt particulier, il serait pertinent de mener une étude de suivi en se concentrant (par exemple) sur les données entre 1,5 % et 2,5 % de phosphate d’ammonium.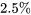 Il est tout à fait possible qu’une régression quadratique réalisée uniquement pour la plage de données
Il est tout à fait possible qu’une régression quadratique réalisée uniquement pour la plage de données 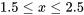 soit satisfaisante et utile pour une synthèse de l’étude de suivi.
soit satisfaisante et utile pour une synthèse de l’étude de suivi.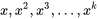 de l’équation 8.1.1.2 peuvent être remplacés par n’importe quelle fonction (connue) de
de l’équation 8.1.1.2 peuvent être remplacés par n’importe quelle fonction (connue) de  et ce que nous avons dit ici restera inchangé pour l’essentiel. Cela nous amène à considérer la transformation de termes pour parvenir à une régression plus satisfaisante.
et ce que nous avons dit ici restera inchangé pour l’essentiel. Cela nous amène à considérer la transformation de termes pour parvenir à une régression plus satisfaisante.