7.2.4 Intervalles de prédiction et de tolérance
L’inférence pour 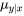 est une réponse à la question qualitative : « Si on garde
est une réponse à la question qualitative : « Si on garde
la variable d’entrée x constante, à quelles réponses peut-on s’attendre de la part du système? » Il s’agit d’une réponse exprimée sous forme de moyenne ou de moyenne à long terme, mais parfois, il est plus pratique d’avoir une réponse exprimée sous forme de réponses individuelles. Dans ces cas, il est utile de savoir que les hypothèses du modèle de régression linéaire simple 7.2.1.2 donnent leurs propres équations spécifiques pour les intervalles de prédiction et de tolérance.
Le fait de base qui rend possible les intervalles de prédiction dans les hypothèses de l’équation 7.2.1.2 est que si 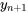 est une observation supplémentaire, provenant de la distribution des réponses correspondant à un x donné, et que
est une observation supplémentaire, provenant de la distribution des réponses correspondant à un x donné, et que 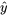 est la valeur ajustée correspondante à ce x (selon les n paires de données d’origine), alors
est la valeur ajustée correspondante à ce x (selon les n paires de données d’origine), alors
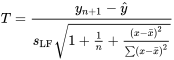
suit une distribution 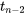 . Habituellement, ce fait conduit à la conclusion que, dans le cadre du
. Habituellement, ce fait conduit à la conclusion que, dans le cadre du
modèle 7.2.1.2, l’intervalle bilatéral dont les bornes sont
7.2.4.1 Limites de prédiction de la régression linéaire simple pour un y supplémentaire à un x donné
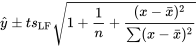
peut être utilisé comme intervalle de prédiction pour une observation supplémentaire y à une valeur donnée de la variable d’entrée x. La confiance de prédiction associée est la probabilité que la distribution 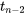 attribue à l’intervalle entre -t et t. Les intervalles unilatéraux s’obtiennent de la manière habituelle, en utilisant une seule borne dans l’équation 7.2.4.1 et en ajustant le niveau de confiance en conséquence.
attribue à l’intervalle entre -t et t. Les intervalles unilatéraux s’obtiennent de la manière habituelle, en utilisant une seule borne dans l’équation 7.2.4.1 et en ajustant le niveau de confiance en conséquence.
Il est possible non seulement de dériver des formules d’intervalles de prédiction à partir des hypothèses du modèle de régression linéaire simple, mais aussi de définir des formules relativement simples pour les limites de tolérance unilatérales approximatives. Autrement dit, les intervalles
7.2.4.2 Intervalle de tolérance unilatéral pour la distribution y à x
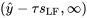
et
7.2.4.3 Autre intervalle de tolérance unilatéral pour la distribution y à x
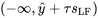
peuvent être utilisés comme intervalles de tolérance unilatéraux pour une fraction p de la distribution sous-jacente des réponses correspondant à une valeur donnée de la variable du système x, à condition que le paramètre 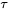 soit choisi de manière appropriée (en fonction des données, de p, de x et du niveau de confiance souhaité).
soit choisi de manière appropriée (en fonction des données, de p, de x et du niveau de confiance souhaité).
7.2.4.4 Rapport de 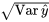 sur
sur 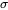 pour la régression linéaire simple
pour la régression linéaire simple
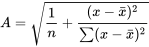
sera adopté comme multiplicateur (p. ex., dans l’équation précédente pour passer d’une estimation de σ à une estimation de l’écart-type de 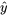 ). Puis, pour situer une fraction p des réponses au point x avec un niveau de confiance d’approximativement
). Puis, pour situer une fraction p des réponses au point x avec un niveau de confiance d’approximativement 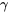 , le
, le 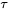 approprié dans l’intervalle de l’équation 7.2.4.2 ou 7.2.4.3 est le suivant :
approprié dans l’intervalle de l’équation 7.2.4.2 ou 7.2.4.3 est le suivant :
7.2.4.5 Multiplicateur à utiliser dans les limites de tolérance
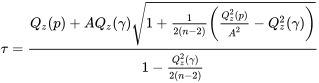
Exemple 7.2.4.1 (suite)
Pour illustrer l’utilisation des équations d’intervalles de prédiction et de tolérance dans le contexte d’une régression linéaire simple, prenons l’exemple d’une limite inférieure de prédiction de 90 % pour une donnée de densité supplémentaire avec une pression de 4 000 psi. Puis, trouvons une limite de tolérance inférieure de 95 % pour 90 % des nombreuses densités de cylindre supplémentaires à cette même pression.
En commençant par le problème de prédiction, l’équation 7.2.4.1 montre qu’une limite de prédiction appropriée est la suivante :
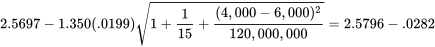
soit
2,5514 g/cc
Si, au lieu de prévoir une seule densité supplémentaire pour x = 4 000 psi, il faut trouver 90 % des densités supplémentaires correspondant à une pression de 4 000 psi, il convient d’établir une limite de tolérance. Utilisons d’abord l’équation 7.2.4.4 :
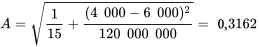
Ensuite, pour une confiance de 95 %, l’équation 7.4.4.5 donne :
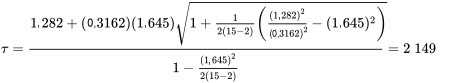
Enfin, la limite inférieure de tolérance d’environ 95 % pour 90 % des densités produites avec une pression de 4 000 psi vaut (selon l’équation 7.2.4.2) :
2,5697-2,149(0,0199)=2,5697-0,0428
soit
2,5269 g/cc
Mises en garde concernant les intervalles de prédiction et de tolérance dans la régression
Étant donné que l’ajustement des courbes facilite l’interpolation et l’extrapolation, il est essentiel de faire preuve de prudence dans l’interprétation des intervalles de prédiction et de tolérance. Toutes les mises en garde concernant l’interprétation des intervalles de prédiction et de tolérance soulevées dans la partie 5 s’appliquent également à la présente situation. Ici, il faut être encore plus prudent en raison du fait que les intervalles peuvent être calculés pour des valeurs de x pour lesquelles on ne dispose d’aucune donnée. Si on veut utiliser les équations 7.2.4.1, 7.2.4.2 et 7.2.4.3 pour une valeur de x autre que 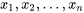 , il doit être plausible que le modèle 7.2.1.2 décrive le comportement du système non seulement pour les valeurs de x pour lesquelles on dispose de données, mais aussi pour la nouvelle valeur de x. Et même lorsque ce modèle est « plausible », l’application des équations 7.2.4.1, 7.2.4.2 et 7.2.4.3 à de nouvelles valeurs de x doit être traitée avec prudence. Si ce jugement (non vérifié) s’avère erroné, le niveau de confiance nominal n’a aucune pertinence pratique.
, il doit être plausible que le modèle 7.2.1.2 décrive le comportement du système non seulement pour les valeurs de x pour lesquelles on dispose de données, mais aussi pour la nouvelle valeur de x. Et même lorsque ce modèle est « plausible », l’application des équations 7.2.4.1, 7.2.4.2 et 7.2.4.3 à de nouvelles valeurs de x doit être traitée avec prudence. Si ce jugement (non vérifié) s’avère erroné, le niveau de confiance nominal n’a aucune pertinence pratique.
