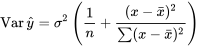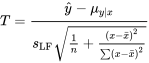7.2.3 Inférence pour la moyenne de la réponse d’un système pour une valeur particulière de x
Au chapitre 6, nous avons abordé le problème de l’estimation de la moyenne de y avec les niveaux du ou des facteurs considérés. À présent, le problème analogue est celui de l’estimation de la réponse moyenne pour une valeur fixée de la variable du système x,
7.2.3.1
L’approximation naturelle (et basée sur des données) de la moyenne dans l’équation 7.2.3.1 est la valeur y correspondante tirée de la droite des moindres carrés. La notation
7.2.3.2 Estimateur de 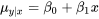
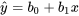
sera utilisée pour cette valeur sur les droites des moindres carrés. (Et ce, malgré le fait que la valeur de l’équation 7.2.3.2 peut ne pas être une valeur ajustée au sens où cette expression a été le plus souvent utilisée jusqu’à présent. Il n’est pas nécessaire que  soit égal à
soit égal à  pour que les expressions 7.2.3.1 et 7.2.3.2 soient valables.) Le modèle de régression linéaire simple (équation 7.2.1.2) donne des propriétés de distribution simples pour
pour que les expressions 7.2.3.1 et 7.2.3.2 soient valables.) Le modèle de régression linéaire simple (équation 7.2.1.2) donne des propriétés de distribution simples pour  , qui mènent à des méthodes d’inférence pour
, qui mènent à des méthodes d’inférence pour  .
.
Selon le modèle 7.2.1.2, 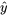 suit une distribution normale avec
suit une distribution normale avec
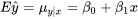
et
7.2.3.3
(Dans l’expression 7.2.3.3, on a un peu abusé de la notation. Les indices  de la somme dans
de la somme dans 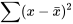 ont été supprimés. Cette sommation porte sur les
ont été supprimés. Cette sommation porte sur les 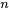 valeurs
valeurs 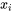 de l’ensemble de données original. D’autre part, dans le terme
de l’ensemble de données original. D’autre part, dans le terme 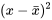 du numérateur de l’expression 7.2.3.3, le
du numérateur de l’expression 7.2.3.3, le  considéré n’est pas nécessairement égal à l’un des
considéré n’est pas nécessairement égal à l’un des 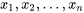 . Il s’agit plutôt de la valeur de la variable du système à laquelle la réponse moyenne doit être estimée.) Ainsi,
. Il s’agit plutôt de la valeur de la variable du système à laquelle la réponse moyenne doit être estimée.) Ainsi,
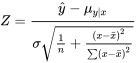
suit une distribution normale standard, ce qui implique que
7.2.3.4
suit une distribution 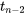 . Les arguments standard de la partie 5 appliqués à l’expression 7.2.3.4 montrent alors que
. Les arguments standard de la partie 5 appliqués à l’expression 7.2.3.4 montrent alors que
7.2.3.5
peut être testée à l’aide de la statistique de test (aussi appelée variable de décision)
7.2.3.6 Statistique de test pour 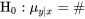
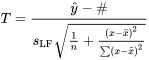
et d’une distribution de référence 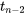 . De plus, dans le cadre du modèle de régression linéaire simple
. De plus, dans le cadre du modèle de régression linéaire simple
(équation 7.2.1.2), un intervalle de confidence individuel bilatéral pour 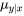 peut être établi avec les bornes suivantes :
peut être établi avec les bornes suivantes :
7.2.3.7 Limites de confiance pour la réponse moyenne, 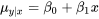
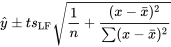
où le niveau de confiance associé correspond à la probabilité assignée à l’intervalle entre 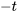 et
et  dans la distribution
dans la distribution 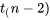 . Un intervalle de confiance unilatéral s’obtient de la manière habituelle, en utilisant une seule borne dans l’équation 7.2.3.7.
. Un intervalle de confiance unilatéral s’obtient de la manière habituelle, en utilisant une seule borne dans l’équation 7.2.3.7.
Exemple 7.2.3.1 (suite)
Revenons à l’étude de la pression et de la densité. Établissons des intervalles de confidence individuels à 95 % pour les densités moyennes des cylindres obtenus d’abord à 4 000 psi, puis à 5 000 psi.
En commençant avec x = 4 000 psi, l’estimation correspondante de la densité moyenne est la suivante :

De plus, d’après l’équation 7.2.3.7 et le fait que le quantile 0,975 de la distribution 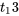 vaut 2,160, une précision de plus ou moins
vaut 2,160, une précision de plus ou moins

peut être associée à la valeur de 2,5697 g/cc. Autrement dit, les bornes d’un intervalle de confidence bilatéral à 95 % pour la densité moyenne dans la condition de 4 000 psi sont les suivantes :
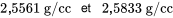
À x = 5 000 psi, l’estimation correspondante de la densité moyenne est la suivante :
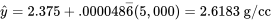
D’après l’équation 7.2.3.7, une précision de plus ou moins
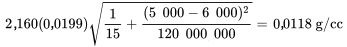
peut être associée à la valeur de 2,6183 g/cc. Autrement dit, les bornes d’un intervalle de confidence bilatéral à 95 % pour la densité moyenne dans la condition de 5 000 psi sont les suivantes :
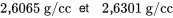
Il convient de comparer les valeurs plus ou moins des deux intervalles de confidence trouvés. L’intervalle pour x = 5 000 psi est plus court et donc plus parlant que l’intervalle pour x = 4 000 psi. L’origine de cette divergence devrait être claire, du moins après examen de l’équation 7.2.3.7. Selon les données de l’étude,
 = 6 000 psi.
= 6 000 psi.  = 5 000 psi est plus proche de
= 5 000 psi est plus proche de  que x = 4 000 psi. Ainsi,
que x = 4 000 psi. Ainsi, 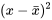 (et donc la longueur de l’intervalle) est plus petit pour x = 5 000 psi que pour x = 4 000 psi.
(et donc la longueur de l’intervalle) est plus petit pour x = 5 000 psi que pour x = 4 000 psi.
Le phénomène observé dans l’exemple précédent, à savoir que la longueur d’un intervalle de confidence pour 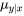 augmente à mesure que l’on s’éloigne de
augmente à mesure que l’on s’éloigne de 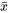 , est important. De plus, il a une signification intuitivement plausible pour la planification d’expériences lors desquelles on s’attend à une relation approximativement linéaire entre y et x, où x est une variable contrôlée. S’il y a un intervalle de valeurs de x sur lequel on veut obtenir une bonne précision dans l’estimation des réponses moyennes, il est logique de centrer les efforts de collecte de données sur cet intervalle.
, est important. De plus, il a une signification intuitivement plausible pour la planification d’expériences lors desquelles on s’attend à une relation approximativement linéaire entre y et x, où x est une variable contrôlée. S’il y a un intervalle de valeurs de x sur lequel on veut obtenir une bonne précision dans l’estimation des réponses moyennes, il est logique de centrer les efforts de collecte de données sur cet intervalle.
Inférence pour l’ordonnée à l’origine 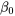
Une bonne utilisation des équations 7.2.3.5, 7.2.3.6 et 7.2.3.7 donne des méthodes d’inférence pour le paramètre 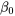 du modèle 7.2.1.2, l’ordonnée à l’origine de la relation linéaire (équation 7.2.3.1).
du modèle 7.2.1.2, l’ordonnée à l’origine de la relation linéaire (équation 7.2.3.1).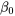 Ainsi, en fixant x = 0 dans les équations 7.2.3.5, 7.2.3.6 et 7.2.3.7, on obtient des tests et des intervalles de confidence
Ainsi, en fixant x = 0 dans les équations 7.2.3.5, 7.2.3.6 et 7.2.3.7, on obtient des tests et des intervalles de confidence
pour 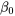 . Cependant, à moins que x = 0 soit une valeur réalisable pour la variable d’entrée
. Cependant, à moins que x = 0 soit une valeur réalisable pour la variable d’entrée
et que la région où la relation linéaire (équation 7.2.3.1) est une description raisonnable de la réalité physique comprenne x = 0, l’inférence pour 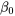 seul est rarement d’un intérêt pratique.
seul est rarement d’un intérêt pratique.
Limites de confiance bilatérales simultanées pour toutes les moyennes 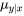
7.2.3.8 Intervalle de confiance à 95 % de la réponse moyenne
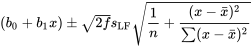
où, la confiance simultanée associée est la probabilité 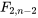 attribuée à l’intervalle [0,
attribuée à l’intervalle [0, 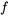 ] (avec
] (avec 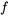 positif).
positif).
Bien entendu, par « toutes les moyennes 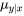 », on veut en vérité dire « pour toutes les réponses moyennes dans un intervalle où le modèle de régression linéaire simple 7.2.1.2 est une description adéquate de la relation entre x et y ». Comme c’est toujours le cas pour l’ajustement des courbes et des surfaces, il est risqué d’extrapoler en dehors de la plage de valeurs de x pour laquelle on dispose de données (et même, dans une certaine mesure, d’interpoler dans cette plage). Toute extrapolation doit être étayée par une expertise dans le domaine, afin de prouver qu’elle est justifiable.
», on veut en vérité dire « pour toutes les réponses moyennes dans un intervalle où le modèle de régression linéaire simple 7.2.1.2 est une description adéquate de la relation entre x et y ». Comme c’est toujours le cas pour l’ajustement des courbes et des surfaces, il est risqué d’extrapoler en dehors de la plage de valeurs de x pour laquelle on dispose de données (et même, dans une certaine mesure, d’interpoler dans cette plage). Toute extrapolation doit être étayée par une expertise dans le domaine, afin de prouver qu’elle est justifiable.
Il peut être quelque peu difficile de saisir la signification d’une valeur de confiance simultanée applicable à tous les intervalles possibles de la forme 7.2.3.8. Jusqu’à présent, les niveaux de confiance étudiés l’ont été pour des ensembles finis d’intervalles. La meilleure façon de comprendre l’ensemble théoriquement infini d’intervalles donné par l’équation 7.2.3.8 est probablement de définir une région du plan (x, y) qu’on suppose contenir la droite 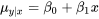 . La figure 7.2.3.1 représente une région de confiance typique obtenue par l’équation 7.2.3.8. Il y a une région indiquée autour de la droite des moindres carrés dont l’étendue verticale augmente avec la distance par rapport à
. La figure 7.2.3.1 représente une région de confiance typique obtenue par l’équation 7.2.3.8. Il y a une région indiquée autour de la droite des moindres carrés dont l’étendue verticale augmente avec la distance par rapport à 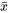 et qui couvre, pour le niveau de confiance donné, la droite décrivant la relation entre
et qui couvre, pour le niveau de confiance donné, la droite décrivant la relation entre  et
et 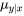 .
.
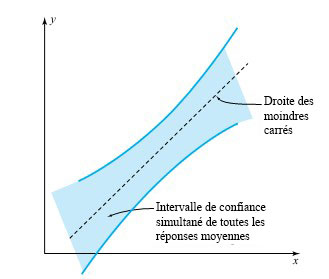
par des intervalles de confiance simultanés pour toutes les valeurs de [latex]\mu_{y \mid x}[/latex].
Exemple 7.2.3.2 (suite)
Au moyen de l’équation 7.2.3.8, on peut trouver les intervalles de confiance simultanés à 95 % pour la densité moyenne des cylindres obtenus dans les cinq conditions d’expérimentation réelles.
Puisque il faut utiliser l’équation 7.2.3.8 avec 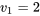 et
et 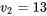 degrés de liberté, il convient d’utiliser des limites simultanées de la forme
degrés de liberté, il convient d’utiliser des limites simultanées de la forme

Cela peut également se comparer à l’utilisation de la méthode P-R de la partie 6 pour le calcul simultané de l’intervalle de confiance à 95 %.
Tout d’abord, la formule (de la partie 6) montre qu’avec n − r = 15 − 5 = 10 degrés de liberté pour 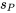 et r = 5 conditions étudiées, les limites de confiance bilatérales simultanées à 95 % pour les cinq densités moyennes sont de la forme suivante :
et r = 5 conditions étudiées, les limites de confiance bilatérales simultanées à 95 % pour les cinq densités moyennes sont de la forme suivante :
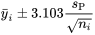
En l’occurrence,
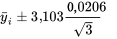
soit
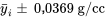
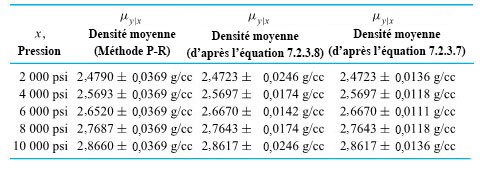
Le tableau 7.2.3.1 présente les cinq intervalles résultant de l’utilisation de deux méthodes d’intervalles de confiance simultanées, ainsi que les intervalles individuels de l’équation 7.2.3.7.
Deux faits ressortent de ce tableau. Premièrement, les intervalles résultant de l’équation 7.2.3.8 sont un peu plus larges que les intervalles individuels correspondants donnés par l’équation 7.2.3.7. Deuxièmement, il est également clair que l’utilisation des hypothèses du modèle de régression linéaire simple plutôt que les hypothèses à un facteur plus générales de la partie 6 peut conduire à des intervalles de confidence simultanés plus courts et à des déductions techniques réelles plus nettes.