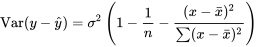7.2.1 Modèle de régression linéaire simple, estimation de la variance correspondante et résidus normalisés

C. Bassim et Bryan Lee

7.2.1 Modèle de régression linéaire simple, estimation de la variance correspondante et résidus normalisés

À la partie 6, nous avons vu que le modèle à un facteur (même variance, distribution normale) est la base de probabilité la plus courante des méthodes d’inférence pour les études multi-échantillons. Il était représenté par les symboles

7.2.1.1 $y_{i j}=\mu_i+\epsilon_{i j}$

où les moyennes 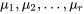$\mu_1, \mu_2, \ldots, \mu_r$ étaient considérées comme r paramètres non limités. Dans le cas d’une inférence basée sur les paires de données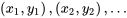 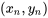$\left(x_1, y_1\right),\left(x_2, y_2\right), \ldots$ $\left(x_n, y_n\right)$ dont le nuage de points est approximativement linéaire, il faut à nouveau imposer une restriction au modèle à un facteur 7.2.1.1. En mots, les hypothèses du modèle seront qu’il y a des distributions normales sous-jacentes pour la réponse y avec une variance commune 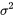$\sigma^2$ , mais que les moyennes 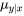$\mu_{y \mid x}$ varient de façon linéaire en fonction de $x$ . En symboles, il est courant d’écrire que pour $i = 1, 2,...,n$ :

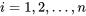Modèle de régression
linéaire simple
(normal) 7.2.1.2

$y_i=\beta_0+\beta_1 x_i+\epsilon_i$

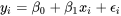
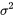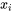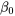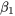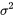où les i sont des variables aléatoires (non observables) indépendantes et identiquement distribuées (iid) suivant une distribution normale (0, $\sigma^2$ ), les $x_i$ sont des constantes connues, et $\beta_0$ , $\beta_1$ et $\sigma^2$ sont des paramètres inconnus du modèle (constantes fixes). Le modèle 7.2.1.2 est couramment appelé modèle de régression linéaire simple (normal).

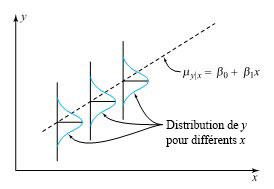
Si on considère que les différentes valeurs de x dans un ensemble de données (x, y) le « séparent » en divers échantillons de y, l’expression 7.2.1.2 est la formulation du modèle 7.2.1.1 dans lequel les moyennes (auparavant non limitées) satisfont à la relation linéaire 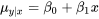$\mu_{y \mid x}=\beta_0+\beta_1 x$ . La figure 7.2.1.1 est une représentation graphique du modèle « distribution normale, variance constante, moyenne linéaire (en x) ».

Figure 7.2.1.1 Représentation graphique du modèle de régression linéaire simple

Les inférences sur les quantités comprenant les valeurs x représentées dans les données (comme la réponse moyenne à un x donné ou la différence entre les réponses moyennes à deux valeurs différentes de x) seront généralement plus précises lorsqu’on peut utiliser des méthodes basées sur le modèle 7.2.1.2 plutôt que les méthodes générales de la partie 6 et d’ANOVA. Et dans la mesure où le modèle 7.2.1.2 décrit le comportement du système pour des valeurs de x non incluses dans les données, un tel modèle permet de faire des inférences limitées d’interpolation et d’extrapolation limitées sur x.

Le module 7.1 aborde en détail l’utilisation des moindres carrés dans l’ajustement de la relation approximativement linéaire

7.2.1.3 $y \approx \beta_0+\beta_1 x$

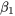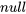
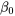à un ensemble de données (x, y). À présent, nous pouvons constater que le module 7.1 peut être considéré comme une présentation de la régression et de l’utilisation des résidus dans la vérification du modèle pour la régression linéaire simple (équation 7.2.1.2). Plus particulièrement, les estimations de $\beta_1$ et de $\text{[math]}$ $\beta_0$ sont associées au modèle de régression linéaire simple, que nous montrons à nouveau ici :

Pente de la droite des moindres carrés 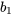$b_1$ 7.2.1.3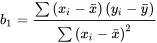 $b_1=\frac{\sum\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sum\left(x_i-\bar{x}\right)^2}$

et

Ordonnée à l’origine de la droite des moindres carrés 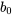$b_0$ 7.2.1.4

$b_0=\bar{y}-b_1 \bar{x}$

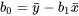
ainsi que les valeurs ajustées correspondantes

Valeurs ajustées pour la régression linéaire simple 7.2.1.5

$\hat{y}_i=b_0+b_1 x_i$

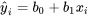
et les résidus

Résidus pour la régression linéaire simple 7.2.1.6

$e_i=y_i-\hat{y}_i$

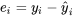
De plus, les résidus (ou erreurs) de l’équation 7.2.1.6 peuvent servir à estimer 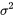$\sigma^2$ . Comme toujours, la somme des résidus au carré est divisée par un nombre approprié de degrés de liberté. La définition ci-dessous est celle d’une régression linéaire simple ou d’une variance d’échantillon d’une régression de droite, que nous appellerons l’erreur quadratique moyenne de la régression de droite ( 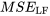$MSE_{\mathrm{LF}}$ , de l’anglais mean squared error et line fitting).

Erreur quadratique moyenne du modèle de régression linéaire simple d’une droite

DÉFINITION Erreur quadratique moyenne du modèle de régression linéaire simple d’une droite (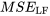 $MSE_{\mathrm{LF}}$ )

EXPRESSION 7.2.1.7

$MSE_{\mathrm{LF}} = s_{\mathrm{LF}}^2=\frac{1 }{n-2} \sum(y-\hat{y})^2=\frac{1 }{n-2} \sum e^2$

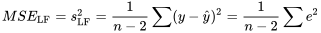
est l’erreur quadratique moyenne de la régression d’une droite (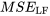 $MSE_{\mathrm{LF}}$ ). Il s’agit de l’ajustement (par régression linéaire simple) de la variance de l’erreur de l’échantillon ( $s_{\mathrm{LF}}^2$ ).

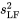Elle est associée aux 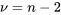$\nu=n-2$ degrés de liberté et à l’erreur type du modèle de régression d’une droite ( 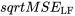$\sqrt{MSE_{\mathrm{LF}}}$ , une estimation de l’écart-type de la variable de réponse ( $\sqrt{s_{\mathrm{LF}}^2}$ ).

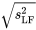DÉFINITION Erreur type du modèle de régression linéaire simple d’une droite (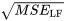 $\sqrt{MSE_{\mathrm{LF}}}$ )

EXPRESSION 7.2.1.8

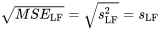
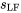$\sqrt{MSE_{\mathrm{LF}}} =\sqrt{s_{\mathrm{LF}}^2} = s_{\mathrm{LF}}$

$s_{\mathrm{LF}}$ est une estimation de la variation de base 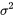$\sigma^2$ si le modèle de régression linéaire simple 7.2.1.2 décrit bien le système étudié.

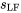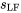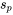Si ce n’est pas le cas, $s_{\mathrm{LF}}$ aura tendance à surestimer σ. La comparaison de $s_{\mathrm{LF}}$ à $s_p$ (l’écart-type de l’échantillon groupé) est donc une autre façon de déterminer si le modèle 7.2.1.2 est approprié. Un 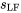$s_{\mathrm{LF}}$ beaucoup plus élevé que 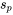$s_p$ laisse penser que le modèle de régression linéaire ne convient pas.

Example 7.2.1.1 Inférence dans l’étude sur le pressage de la poudre céramique (suite du module 7.1)

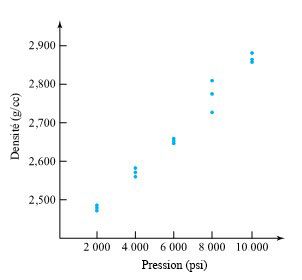
L’exemple principal de cette section sera l’étude de Benson, Locher et Watkins sur la pression et la densité, qui a été abondamment utilisée dans le module 7.1 pour illustrer l’analyse descriptive des données (x, y). Le tableau 7.2.1.1 présente à nouveau les n = 15 paires de données (x, y) (présentées pour la première fois dans le tableau 7.1.1.1), où

x = la pression utilisée (psi)
y = la densité obtenue (g/cc)

pour le pressage à sec d’un composé céramique en cylindres. La figure 7.2.1.1 est un nuage de points des données.

Rappelons également que d’après le calcul de 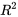$R^2$ , les données du tableau 7.2.1.1 donnent les valeurs ajustées du tableau 7.1.1.2, et que

$\sum(y-\hat{y})^2=0,005153$

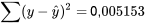
Ainsi, pour les données de pression et de densité, on obtient (par l’équation 7.2.1.7) que

$s_{\mathrm{LF}}^2=\frac{15-2}(0,005153)=0,000396(\mathrm{~g} / \mathrm{cc})^2$

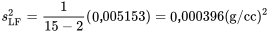
donc

$s_{\mathrm{LF}}=\sqrt{0,000396}=0,0199 \mathrm{~g} / \mathrm{cc}$

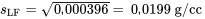
Si l’on accepte la pertinence du modèle 7.2.1.2 dans cet exemple, pour toute pression ﬁxe, l’écart-type des densités associées à de nombreux cylindres fabriqués à cette pression serait d’environ 0,02 g/cc.

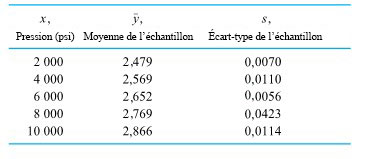
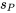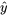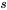Les données initiales de cet exemple peuvent être considérées comme organisées en r = 5 échantillons distincts de taille m = 3, un pour chacune des pressions de 2 000 psi, 4 000 psi, 6 000 psi, 8 000 psi et 10 000 psi. Ce raisonnement mène à une autre estimation de σ, soit $s_P$ . Le tableau 7.2.1.2 donne les valeurs de $\hat{y}$ et de $s$ pour les cinq échantillons.

Les écart-types des échantillons du tableau 7.2.1.2 peuvent être utilisés de la manière habituelle pour calculer 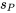$s_P$ . Donc (à partir de l’expression de la partie 5),

$s_{\mathrm{P}}^2=\frac{(3-1)(0,0070)^2+(3-1)(0,0110)^2+\cdots+(3-1)(0,0114)^2}{(3-1)+(3-1)+\cdots+(3-1)}$

$=0,000424(\mathrm{~g} / \mathrm{cc})^2$

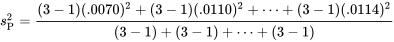
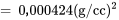
d’où

$s_{\mathrm{P}}=\sqrt{s_{\mathrm{P}}^2}=0,0206 \mathrm{~g} / \mathrm{cc}$

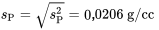
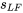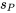Lorsqu’on compare $s_{LF}$ et $s_P$ , rien n’indique que ces valeurs soient mal ajustées.

Tableau 7.2.1.1 : Pressions de pressage et densité
de l’échantillon résultant

Figure 7.2.1.2. Nuage de points de la densité en fonction de la pression de pressage

Tableau 7.2.1.2 Moyenne et écart-type d’échantillon pour la densité obtenue avec cinq pressions de pressage différentes

Le module 7.1 comprend un tracé des résidus (équation 7.2.1.6) pour les données de pression et de densité (et notamment, un tracé normal à la figure 7.1.3.4). Même si les résidus (bruts) de l’équation 7.2.1.6 sont les plus faciles à calculer, la plupart des programmes de régression sur le marché proposent également de calculer les résidus normalisés. C’est même l’option privilégie par certains logiciels.

Résidus normalisés

Dans les analyses d’ajustement de courbes et de surfaces, la variance des résidus dépend de x.
La normalisation avant le tracé est un moyen d’éviter de confondre une tendance sur un tracé de résidus qui peut être expliquée par ces différentes variances avec une tendance qui indique des problèmes avec le modèle de base. Selon le modèle 7.2.1.2, pour un x donné avec la réponse correspondante y,

7.2.1.7 $\operatorname{Var}(y-\hat{y})=\sigma^2\left(1-\frac{1 }{n}-\frac{(x-\bar{x})^2}{\sum(x-\bar{x})^2}\right)$

Ainsi, à la lumière de l’équation 7.2.1.7 et des discussions sur la normalisation, la paire de données 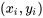$\left(x_i, y_i\right)$ est le résidu normalisé pour la régression linéaire simple.

Résidus normalisés pour la régression linéaire simple 7.2.1.8

$e_i^*=\frac{e_i}{s_{\mathrm{LF}} \sqrt{1-\frac{1 }{n}-\frac{\left(x_i-\bar{x}\right)^2}{\sum(x-\bar{x})^2}}}$

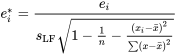
La méthode plus avancée pour examiner les résidus du modèle 7.2.1.2 consiste donc à tracer les valeurs de l’équation 7.2.1.8 plutôt que les résidus bruts (de l’équation 7.2.1.6).

Exemple 7.2.1.2 (suite)

Examinons comment les résidus normalisés pour l’ensemble de données de pression et de densité sont liés aux résidus bruts. En sachant que

\sum(x-\bar{x})^2=120 000 000

et que les valeurs 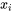$x_i$ des données initiales ne comprenaient que les pressions de 2 000 psi, 4 000 psi, 6 000 psi, 8 000 psi et 10 000 psi, il est facile d’obtenir les valeurs nécessaires de la racine dans le dénominateur de l’expression 7.2.1.8. Ces valeurs se trouvent dans le tableau 7.2.1.3.

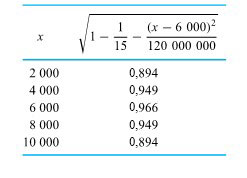
Tableau 7.2.1.3 Calculs des résidus normalisés dans l’étude de la pression et de la densité

Les données du tableau 7.2.1.3 montrent, par exemple, qu’il faut s’attendre à ce que les résidus correspondant à x = 6 000 psi soient (en moyenne) environ 0,966/0,894 = 1,08 fois plus importants que les résidus correspondant à x = 10 000 psi. Il faut diviser les résidus bruts par 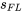$s_{FL}$ multiplié par la valeur correspondante de la deuxième colonne du tableau 7.2.1.3 pour les mettre sur un pied d’égalité. Le tableau 7.2.1.4 donne les résidus bruts
(tirés du module 7.1) et leurs contreparties normalisées.

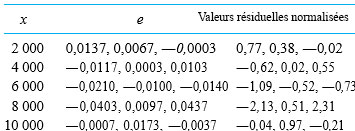
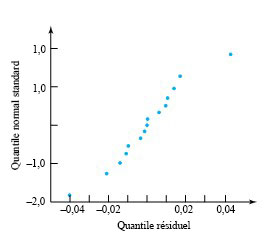
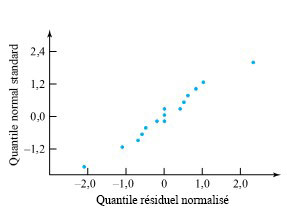
Tableau 7.2.1.4 Résidus bruts et normalisés de l’étude de la pression et de la densité

Dans le cas présent, étant donné que les valeurs 0,894, 0,949 et 0,966 sont assez comparables, la normalisation au moyen de l’équation 7.2.1.8 ne modifie pas beaucoup les conclusions relatives à la justesse du modèle. Par exemple, les figures 7.2.1.3 et 7.2.1.4 sont des tracés normaux des résidus bruts et des résidus normalisés (respectivement). À toutes fins pratiques, ils sont identiques. Par conséquent, toutes les conclusions (comme celles formulées dans le module 7.1) sur la justesse du modèle étayées par la figure 7.2.1.3 sont également étayées par la figure 7.2.1.4, et vice-versa.

Cependant, dans d’autres situations(en particulier lorsqu’un ensemble de données contient quelques valeurs de x très extrêmes), la normalisation peut comporter des dénominateurs plus variés pour l’équation 7.2.1.8 que ceux du tableau 7.2.1.3, ce qui aurait une incidence sur les résultats d’une analyse des résidus.

Figure 7.2.1.3 Tracé normal des résidus d’un ajustement linéaire aux données de pression et de la densité.

Figure 7.2.1.4 Tracé normal des résidus normalisés d’un ajustement linéaire aux données de pression et de la densité.

7.2.1 Modèle de régression linéaire simple, estimation de la variance correspondante et résidus normalisés

Licence

Partagez ce livre