7.2.0 Introduction aux méthodes d’inférence de la régression linéaire simple liées à la régression d’une droite selon la méthode des moindres carrés (régression linéaire simple)
Nous avons commencé l’étude des méthodes d’inférence pour les études multi-échantillons en abordant d’abord les méthodes qui n’utilisent pas explicitement la structure relative à plusieurs échantillons, et nous terminerons le cours en discutant de celles qui sont orientées vers l’analyse de la structure factorielle. Dans ce module, nous examinerons principalement les méthodes d’inférence pour les études à multi-échantillons lorsque les facteurs en cause sont intrinsèquement quantitatifs et qu’il est raisonnable de penser qu’il existe une relation fonctionnelle approximative entre les valeurs des variables du système, d’entrée ou indépendantes et les réponses observées du système. Autrement dit, ce chapitre présente et applique des méthodes d’inférence aux cas de régression des droites abordés dans le module 7.1.
Nous commencerons par examiner la situation la plus simple, à savoir celle où une variable de réponse y est liée de façon approximativement linéaire à une seule variable d’entrée quantitative x. Dans un tel contexte, on peut donner des formules explicites et illustrer en termes concrets les possibilités offertes par les méthodes d’inférence pour les analyses de régression. Nous aborderons l’analyse de régression multiple (régression de courbe et de surface) dans le prochain module.
Nous commencerons par examiner la situation la plus simple, à savoir celle où une variable de réponse y est liée de façon approximativement linéaire à une seule variable d’entrée quantitative x. Nous présentons tout d’abord le modèle de régression linéaire simple (normal) et expliquons comment estimer la variance de la réponse dans ce contexte. Ensuite, nous examinons les résidus normalisés. Puis, nous abordons le taux de variation 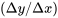 , ainsi que l’inférence pour la réponse moyenne à une valeur x donnée. Nous discuterons ensuite des intervalles de prévision et de tolérance pour les réponses à une valeur donnée de x et présenterons des concepts liés à ANOVA pour la situation actuelle. Enfin, nous montrerons comment les logiciels statistiques permettent d’exécuter rapidement les calculs présentés dans cette partie.
, ainsi que l’inférence pour la réponse moyenne à une valeur x donnée. Nous discuterons ensuite des intervalles de prévision et de tolérance pour les réponses à une valeur donnée de x et présenterons des concepts liés à ANOVA pour la situation actuelle. Enfin, nous montrerons comment les logiciels statistiques permettent d’exécuter rapidement les calculs présentés dans cette partie.
