7.1.5 Utilisation du calcul statistique
Les exemples présentés dans cette section ont sans doute donné l’impression que les calculs étaient effectués « à la main ». En réalité, ces calculs sont presque toujours effectués à l’aide d’un logiciel d’analyse statistique. La régression d’une droite par la méthode des moindres carrés est généralement effectuée au moyen d’un programme de régression. La plupart du temps, ces programmes calculent aussi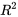 
et disposent d’une option qui permet de calculer et de tracer les résidus.
Ce cours utilise la programmation en Python et Jupyter Notebooks comme plateforme de calcul statistique, mais il existe de nombreuses autres plateformes. Des captures d’écran annotées sont souvent incluses pour montrer comment Python formate et affiche ses résultats.
La capture d’écran 7.1.5.1, qui provient de notre site GitHub, présente une analyse des données de pression et de densité de l’exemple du module 7.1.1. Cette analyse reprend largement ce que nous avons fait au cours de cette partie. Elle peut être consultée ou téléchargée (comme d’habitude) sous la partie 7 d’Intro Statistical Methods for Engineering ou sur le site GitHub spécial pour la partie 7.
Vous pouvez également ouvrir un environnement informatique interactif pour travailler avec le Jupyter Notebook en utilisant Python sur le site Binder grâce au site GitHub spécial pour l’exemple de la partie 7. Cliquez ICI pour aller au site Binder (qui se trouve à ).
La bibliothèque Statsmodels de Python que nous utilisons offre à ses utilisateurs bien plus de possibilités d’analyse pour la régression des courbes des moindres carrés que ce qui a été discuté jusqu’à présent. Ainsi, votre compréhension de la capture d’écran sera limitée. Vous devriez cependant être en mesure de repérer les valeurs des principales
statistiques de synthèse présentées ici.
The regression equation is density = 2.375 + 4.867e-05 *pressure
Results: Ordinary least squares
===================================================================
Model: OLS Adj. R-squared: 0.981
Dependent Variable: density AIC: -73.0762
Date: 2024-01-30 15:06 BIC: -71.6601
No. Observations: 15 Log-Likelihood: 38.538
Df Model: 1 F-statistic: 717.1
Df Residuals: 13 Prob (F-statistic): 9.31e-13
R-squared: 0.982 Scale: 0.00039636
---------------------------------------------------------------------
Coef. Std.Err. t P>|t| [0.025 0.975]
---------------------------------------------------------------------
Intercept 2.3750 0.0121 197.0079 0.0000 2.3490 2.4010
pressure 0.0000 0.0000 26.7780 0.0000 0.0000 0.0001
-------------------------------------------------------------------
Omnibus: 2.101 Durbin-Watson: 1.682
Prob(Omnibus): 0.350 Jarque-Bera (JB): 0.427
Skew: 0.137 Prob(JB): 0.808
Kurtosis: 3.780 Condition No.: 15556
===================================================================
ANOVA table
df sum_sq mean_sq F PR(>F) pressure 1.0 0.284213 0.284213 717.060422 9.306841e-13 Residual 13.0 0.005153 0.000396 NaN NaN
pressure density Fit StDev Fit Residual St Resid 0 2000 2.486 2.472333 0.008903 0.013667 0.767491 1 2000 2.479 2.472333 0.008903 0.006667 0.374386 2 2000 2.472 2.472333 0.008903 -0.000333 -0.018719 3 4000 2.558 2.569667 0.006296 -0.011667 -0.617705 4 4000 2.570 2.569667 0.006296 0.000333 0.017649 5 4000 2.580 2.569667 0.006296 0.010333 0.547110 6 6000 2.646 2.667000 0.005140 -0.021000 -1.091834 7 6000 2.657 2.667000 0.005140 -0.010000 -0.519921 8 6000 2.653 2.667000 0.005140 -0.014000 -0.727889 9 8000 2.724 2.764333 0.006296 -0.040333 -2.135495 10 8000 2.774 2.764333 0.006296 0.009667 0.511813 11 8000 2.808 2.764333 0.006296 0.043667 2.311982 12 10000 2.861 2.861667 0.008903 -0.000667 -0.037439 13 10000 2.879 2.861667 0.008903 0.017333 0.973403 14 10000 2.858 2.861667 0.008903 -0.003667 -0.205912