7.1.4 Mises en garde relatives à l’utilisation de la régression linéaire des moindres carrés
Les méthodes présentées dans cette section sont des outils très utiles lorsqu’elles sont appliquées judicieusement. Il convient de formuler quelques remarques supplémentaires afin de prévenir certaines erreurs de logique.
r exprime uniquement
l’association linéaire
La première mise en garde concerne la corrélation. Il convient de rappeler que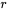 
exprime uniquement la relation linéaire entre 
et 
. Il est parfaitement possible d’avoir une forte relation non linéaire entre x et y tout en ayant une valeur de 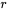proche de 0. En fait,
notre deuxième exemple illustre parfaitement cette situation. La résistance à la compression est fortement liée à la teneur en phosphate d’ammonium, mais 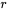= −0,005, soit très proche de 0, pour l’ensemble des données du tableau 7.1.3.1.
Corrélation et
causalitéLa deuxième mise en garde est en fait une reformulation d’une mise en garde implicite faite au début de cette discussion : la corrélation n’indique pas nécessairement un lien de causalité. Il est possible d’observer une forte corrélation entre x et y dans une étude d’observation sans pour autant que x soit à l’origine de y ou vice versa. Il se peut qu’une autre variable (par exemple, z) régisse le système étudié et provoque des changements simultanés dans x et y.
L’influence
des observations
extrêmes
La dernière mise en garde est que ,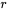 
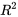et la régression des moindres carrés peuvent être considérablement perturbés par quelques données aberrantes. Par exemple, la figure 7.1.4.1 indique l’âge et la taille de 36 étudiant.e.s d’un cours de statistiques élémentaires.
Quand les gens entrent à l’université, il n’y a plus vraiment de relation utile entre l’âge et la taille. Néanmoins, la corrélation entre l’âge et la taille est de 0,73. Cette valeur assez importante est obtenue essentiellement en raison d’un seul point de données. Si l’on retire de l’ensemble des données le point correspondant à l’étudiant de 30 ans qui mesure 6 pieds 8 pouces, la corrélation tombe à 0,03.
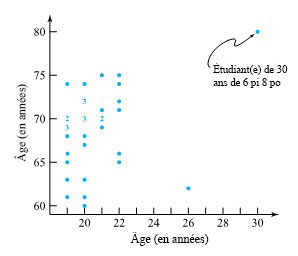
Pour éviter d’être induit en erreur par ce type de phénomène, il faut prendre l’habitude de représenter les données d’autant de façons différentes qu’il est nécessaire pour se faire une idée de la façon dont elles sont structurées. Même un simple diagramme en boîte des données relatives à l’âge ou à la taille aurait permis de dire que les données relatives à l’étudiant de 30 ans de la figure 7.1.4.1 sont aberrantes. On aurait alors pu supposer que ce point de données influençait fortement 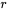et toute courbe pouvant de régression obtenue par la méthode des moindres carrés.