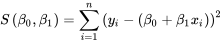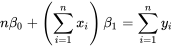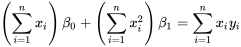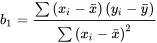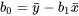7.1.1 : Application de la méthode des moindres carrés

C. Bassim et Bryan Lee

7.1.1 : Application de la méthode des moindres carrés

Exemple 7.1.1.1 : Pression de pressage et densité des échantillons d’un composé céramique

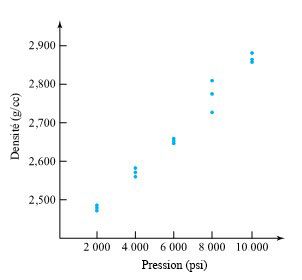
Benson, Locher et Watkins ont étudié les effets de différentes pressions de pressage sur la densité d’échantillons cylindriques fabriqués par pressage à sec d’un composé céramique. Un mélange d’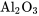 $\mathrm{Al}_2 \mathrm{O}_3$ , d’alcool polyvinylique et d’eau a été préparé, séché pendant une nuit, broyé et tamisé pour obtenir des grains d’une taille de 100 mesh. Ceux-ci ont été pressés dans des cylindres à des pressions allant de 2 000 psi à 10 000 psi, puis la densité des cylindres a été calculée. Les données obtenues sont présentées dans le tableau 7.1.1.1, et un nuage de points simple de ces données est présenté dans la figure 7.1.1.1.

Figure 7.1.1.1 : Nuage de points de la densité en fonction de la pression de pressage

Tableau 7.1.1.1 : Pressions de pressage et densité
de l’échantillon résultant

Il est très facile d’imaginer une ligne droite passant par les points de la figure 7.1.1.1 . Cette droite pourrait alors être utilisée pour illustrer comment la densité varie en fonction de la pression. La méthode des moindres carrés permet de choisir la « meilleure » droite pour décrire les données.

DÉFINITION Méthode des moindres carrés

EXPRESSION 7.1.1.1

La méthode des moindres carrés pour ajuster une équation pour y à un ensemble de données de n points consister à trouver les paramètres de l’équation qui minimisent la somme

$\sum_{i=1}^n\left(y_i-\hat{y}_i\right)^2$

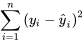
où 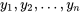$y_1, y_2, \ldots, y_n$ sont les réponses observées et 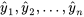$\hat{y}_1, \hat{y}_2, \ldots, \hat{y}_n$ sont les réponses correspondantes prédites (ou ajustées) par l’équation.

Selon la définition 7.1.1.1, dans le cadre de l’ajustement d’une droite aux données (x, y), il faut choisir une pente et une ordonnée à l’origine de manière à minimiser la somme des carrés des distances verticales entre les points (x, y) et la droite en question. Cette notion est illustrée de façon générique à la figure 7.1.1.2 pour un ensemble fictif de cinq données. (C’est la somme des carrés des cinq différences indiquées qu’il faut minimiser.)

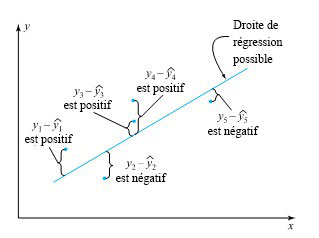
Figure 7.1.1.2 Cinq points de données (x, y) et une possible
droite de régression.

Selon la forme de l’équation (7.1.0.1), l’équation pour la régression d’une droite est

$\hat{y} = \beta_0 + \beta_1 x$

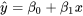
Par conséquent, l’expression à minimiser en choisissant la pente 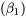$\left(\beta_1\right)$ , et l’ordonnée à l’origine 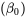$\left(\beta_0\right)$ est la suivante :

7.1.1.2 $S\left(\beta_0, \beta_1\right) = \sum_{i=1}^n\left(y_i - \left(\beta_0 + \beta_1 x_i\right)\right)^2$

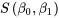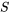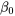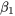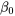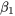La minimisation de la fonction de deux variables $S\left(\beta_0, \beta_1\right)$ est un exercice de calcul différentiel. On met les dérivées partielles de $S$ par rapport à $\beta_0$ et à $\beta_1$ égales à zéro, puis on résout le système de deux équations pour obtenir $\beta_0$ et $\beta_1$ . Les équations ainsi obtenues sont

7.1.1.3 $n \beta_0 + \left(\sum_{i=1}^n x_i\right) \beta_1 = \sum_{i=1}^n y_i$

et

7.1.1.4 $\left(\sum_{i=1}^n x_i\right) \beta_0 + \left(\sum_{i=1}^n x_i^2\right) \beta_1 = \sum_{i=1}^n x_i y_i$

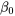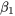Pour des raisons obscures, les équations 7.1.1.3 et 7.1.1.4 sont parfois appelées équations normales (dans le sens de « perpendiculaire ») pour la régression d’une droite. Ce sont deux équations linéaires à deux inconnues qu’on peut résoudre assez facilement pour $\beta_0$ et $\beta_1$ (à condition qu’il y ait au moins deux x_i différents dans l’ensemble de données). En résolvant les équations 7.1.1.3 et 7.1.1.4, on obtient les valeurs de [latex]\beta_0[/latex] et 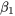$\beta_1$ suivantes :

Pente de la droite des moindres carrés, $\beta_1$ 7.1.1.5

$b_1 = \frac{\sum\left(x_i - \bar{x}\right)\left(y_i - \bar{y}\right)}{\sum\left(x_i - \bar{x}\right)^2}$

et

Ordonnée à l’origine de la droite des moindres carrés, $\beta_0$ 7.1.1.6

$b_0 = \bar{y} - b_1 \bar{x}$

Soulignons ici la convention de notation. La pente et l’ordonnée à l’origine qui minimisent 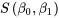$S\left(\beta_0, \beta_1\right)$ sont désignées non pas par les paramètres β, mais par les paramètres 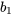$b_1$ et $b_0$ .

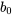Remarque concernant l’expression (7.1.1.5) : la pratique assez courante qui a été suivie (et l’abus de notation de la somme) consiste à ne pas indiquer la variable de sommation (i) ni son intervalle (de 1 à n).

Exemple 7.1.1.2 (suite)

Il est possible de vérifier que les données du tableau 7.1.1.1 donnent les résultats sommaires suivants :

$\begin{aligned} \sum x_i = & 2 000+2 000+\cdots+10 000 = 90 000, \\ \text { donc } \bar{x} = & \frac{90 000}{15 } = 6 000 \\ \sum\left(x_i - \bar{x}\right)^2 = & (2 000 - 6 000)^2 + (2 000 - 6 000)^2 + \cdots \\ \sum y_i = & 2,486 + 2,479 + \cdots + 2,858 = 40,005 \\ \text { donc } \bar{y} = & \frac{40,005}{15 } = 2,667 \\ \sum\left(y_i - \bar{y}\right)^2 = & (2,486 - 2,667)^2 + (2,479 - 2,667)^2 + \cdots+ \\ & (2,858 - 2,667)^2 = 0,289366 \\ \sum\left(x_i - \bar{x}\right)\left(y_i - \bar{y}\right) = & (2 000 - 6 000)(2,486 - 2,667) + \cdots+ \\ & (10 000 - 6 000)(2,858 - 2,667) = 5 840 \end{aligned}$

Les équations 7.1.1.5 et 7.1.1.6 donnent alors la pente et l’ordonnée à l’origine des moindres carrés, 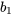$b_1$ et $b_0$ :

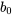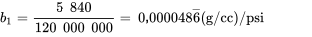$b_1 = \frac{5 840}{120 000 000} = 0,000048 \overline{6 } (\mathrm{~g} / \mathrm{cm3}) / \mathrm{psi}$ }) / \mathrm{psi}

et

$b_0 = 2,667-(0,000048 \overline{6 })(6 000) = 2,375 \mathrm{~g} / \mathrm{cm3}$

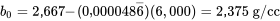
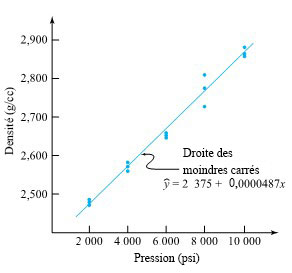
La figure 7.1.1.3 montre la droite des moindres carrés

$\hat{y} = 2,375 + 0,0000487 x$

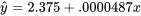
tracée sur le nuage de points (x, y) tiré du tableau 7.1.1.1.

Interprétation de
la pente de la droite des moindres carrésIl convient de noter que la pente sur ce graphique, 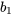$b_1$ ≈ 0,0000487 (g/cm³)/psi, correspond physiquement à l’augmentation (approximative) de y (densité) qui accompagne une augmentation d’une unité (1 psi) de x (pression).

Interprétation de l’ordonnée à l’origine et extrapolation prudenteL’ordonnée à l’origine du tracé, 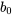$b_0$ = 2,375 g/cm³, positionne la droite verticalement et est la valeur à laquelle la droite coupe l’axe des y. Cependant, il ne faut probablement pas l’interpréter comme la densité qui correspondrait à une pression de x = 0 psi. Le fait est que la relation raisonnablement linéaire constatée pour des pressions comprises entre 2 000 et 10 000 psi pourrait bien ne pas s’appliquer à des pressions plus grandes ou plus petites Considérer 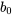$b_0$ comme la densité obtenue lorsque la pression est 0 revient à extrapoler en dehors de la plage de données utilisée pour obtenir la droite de régression, ce qu’il faut toujours faire avec une extrême prudence.

Figure 7.1.1.3 Nuage de points des données de pression/densité et droite des moindres carrés.

Comme l’indique la déﬁnition 7.1.1.1, la valeur de y sur la droite des moindres carrés correspondant à un x donné peut être appelée une valeur ajustée ou prédite. Elle peut être utilisée pour représenter le comportement probable de y pour ce x.

Exemple 7.1.1.3 (suite)

Trouvons la densité type correspondant à une pression de 4 000 psi et à une pression de 5 000 psi. Tout d’abord, si l’on considère que x = 4 000, une manière simple de représenter un y type est de
noter que pour les trois points de données à x = 4 000,

$\bar{y} = \frac{1 }{3 }(2,558 + 2,570 + 2,580) = 2,5693 \mathrm{~g} / \mathrm{cm3}$

et donc d’utiliser cette valeur comme valeur représentative. Mais en supposant que y soit effectivement approximativement linéairement proportionnelle à x, la valeur ajustée

$\hat{y} = 2,375 + 0,000048 \overline{6 } (4 000) = 2,5697 \mathrm{~g} / \mathrm{cm3}$

pourrait être encore plus représentative de la densité moyenne pour une pression de 4 000 psi.

InterpolationEn examinant la situation, on constate qu’il n’y a pas de données pour x = 5 000 psi. La seule chose que l’on puisse faire pour représenter la densité à cette pression est de se demander
si l’interpolation est raisonnable d’un point de vue physique. Si c’est le cas, la valeur ajustée

$\hat{y} = 2,375 + 0,000048 \overline{6 } (5 000) = 2,6183 \mathrm{~g} / \mathrm{cm3}$

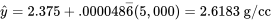
peut être utilisée pour représenter la densité à une pression de 5 000 psi.

7.1.1 : Application de la méthode des moindres carrés

Licence

Partagez ce livre