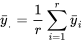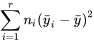6.3.2 Test F de l’ANOVA à un facteur
La méthode standard de test de l’hypothèse 6.3.2.6
.
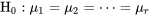
.
pour l’absence de différence entre  moyennes s’opposant à l’hypothèse
moyennes s’opposant à l’hypothèse
 moyennes s’opposant à l’hypothèse
moyennes s’opposant à l’hypothèse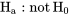
.
est essentiellement basée sur la comparaison entre la mesure de la variabilité des moyennes d’échantillons et la variance d’échantillons pondérée, 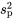 . Certaines conventions de notation supplémentaires sont nécessaires pour pouvoir présenter pleinement cette méthode.
. Certaines conventions de notation supplémentaires sont nécessaires pour pouvoir présenter pleinement cette méthode.
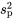 . Certaines conventions de notation supplémentaires sont nécessaires pour pouvoir présenter pleinement cette méthode.
. Certaines conventions de notation supplémentaires sont nécessaires pour pouvoir présenter pleinement cette méthode..
Dans la suite de cet ouvrage, il sera souvent plus pratique d’utiliser des notations globales pour les mesures de la partie 2 (moyennes et variances d’échantillons) appliquées aux données des études multi-échantillons, en laissant de côté le nombre total d’échantillons ( ). La lettre
). La lettre  dénuée d’indice a déjà été utilisée pour remplacer
dénuée d’indice a déjà été utilisée pour remplacer 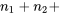
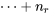 , le nombre d’observations disponibles, en ignorant le nombre total d’échantillons (
, le nombre d’observations disponibles, en ignorant le nombre total d’échantillons ( ). Cette convention sera désormais expressément étendue aux statistiques calculées à partir des
). Cette convention sera désormais expressément étendue aux statistiques calculées à partir des  réponses. Pour plus de clarté, cela sera énoncé sous forme de définition.
réponses. Pour plus de clarté, cela sera énoncé sous forme de définition.
 ). La lettre
). La lettre  dénuée d’indice a déjà été utilisée pour remplacer
dénuée d’indice a déjà été utilisée pour remplacer 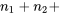
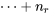 , le nombre d’observations disponibles, en ignorant le nombre total d’échantillons (
, le nombre d’observations disponibles, en ignorant le nombre total d’échantillons ( ). Cette convention sera désormais expressément étendue aux statistiques calculées à partir des
). Cette convention sera désormais expressément étendue aux statistiques calculées à partir des  réponses. Pour plus de clarté, cela sera énoncé sous forme de définition.
réponses. Pour plus de clarté, cela sera énoncé sous forme de définition..
DÉFINITION 6.3.2.1 Convention de notation pour les études multi-échantillons
Dans les études multi-échantillons, les symboles représentant des tailles ou des statistiques d’échantillons qui apparaîtront sans indice ni point seront considérées comme tenant compte de toutes les réponses disponibles, en combinant tous les échantillons.
.
Ainsi,  représentera le nombre total de points de données (même dans une étude à
représentera le nombre total de points de données (même dans une étude à  échantillons),
échantillons), 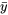 la moyenne du grand échantillon de la réponse
la moyenne du grand échantillon de la réponse 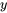 , et
, et 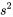 une variance du grand échantillon calculée en combinant tous les échantillons.
une variance du grand échantillon calculée en combinant tous les échantillons.
 représentera le nombre total de points de données (même dans une étude à
représentera le nombre total de points de données (même dans une étude à  échantillons),
échantillons), 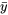 la moyenne du grand échantillon de la réponse
la moyenne du grand échantillon de la réponse 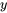 , et
, et 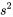 une variance du grand échantillon calculée en combinant tous les échantillons.
une variance du grand échantillon calculée en combinant tous les échantillons..
Pour les besoins présents (construire une variable pour tester l’hypothèse 6.3.1.6), il faut utiliser 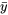 , la moyenne du grand échantillon. Il est important de reconnaître que
, la moyenne du grand échantillon. Il est important de reconnaître que 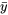 et
et
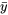 , la moyenne du grand échantillon. Il est important de reconnaître que
, la moyenne du grand échantillon. Il est important de reconnaître que 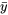 et
et.
6.3.2.1 Moyenne (non pondérée) des moyennes deéchantillons
.
ne sont pas forcément identiques, à moins que tous les échantillons aient la même taille. En effet, lorsque la taille des échantillons varie, 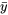 est la moyenne arithmétique (non pondérée) des valeurs de données brutes
est la moyenne arithmétique (non pondérée) des valeurs de données brutes 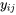 , et la moyenne pondérée des moyennes d’échantillons
, et la moyenne pondérée des moyennes d’échantillons 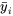 . En contrepartie,
. En contrepartie, 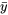 est la moyenne arithmétique (non pondérée) des moyennes d’échantillons
est la moyenne arithmétique (non pondérée) des moyennes d’échantillons 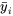 , et la moyenne pondérée des valeurs de données brutes
, et la moyenne pondérée des valeurs de données brutes 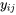 . Par exemple, dans le cas très simple où
. Par exemple, dans le cas très simple où 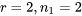 et
et 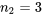 ,
,
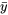 est la moyenne arithmétique (non pondérée) des valeurs de données brutes
est la moyenne arithmétique (non pondérée) des valeurs de données brutes 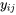 , et la moyenne pondérée des moyennes d’échantillons
, et la moyenne pondérée des moyennes d’échantillons 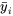 . En contrepartie,
. En contrepartie, 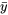 est la moyenne arithmétique (non pondérée) des moyennes d’échantillons
est la moyenne arithmétique (non pondérée) des moyennes d’échantillons 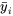 , et la moyenne pondérée des valeurs de données brutes
, et la moyenne pondérée des valeurs de données brutes 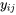 . Par exemple, dans le cas très simple où
. Par exemple, dans le cas très simple où 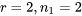 et
et 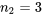 ,
,.
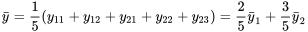
.
alors que
.
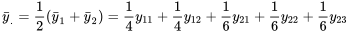
.
et qu’en général, 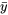 et
et 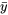 ne sont pas identiques.
ne sont pas identiques.
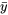 et
et 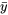 ne sont pas identiques.
ne sont pas identiques..
D’après l’hypothèse 6.3.1.6 (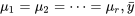 est une estimation naturelle de la moyenne commune. (Toutes les distributions sous-jacentes sont les mêmes; les données disponibles sont donc considérées, à juste titre, non pas comme
est une estimation naturelle de la moyenne commune. (Toutes les distributions sous-jacentes sont les mêmes; les données disponibles sont donc considérées, à juste titre, non pas comme  échantillons différents, mais plutôt comme un échantillon unique de taille
échantillons différents, mais plutôt comme un échantillon unique de taille  .) Les différences
.) Les différences 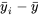 sont donc des indicateurs de différences potentielles parmi les
sont donc des indicateurs de différences potentielles parmi les 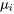 . Il est pratique de résumer la taille de ces différences
. Il est pratique de résumer la taille de ces différences 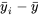 en prenant une sorte de somme de leurs carrés :
en prenant une sorte de somme de leurs carrés :
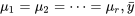 est une estimation naturelle de la moyenne commune. (Toutes les distributions sous-jacentes sont les mêmes; les données disponibles sont donc considérées, à juste titre, non pas comme
est une estimation naturelle de la moyenne commune. (Toutes les distributions sous-jacentes sont les mêmes; les données disponibles sont donc considérées, à juste titre, non pas comme  échantillons différents, mais plutôt comme un échantillon unique de taille
échantillons différents, mais plutôt comme un échantillon unique de taille  .) Les différences
.) Les différences 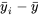 sont donc des indicateurs de différences potentielles parmi les
sont donc des indicateurs de différences potentielles parmi les 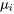 . Il est pratique de résumer la taille de ces différences
. Il est pratique de résumer la taille de ces différences 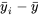 en prenant une sorte de somme de leurs carrés :
en prenant une sorte de somme de leurs carrés :.
6.3.2.2
.
On peut considérer la statistique 6.3.2.2 soit comme une somme pondérée des quantités 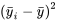 , soit comme une somme non pondérée, avec un terme de la somme pour chaque point de données brutes, donc
, soit comme une somme non pondérée, avec un terme de la somme pour chaque point de données brutes, donc 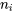 termes
termes 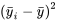 . La quantité 6.3.2.2 est une mesure de la variation inter-échantillons des données. Pour un ensemble donné de tailles d’échantillons, plus cette quantité est grande, plus la variation entre les moyennes d’échantillons
. La quantité 6.3.2.2 est une mesure de la variation inter-échantillons des données. Pour un ensemble donné de tailles d’échantillons, plus cette quantité est grande, plus la variation entre les moyennes d’échantillons 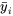 est grande.
est grande.
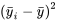 , soit comme une somme non pondérée, avec un terme de la somme pour chaque point de données brutes, donc
, soit comme une somme non pondérée, avec un terme de la somme pour chaque point de données brutes, donc 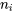 termes
termes 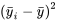 . La quantité 6.3.2.2 est une mesure de la variation inter-échantillons des données. Pour un ensemble donné de tailles d’échantillons, plus cette quantité est grande, plus la variation entre les moyennes d’échantillons
. La quantité 6.3.2.2 est une mesure de la variation inter-échantillons des données. Pour un ensemble donné de tailles d’échantillons, plus cette quantité est grande, plus la variation entre les moyennes d’échantillons 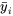 est grande.
est grande..
Pour construire une variable à tester pour l’hypothèse 6.3.1.6, il suffit de diviser la mesure 6.3.2.2 par 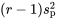 . On obtient alors :
. On obtient alors :
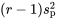 . On obtient alors :
. On obtient alors :.
6.3.2.3 Statistique de test de l’ANOVA à un facteur pour l’égalité de  moyennes
moyennes
 moyennes
moyennes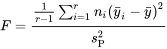
.
Le fait est que si 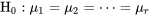 est vraie, d’après les hypothèses du modèle à un facteur, cette statistique présente une distribution
est vraie, d’après les hypothèses du modèle à un facteur, cette statistique présente une distribution 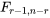 . L’hypothèse d’égalité de
. L’hypothèse d’égalité de  moyennes peut donc être testée à l’aide de l’équation 6.3.2.3 et d’une distribution
moyennes peut donc être testée à l’aide de l’équation 6.3.2.3 et d’une distribution 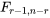 de référence, où les grandes valeurs observées de
de référence, où les grandes valeurs observées de 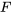 permettent d’infirmer
permettent d’infirmer 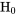 et de confirmer
et de confirmer 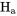 : pas
: pas 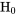 .
.
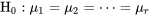 est vraie, d’après les hypothèses du modèle à un facteur, cette statistique présente une distribution
est vraie, d’après les hypothèses du modèle à un facteur, cette statistique présente une distribution 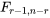 . L’hypothèse d’égalité de
. L’hypothèse d’égalité de  moyennes peut donc être testée à l’aide de l’équation 6.3.2.3 et d’une distribution
moyennes peut donc être testée à l’aide de l’équation 6.3.2.3 et d’une distribution 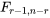 de référence, où les grandes valeurs observées de
de référence, où les grandes valeurs observées de 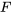 permettent d’infirmer
permettent d’infirmer 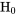 et de confirmer
et de confirmer 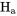 : pas
: pas 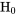 .
..
Exemple 6.3.2.1 Étude sur la compression du béton (suite)
Reprenons l’exemple de l’étude de résistance à la compression du béton d’Armstrong, Babb et Campen. Nous avions 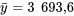 . et les 8 moyennes d’échantillons
. et les 8 moyennes d’échantillons 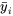 présentent diffèrent de cette valeur par les écarts donnés dans le tableau 6.3.2.1.
présentent diffèrent de cette valeur par les écarts donnés dans le tableau 6.3.2.1.
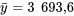 . et les 8 moyennes d’échantillons
. et les 8 moyennes d’échantillons 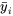 présentent diffèrent de cette valeur par les écarts donnés dans le tableau 6.3.2.1.
présentent diffèrent de cette valeur par les écarts donnés dans le tableau 6.3.2.1..
Puis, étant donné que pour tout i, 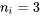 , dans cette situation :
, dans cette situation :
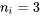 , dans cette situation :
, dans cette situation :.
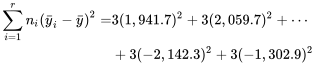
.
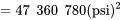
.
Pour pouvoir utiliser ce chiffre pour juger de la signification statistique, on standardise à l’aide de l’équation 6.3.2.3 afin d’obtenir la valeur observée de la statistique de test :
.
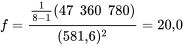
.
Il est très facile de vérifier dans les tables A1.5 (les tables F) que 20.0 est supérieur au quantile 0,999 de la distribution 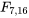 . On a donc :
. On a donc :
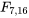 . On a donc :
. On a donc :.
<img src= »https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/e9b4dd4099f8c03b16055ccc210777db.png » alt= »\text {valeur p }=P\left[\text { une variable aléatoire } F_{7,16} \geq 20,0\right]<0,001″ title= »\text {valeur p }=P\left[\text { une variable aléatoire } F_{7,16} \geq 20,0\right]
.
Ainsi, les données permettent largement de prouver que 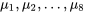 ne sont pas toutes égales.
ne sont pas toutes égales.
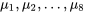 ne sont pas toutes égales.
ne sont pas toutes égales.
Tableau 6.3.2.1 Moyennes d’échantillon et écarts par rapport à \bar{y} dans l’étude de la résistance du béton
.
Pour des raisons purement pédagogiques, le test de l’ANOVA à un facteur a été présenté après les méthodes d’inférence axées sur les intervalles dans les études à  échantillons. Mais si elle doit être mise en pratique, la méthode de test d’hypothèse intervient typiquement chronologiquement avant l’estimation. En d’autres termes, le test de l’ANOVA peut permettre de déterminer en amont si les données disponibles conviennent pour différencier les moyennes de façon concluante, ou s’il faut plus de données.
échantillons. Mais si elle doit être mise en pratique, la méthode de test d’hypothèse intervient typiquement chronologiquement avant l’estimation. En d’autres termes, le test de l’ANOVA peut permettre de déterminer en amont si les données disponibles conviennent pour différencier les moyennes de façon concluante, ou s’il faut plus de données.
 échantillons. Mais si elle doit être mise en pratique, la méthode de test d’hypothèse intervient typiquement chronologiquement avant l’estimation. En d’autres termes, le test de l’ANOVA peut permettre de déterminer en amont si les données disponibles conviennent pour différencier les moyennes de façon concluante, ou s’il faut plus de données.
échantillons. Mais si elle doit être mise en pratique, la méthode de test d’hypothèse intervient typiquement chronologiquement avant l’estimation. En d’autres termes, le test de l’ANOVA peut permettre de déterminer en amont si les données disponibles conviennent pour différencier les moyennes de façon concluante, ou s’il faut plus de données.