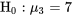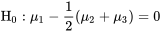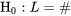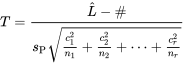6.3.1 Tests d’hypothèse et études multi-échantillons
De même que de nombreuses quantités peuvent être à estimer dans une étude multi-échantillon, il peut y avoir de nombreux tests d’hypothèse à effectuer. On peut par exemple souhaiter obtenir des valeurs  pour des hypothèses comme :
pour des hypothèses comme :
 pour des hypothèses comme :
pour des hypothèses comme :.
6.3.1 .16.3.1.26.3.1.3
.
Les méthodes d’intervalle de confiance abordées à la section 6.2 ont des méthodes équivalentes pour les tests d’hypothèse qui, comme les trois ci-dessus, impliquent une combinaison linéaire des moyennes 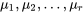 .
.
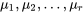 .
..
En général (sous le modèle à un facteur standard), soit :
.
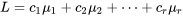
.
Alors, l’hypothèse
6.3.1.4
.
peut être testée à l’aide de la statistique de test suivante :
.
6.3.1.5.
.
et d’une distribution 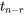 de référence. Pour adapter cet énoncé aux hypothèses de type 6.3.1.1 à 6.3.1.3, il suffit de choisir les
de référence. Pour adapter cet énoncé aux hypothèses de type 6.3.1.1 à 6.3.1.3, il suffit de choisir les 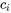 et # correctement.
et # correctement.
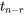 de référence. Pour adapter cet énoncé aux hypothèses de type 6.3.1.1 à 6.3.1.3, il suffit de choisir les
de référence. Pour adapter cet énoncé aux hypothèses de type 6.3.1.1 à 6.3.1.3, il suffit de choisir les 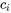 et # correctement.
et # correctement..
Mais la méthode de test d’hypothèses le plus souvent associée au modèle normal à un facteur ne convient pas aux hypothèses de type 6.3.1.4. La méthode la plus courante repose plutôt sur l’hypothèse selon laquelle les  moyennes sous-jacentes sont égales. En symboles, cela équivaut à :
moyennes sous-jacentes sont égales. En symboles, cela équivaut à :
 moyennes sous-jacentes sont égales. En symboles, cela équivaut à :
moyennes sous-jacentes sont égales. En symboles, cela équivaut à :.
6.3.1.6
.
Si on travaille à partir des hypothèses du modèle à un facteur, l’hypothèse 6.3.1.6 revient à affirmer que les  distributions sous-jacentes sont essentiellement les mêmes – autrement dit, « il n’y a aucune différence entre les processus ».
distributions sous-jacentes sont essentiellement les mêmes – autrement dit, « il n’y a aucune différence entre les processus ».
 distributions sous-jacentes sont essentiellement les mêmes – autrement dit, « il n’y a aucune différence entre les processus ».
distributions sous-jacentes sont essentiellement les mêmes – autrement dit, « il n’y a aucune différence entre les processus »..
L’hypothèse 6.3.1.6 peut être considérée comme l’égalité simultanée des 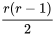 paires de moyennes – c’est-à-dire qu’elle est équivalente à l’affirmation selon laquelle, simultanément,
paires de moyennes – c’est-à-dire qu’elle est équivalente à l’affirmation selon laquelle, simultanément,
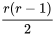 paires de moyennes – c’est-à-dire qu’elle est équivalente à l’affirmation selon laquelle, simultanément,
paires de moyennes – c’est-à-dire qu’elle est équivalente à l’affirmation selon laquelle, simultanément,.
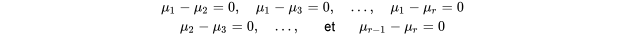
.
Cet énoncé n’est pas sans rappeler ce qui a été dit sur les intervalles de confiance simultanés de la section précédente (à savoir la méthode de Tukey). D’ailleurs, l’une des façons de juger de la signification statistique d’un ensemble de données à  échantillons, en ayant pour référence l’hypothèse 6.3.1.6, est d’appliquer la méthode de Tukey d’estimation d’intervalles simultanés et de noter si tous les intervalles de différences de moyennes incluent la valeur 0. Si c’est le cas pour tous, la valeur
échantillons, en ayant pour référence l’hypothèse 6.3.1.6, est d’appliquer la méthode de Tukey d’estimation d’intervalles simultanés et de noter si tous les intervalles de différences de moyennes incluent la valeur 0. Si c’est le cas pour tous, la valeur  associée est supérieure à 1 moins le niveau de confiance simultané. Sinon, la valeur
associée est supérieure à 1 moins le niveau de confiance simultané. Sinon, la valeur  associée est inférieure à 1 moins le niveau de confiance simultané. (Par exemple, si les intervalles simultanés de
associée est inférieure à 1 moins le niveau de confiance simultané. (Par exemple, si les intervalles simultanés de 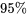 incluent tous 0, alors aucune différence entre les moyennes n’est définitivement établie et la valeur
incluent tous 0, alors aucune différence entre les moyennes n’est définitivement établie et la valeur  correspondante est supérieure à 0,05.)
correspondante est supérieure à 0,05.)
 échantillons, en ayant pour référence l’hypothèse 6.3.1.6, est d’appliquer la méthode de Tukey d’estimation d’intervalles simultanés et de noter si tous les intervalles de différences de moyennes incluent la valeur 0. Si c’est le cas pour tous, la valeur
échantillons, en ayant pour référence l’hypothèse 6.3.1.6, est d’appliquer la méthode de Tukey d’estimation d’intervalles simultanés et de noter si tous les intervalles de différences de moyennes incluent la valeur 0. Si c’est le cas pour tous, la valeur  associée est supérieure à 1 moins le niveau de confiance simultané. Sinon, la valeur
associée est supérieure à 1 moins le niveau de confiance simultané. Sinon, la valeur  associée est inférieure à 1 moins le niveau de confiance simultané. (Par exemple, si les intervalles simultanés de
associée est inférieure à 1 moins le niveau de confiance simultané. (Par exemple, si les intervalles simultanés de 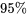 incluent tous 0, alors aucune différence entre les moyennes n’est définitivement établie et la valeur
incluent tous 0, alors aucune différence entre les moyennes n’est définitivement établie et la valeur  correspondante est supérieure à 0,05.)
correspondante est supérieure à 0,05.).
Nous admettons privilégier l’estimation plutôt que les tests d’hypothèse. Conséquence : une tendance à déduire une approximation de la valeur  pour l’hypothèse 6.3.1.6 en utilisant la méthode de Tukey. Mais une méthode de test plus connue pour l’hypothèse 6.3.1.6 mérite également d’être abordée : l’analyse de la variance à un facteur.
pour l’hypothèse 6.3.1.6 en utilisant la méthode de Tukey. Mais une méthode de test plus connue pour l’hypothèse 6.3.1.6 mérite également d’être abordée : l’analyse de la variance à un facteur.
 pour l’hypothèse 6.3.1.6 en utilisant la méthode de Tukey. Mais une méthode de test plus connue pour l’hypothèse 6.3.1.6 mérite également d’être abordée : l’analyse de la variance à un facteur.
pour l’hypothèse 6.3.1.6 en utilisant la méthode de Tukey. Mais une méthode de test plus connue pour l’hypothèse 6.3.1.6 mérite également d’être abordée : l’analyse de la variance à un facteur..
Il semble étrange, à ce stade, qu’un test de moyennes porte un nom qui mette apparemment l’accent sur la variance. Ce terme se justifie par le fait que ce test est lié à une façon très pratique de considérer la répartition de la variabilité globale d’une variable de réponse. Il s’agit du test F de l’ANOVA à un facteur.