2.1.3 Tableaux de fréquences et histogrammes
Exemple 2.1.3.1. Faux-rond des engrenages empilés
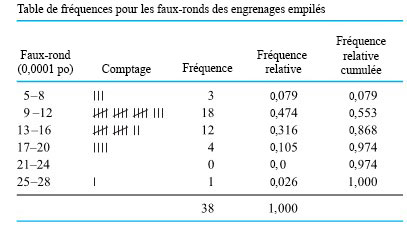
Le tableau 2.1.3.1 constitue une table des fréquences pour le faux-rond des engrenages empilés. Les valeurs de fréquence relative sont obtenues en divisant les entrées dans la colonne des fréquences par 38, le nombre total de points de données. Les entrées de la colonne de fréquence relative cumulées se calculent en divisant le total d’une classe donnée et de toutes les classes précédentes par le nombre total de points de données. (Sauf arrondissement, il s’agit de la somme des fréquences relatives sur la même ligne et au-dessus d’une fréquence relative cumulative). La colonne de points indique le même type d’informations sur la forme de la distribution que ce qu’on obtient d’un diagramme de dispersion ou d’un diagramme tige et feuilles.
Choix d’un intervalle d’un tableau de fréquences
Le choix des intervalles à utiliser dans un tableau de fréquences est une subjectif (deux personnes ne choisiront pas forcément les mêmes intervalles). Cependant, il faut prendre en compte quelques points simples. Tout d’abord, pour éviter que la colonne des points ne fausse l’impression de la forme de la distribution, il convient d’utiliser des intervalles de même longueur. En outre, pour des raisons esthétiques, il est préférable de choisir des nombres ronds pour les extrémités des intervalles. Étant donné que la réduction des données brutes en tables implique généralement une agrégation (et donc une certaine perte d’informations), plus le nombre d’intervalles utilisés est élevé, plus les informations présentées dans le tableau sont détaillées. En contrepartie, pour qu’un tableau de fréquences synthétise réellement les données, il ne doit pas être encombré d’un trop grand nombre d’intervalles.
Après avoir monté un tableau de fréquences, on utilise généralement l’organisation fournie qu’il fournit pour générer un histogramme. Un histogramme (de fréquence ou de fréquence relative) est un type de diagramme à barres utilisé pour représenter la forme d’une distribution de points de données.
Exemple 2.1.2.2. Pénétration de balles de 200 grains (suite)
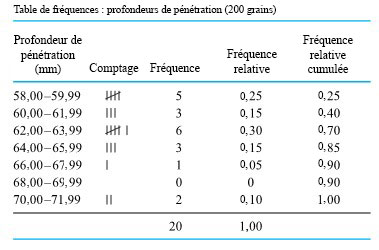
Le tableau 2.1.3.2 est un tableau de fréquences pour les profondeurs de pénétration des balles de 200 grains, et la figure 2.1.3.1 présente cette table sous forme d’histogramme.
.
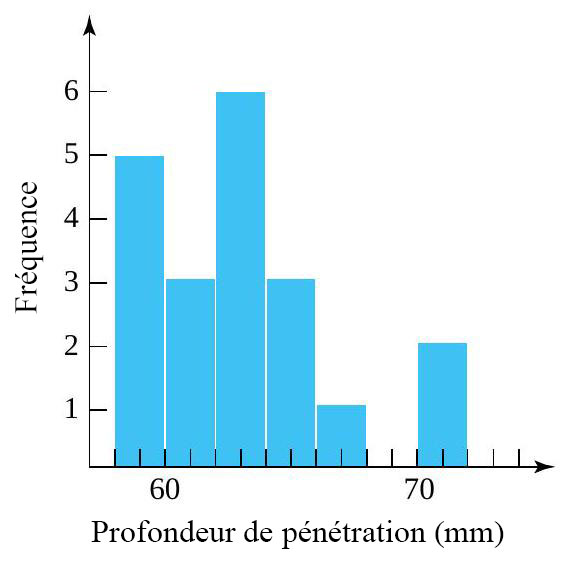
L’échelle verticale de la figure 2.1.3.1 est une échelle de fréquence, et l’histogramme est un histogramme de fréquence. En passant à la fréquence relative sur l’échelle verticale, on peut produire un histogramme de fréquence relative.
Lignes directrices pour l’élaboration d’histogrammes
Lors de l’élaboration de la figure 2.1.3.1, on a veillé à:
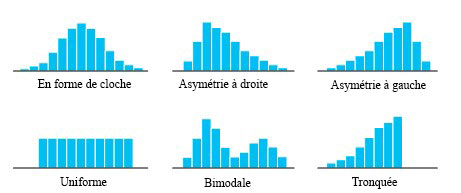
Exemples d’interprétations d’ingénierie de la forme de la distribution
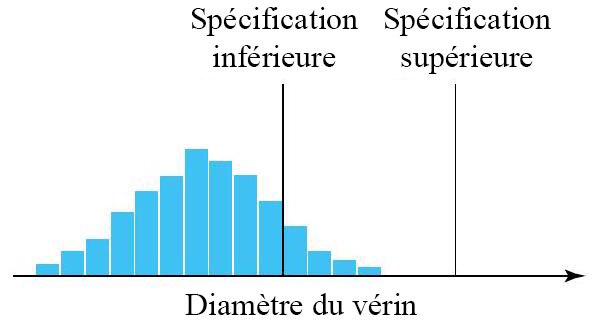
Si, par exemple, les données relatives aux diamètres des vérins métalliques usinés achetés à un fournisseur produisent un histogramme résolument bimodal (ou multimodal, avec plusieurs bosses nettes), cela suggère que l’usinage a été effectué sur plusieurs machines, ou par plusieurs opérateurs, ou à différents moments. La conséquence pratique d’un tel usinage varié est une distribution des diamètres qui présente plus de variations que celles typiques d’une production provenant d’une seule machine, d’un seul opérateur et d’une seule configuration. Par ailleurs, si l’histogramme est tronqué, cela peut suggérer que le lot de vérins a été entièrement inspecté et trié afin d’éliminer tous les vérins présentant des diamètres excessifs. Qui plus est, en indiquant les spécifications (exigences) pour le diamètre du vérin sur l’histogramme, on peut obtenir une image comme celle de la figure 2.1.3.3. Il devient alors évident que le tour qui usine les vérins doit être ajusté afin d’augmenter le diamètre typique, mais il est aussi manifeste que la variation du processus de base est si importante que cet ajustement ne parviendra pas à rendre tous les diamètres conformes aux spécifications. Avec cette constatation et sa connaissance des conséquences économiques de la non-conformité des pièces aux spécifications, l’ingénieur.e peut évaluer intelligemment d’autres possibilités d’action : trier toutes les pièces entrantes, exiger du fournisseur qu’il utilise un équipement plus précis, chercher un nouveau fournisseur, etc.