2.1.2 Diagrammes à points et diagrammes à tiges et à feuilles
Lorsqu’une étude produit une quantité faible ou modérée de données quantitatives à une seule variable, un diagramme à points (qu’on peut facilement créer avec un crayon et du papier) est souvent très révélateur. Ces diagrammes présentent chaque observation sous la forme d’un point placé, sur une droite numérique, à une position correspondant à sa valeur.
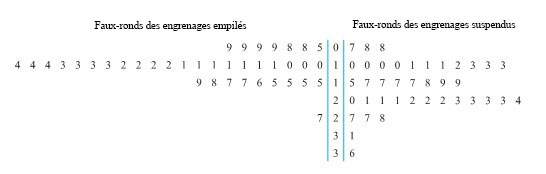
Exemple 2.1.2.1. Représentation du faux-rond des engrenages
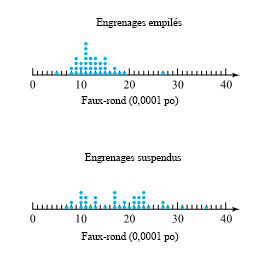
Au module 1.1, nous avons abordé un problème de traitement thermique portant sur la distorsion des engrenages empilés et des engrenages suspendus. Cette figure est reproduite ici à la figure 2.1.2.1. Il s’agit de deux diagrammes à points, l’un montrant les valeurs de faux-rond de la face de poussée pour les engrenages empilés, et l’autre, les valeurs correspondantes pour les engrenages suspendus. On voit clairement que les valeurs des engrenages empilés sont généralement plus petites et moins dispersées que celles des engrenages suspendus.
.
Exemple 2.1.2.2. Pénétration de balle à 200 grains
Sale et Thom ont comparé la profondeur de pénétration de plusieurs types de balles de calibre 0,45 tirées dans du bois de chêne à une distance de 15 pieds. Le tableau 2.1.2.1 répertorie les profondeurs de pénétration (exprimées en 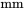 de la surface de la cible jusqu’à l’arrière des balles) pour deux types de balles. La figure 2.1.2.2 présente une paire de diagrammes à points correspondants.
de la surface de la cible jusqu’à l’arrière des balles) pour deux types de balles. La figure 2.1.2.2 présente une paire de diagrammes à points correspondants.
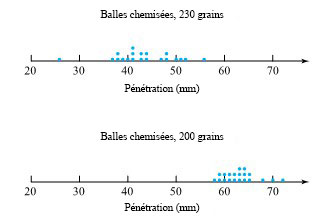
Les diagrammes à points montrent que la pénétration des balles de 200 grains est à la fois plus importante et plus uniforme que celle des balles de 230 grains. (Les étudiant.e.s avaient prédit des pénétrations plus importantes pour les balles plus légères sur la base d’une plus grande vitesse initiale et d’une plus petite surface d’action du frottement. Les différences d’uniformité de la pénétration n’étaient ni prévues ni expliquées.)
Les diagrammes à points donnent une idée générale d’un ensemble de données, mais ils ne permettent pas toujours de récupérer les valeurs utilisées pour les créer. Un diagramme à tiges et à feuilles contient à peu près les mêmes informations visuelles qu’un diagramme à points, tout en préservant exactement les valeurs d’origine. Ce type de diagramme se construit en utilisant les derniers chiffres de chaque point de données pour indiquer où il se situe.

Exemple 2.1.2.1 Représentation du faux-rond des engrenages (suite)
La figure 2.1.2.3 présente deux diagrammes à tiges et à feuilles possibles pour le faux-ronds de la face de poussée des engrenages empilés. Dans les deux cas, le premier chiffre de chaque observation est représenté par le nombre situé à gauche de la ligne verticale (la « tige ») du diagramme. Les nombres situés à droite de la ligne verticale constituent les « feuilles » et donnent le deuxième chiffre des faux-ronds observés. Le deuxième diagramme est un peu plus détaillé que le premier : il indique les positions des feuilles « 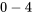 » et «
» et « 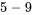 » pour chaque premier chiffre possible, au lieu d’une seule feuille «
» pour chaque premier chiffre possible, au lieu d’une seule feuille « 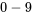 » pour chaque premier chiffre.
» pour chaque premier chiffre.
Exemple 2.1.2.2 Pénétration des balles de 200 grains, suite
La figure 2.1.2.4 présente deux diagrammes à tiges et à feuilles possibles pour la pénétration de balles de 200 grains (données du tableau 2.1.2.1). Sur ces diagrammes, il était pratique d’utiliser les deux chiffres à gauche de la virgule pour la tige et les deux chiffres à droite de la virgule pour les feuilles. Le premier diagramme a été réalisé en consignant les valeurs des feuilles directement à partir du tableau (de gauche à droite et de haut en bas). Le deuxième diagramme est meilleur : on l’a obtenu en ordonnant les valeurs qui composent chaque feuille. À noter que les deux diagrammes donnent essentiellement la même impression visuelle que le deuxième diagramme à points de la figure 2.2.1.2.
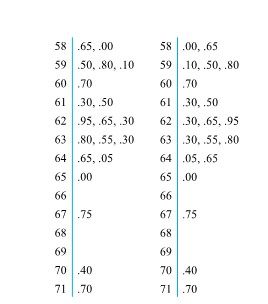
de la profondeur de pénétration de (200 grains)
Pour comparer deux jeux de données, on peut accoler deux diagrammes à tiges et à feuilles.
Exemple 2.1.2.1. Diagrammes accolés des données de faux-rond (suite)