Chapter 5: Trade Restrictions: Non-Tariff Barriers
5.3 The Terms-of-Trade Effect of an Import Quota – The Large-Country Case
As in the case of tariffs, a key question is whether an import quota can benefit a nation economically. We have concluded that an import quota reduces the economic well-being of a small nation. However, if the importing nation has a large enough share of the world market that it is able to influence the price of the imported product, then an import quota can bring economic benefits as the quota can reduce the quantity of imports and, therefore, the sales of foreign suppliers. The reduction of imports pushes foreign suppliers to reduce their product price in an effort to maintain their sales. With import prices falling – relative to export prices, the importing country experiences an improvement in its terms of trade. That is, there is a terms-of-trade effect. If the terms-of-trade effect is large enough to outweigh the negative effects of the usual deadweight losses due to the production and consumption effects, then the large country can gain from an import quota.
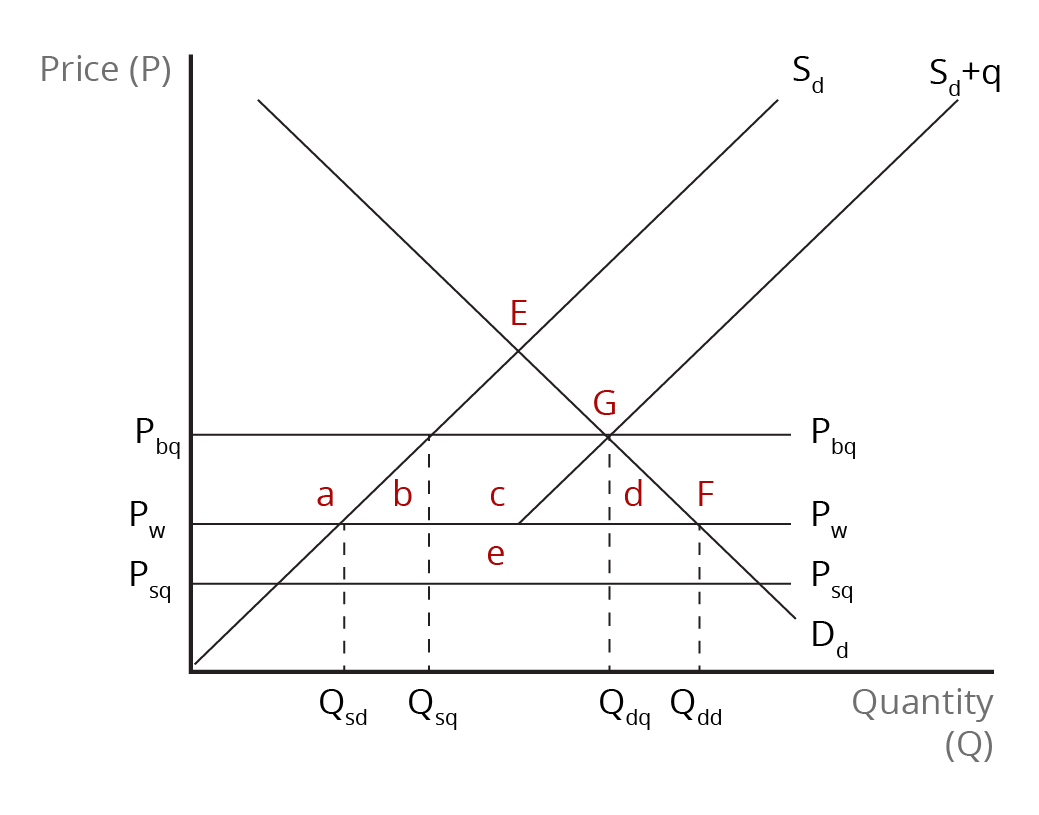
The analysis of the effects of an import quota in the large-country case is shown in Figure 5.2 and Table 5.2. The demand for the imported product is given by [latex]\text{D}_{d}[/latex], and the domestic supply is given by [latex]\text{S}_{d}[/latex]. The intersection of supply and demand in the importing country before trade determines the equilibrium price and quantity at point [latex]\text{E}[/latex]. When the domestic market opens up to international trade, the importing country faces an international price of [latex]\text{P}_{w}[/latex]. With free trade, equilibrium in the domestic markets shifts to point [latex]\text{F}[/latex]. Domestic consumers now purchase [latex]\text{Q}_{dw}[/latex], and domestic producers supply [latex]\text{Q}_{sw}[/latex]. The difference between the quantity purchased and the quantity supplied domestically (i.e., [latex]\text{Q}_{dw}-\text{Q}_{sw}[/latex]) represents the initial quantity of imports prior to the imposition of the quota.
Credit: © by Kenrick H. Jordan and Conestoga College, CC BY-NC-SA 4.0.
Now, suppose the large importing nation imposes an import quota. This changes the supply situation within the domestic market. Below the world price line [latex](\text{P}_{w})[/latex], supply comes only from domestic producers; above the world price line, the domestic supply [latex](\text{S}_{d})[/latex] increases by the extent of the quota (i.e., the quota quantity). The pertinent domestic supply curve with international trade now becomes [latex]\text{S}_{d}+\textit{q}[/latex], where [latex]\textit{q}[/latex] represents the quota quantity. For the quota to be effective, the level of imports must be set below the level which would have occurred in the absence of free trade (i.e., [latex]\text{Q}_{dd}-\text{Q}_{sd}[/latex]).
Since supply is now reduced below the free-trade level, the domestic price rises above the world price and is given by the intersection of the “new” supply curve, [latex]\text{S}_{d}+\textit{q}[/latex], and the demand curve, [latex]\text{D}_{d}[/latex]. The domestic price [latex](\text{P}_{bq})[/latex] is indicated by the horizontal line – parallel to and above the world price, [latex]\text{P}_{w}[/latex]. The market equilibrium now shifts to point [latex]\text{G}[/latex]. With the large importing country able to exercise buying power, the price received by foreign suppliers in the import market [latex](\text{P}_{sq})[/latex] lies parallel to and below the world price.
The increase in the domestic price leads to an increase in domestic production from [latex]\text{Q}_{sd}[/latex] to [latex]\textit{Q}_{sq}[/latex] and a reduction in domestic consumption from [latex]\text{Q}_{dd}[/latex] to [latex]\textit{Q}_{dq}[/latex]. As a result, the quantity of imports falls to the difference between [latex]\textit{Q}_{dq}[/latex] and [latex]\textit{Q}_{sq}[/latex]. In the domestic market, consumer surplus falls by the sum of areas[latex]\textit{a}[/latex], [latex]\textit{b}[/latex], [latex]\textit{c}[/latex], and [latex]\textit{d}[/latex]. Meanwhile, producer surplus increases by area [latex]\textit{a}[/latex], as there is a transfer of economic surplus from consumers to domestic producers. The results of our analysis so far are similar to those in the case of a small importing country. Because the quota leads to a reduction in the export price of the product, the price export suppliers receive, [latex]\text{P}_{sq}[/latex], lies below the world price, [latex]\text{P}_{w}[/latex]. With the quota mark-up being equal to the vertical difference between the price lines [latex]\text{P}_{bq}[/latex] and [latex]\text{P}_{sq}[/latex], the tariff-equivalent revenue (or quota rent) is equal to the quantity of imports [latex](\textit{Q}_{dq}-\textit{Q}_{sq})[/latex] multiplied by the quota mark-up or the sum of area [latex]\textit{c}[/latex] and area [latex]\textit{e}[/latex]. Here, we can see that a portion of the tariff-equivalent revenue, equal to area [latex]\textit{c}[/latex], is collected from domestic consumers while the remainder is contributed by foreign suppliers of the imported product, area [latex]\textit{e}[/latex]. Area [latex]\textit{e}[/latex] represents the terms-of-trade effect, which is a transfer of economic surplus from suppliers in the exporting country to the importing country. A large importing country, therefore, can use an import quota to improve its terms of trade and, consequently, its national well-being.
If we combine the various economic effects of the import quota on consumers, domestic producers, and other national stakeholders (e.g. import distributors and government), we can determine the overall economic impact of the quota on the nation as a whole.
- The losses in consumer surplus of areas [latex]\textit{a}[/latex] and [latex]\textit{c}[/latex] are offset by gains to producers and the part of tariff-equivalent revenue that is obtained from domestic sources.
- The part of the tariff-equivalent revenue that foreigner suppliers pay, area [latex]\textit{e}[/latex], represents a gain for the importing nation.
- The importing nation suffers the usual deadweight losses of area [latex]\textit{b}[/latex] and area [latex]\textit{d}[/latex], the production and consumption effects, respectively. This represents a deterioration in the nation’s well-being due to lower consumption and the switch of some consumption to inefficient domestic production.
Whether the importing country gains or loses economic well-being depends on the relative sizes of areas [latex]\textit{b}[/latex] and [latex]\textit{d}[/latex] and area [latex]\textit{e}[/latex].
- If area [latex]\textit{e}[/latex] is greater than areas [latex]\textit{b}+{d}[/latex], the importing country is better off as a result of the import quota.
- If [latex]\textit{e}[/latex] is less than areas [latex]\textit{b}+{d}[/latex], the importing country is worse off as a result of the import quota.
The lower the price received by foreign suppliers of the import, the larger is area [latex]\textit{e}[/latex] and the more likely the large nation will gain from the quota. Table 5.2 summarizes the economic effects of a tariff for a large country.
| Item | Gain/Loss |
|---|---|
| Producer surplus gain or loss | [latex]+\textit{a}[/latex] |
| Consumer surplus gain or loss | [latex]-\textit{a}-{b}-{c}-{d}[/latex] |
| Tariff-equivalent revenue | [latex]+\textit{c}+{e}[/latex] |
| National economic well-being | [latex]\textit{e}-({b}+{d})[/latex] |
As seen, an import quota can improve its terms of trade and the economic well-being of a large importing nation. However, the quota lowers the large country’s well-being by reducing its consumption of lower-cost imports. Formally, the nation can obtain the highest net gain in economic well-being – net benefit – by maximizing the difference between the terms-of-trade effect and the efficiency loss stemming from the production and consumption effects. That is, a nationally optimal quota maximizes the difference between area [latex]\textit{e}[/latex] and areas [latex]\textit{b}+{d}[/latex] in Figure 5.2.
In the large-country case, even though the importing country can obtain benefit as economic surplus is redistributed from foreign suppliers, a nationally optimal quota is still bad for the world. This is because foreign suppliers lose more than the surplus transferred to the importing nation. Not only do foreign suppliers receive lower prices, they also experience a drop in their exports because of the quota. In addition, the exporting country is likely to retaliate in real-world situations, which would lead to further losses in economic surplus. The import quota causes a loss of world economic well-being and hurts the foreign country.
Review: Effects of Import Quota on a Large Country
Review your understanding of import quotas by watching this video [15:57].
Source: Mike Moore. (2020, July 27). Import quota large country. [Video]. YouTube. https://www.youtube.com/watch?v=v_0bB8ckC5k
Image Descriptions
Figure 5.2: The Economic Effects of an Import Quota in a Large Country
The image is a graph with a vertical axis labelled "Price (P)," and a horizontal axis labelled "Quantity (Q)."
Three horizontal lines extending from the lower half of the y-axis are labelled Pbq, PW, and Psq.
There are two supply curves and one demand curve drawn. The original supply curve, labelled Sd, is upward-sloping from the origin point of the graph. To the right, there is a second supply curve, labelled Sd+q, originating from the PW line.
The demand curve labelled Dd is downward sloping. There is an equilibrium point marked "E" where the original supply curve Sd intersects the demand curve Dd far above Pbq. The intersection of Dd and PW is labelled “F.” The intersection of Sd+q, Dd, and Pbq is labelled “G” and falls between E and F on the demand curve.
Four quantity levels are marked along the horizontal axis, Qsd, Qsq, Qdq, and Qdd, with dotted horizontal lines up to the intersections of the price lines and supply curves with the demand curve.
Area a is above the intersection of Sd and PW and below Pq. Area b is the triangle formed by Sd, PW and Qsq. Area c is the rectangle in the middle formed by Qsq, PW, Qdq and Pq, with Sd+q passing through it. Area d mirrors b, formed by Qsq, PW, and Dd. Below the area c, area e is a rectangle formed by Qsq, Psq, Qdq, and PW.
[back]
the tariff revenue that the importing country gets from foreign suppliers of the imported product in the form of lower supply prices
import quota that maximizes the positive difference between the gain due to the improvement in the terms of trade and the loss due to the reduction in imports

