7.4 Newton’s Second Law of Motion

Force, Acceleration, and Velocity

Newton’s Second Law of Motion describes a change in motion, but how exactly does that occur? Well, in order for an object to move, a force needs to act upon it. For the object to continuously move, it either needs to have that force acting upon it to be present continuously and/or for momentum to be gained. How that happens is through acceleration.

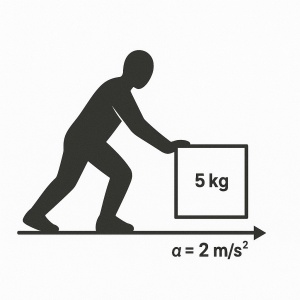
A 5 kg box is pushed across a floor with an acceleration of 2 m/s². What is the force applied to the box using the equation F = ma?

Solution:

[latex]F = 5 \, \text{kg} \times 2 \, \text{m/s}^2[/latex]
[latex]F = 10 \, \text{N}[/latex]

A force of 10 newtons is applied to the box. 

Acceleration can be defined as the rate at which an object changes velocity, or simply, how fast or slow an object speeds up or slows down. This differs from velocity, which describes the rate at which an object is moving over time.

Movement in Action

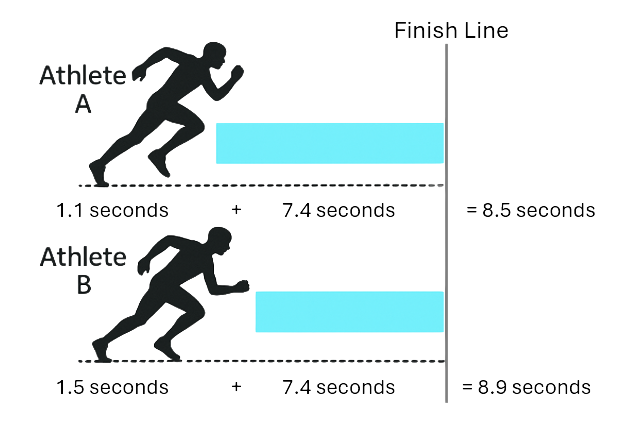
Olympic sprinters train year-round to be the fastest people on the planet. However, their velocity (or speed) is not the only thing that matters. Imagine a 100m race with only two athletes. Both athletes have a top speed of 42 km/h, but one athlete reaches the finish line before the other. Why is that? You may want to consider acceleration. How quickly was each athlete able to reach their top speed and maintain it?

Consider the athletes above. Both athletes run at the top speed for 7.4 seconds; however, Athlete A only take 1.1 seconds to reach that top speed, whereas Athlete B takes 1.5 seconds (0.4 seconds longer). As a result, Athlete A finished 0.4 seconds before Athlete B.

Calculating Acceleration

When calculating acceleration, consider what information you have and choose one of the following two options:

Using Force and Mass

If you know the force applied and the mass of the object, you can calculate the acceleration:

[latex]a = \frac{F}{m}[/latex]

• a = acceleration (m/s²)
• F = force (N)
• m = mass (kg)

Using Force and Mass to Calculate Acceleration

 

 

A force of 20 N is applied to a shopping cart with a mass of 4 kg. What is the acceleration of the cart using the equation [latex]a = \frac{F}{m}[/latex]?

Solution:

[latex]a = \frac{20 \, \text{N}}{4 \, \text{kg}}[/latex]
[latex]a = 5 \, \text{m/s}^2[/latex]

The acceleration of the shopping cart is 5 meters per second squared (5 m/s²).

 

Using Change in Velocity and Time

If you know the initial and final velocity and the time over which the change happens, you can calculate the acceleration:

[latex]a = \frac{\Delta v}{\Delta t}[/latex]

• a = acceleration (m/s²)
• ∆v = change in velocity (final velocity – initial velocity)
• ∆t = change in time (time interval over which the change occurs)

Using Change and Velocity to Calculate Acceleration

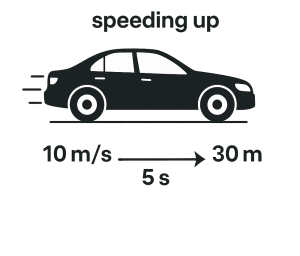
A car speeds up from 10 m/s to 30 m/s in 5 seconds. What is the acceleration using the formula [latex]a = \frac{F}{m}[/latex]?

Solution:

Initial velocity ([latex]v_i[/latex]) = 10 m/s
Final velocity ([latex]v_f[/latex]) = 30 m/s
Time ([latex]{\Delta t}[/latex]) = 5 s

Plug into the formula here

[latex]a = \frac{v_f - v_i}{\Delta t} = \frac{30 \, \text{m/s} - 10 \, \text{m/s}}{5 \, \text{s}} = \frac{20 \, \text{m/s}}{5 \, \text{s}} = 4 \, \text{m/s}^2[/latex]

The car’s acceleration is 4 m/s².

 

 

Momentum vs Acceleration

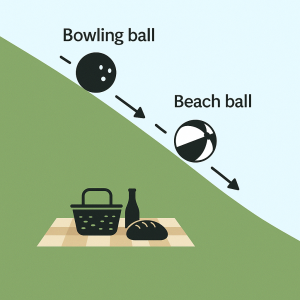
Like acceleration, momentum involves motion of an object; however, what contributes to momentum differs. As previously noted, acceleration is a product of force and mass (or of Δv ÷ Δt), while momentum is a product of mass and velocity. This means that if an object is moving, it has momentum that is proportionally equivalent to its mass and its current velocity.

Imagine a beach ball and a bowling ball rolling down a slight hill. They are both rolling toward you at the same velocity (or speed), and you have to stop them both from rolling into your picnic lunch. Which one are you more concerned about? Likely not the beach ball because while it is coming toward you as fast as the bowling ball, it has only a small amount of mass and therefore a small amount of momentum. The bowling ball, however, has much more mass and therefore much more momentum.

To calculate momentum (p), consider the following:

[latex]p = mv[/latex]

• p = momentum (in kilogram meters per second, kg·m/s)
• m = mass (in kilograms, kg)
• v = velocity (in meters per second, m/s)

Calculating Momentum

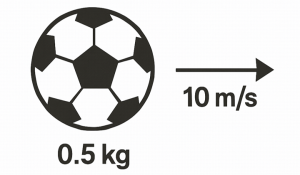
A soccer ball has a mass of 0.5 kg and is moving at a velocity of 10 m/s. What is its momentum using the formula [latex]p=mv[/latex]?

Solution:

[latex]p = 0.5 \, \text{kg} \times 10 \, \text{m/s}[/latex]
[latex]p = 5 \, \text{kg} \cdot \text{m/s}[/latex]

The momentum of the soccer ball is 5 kg m/s.

“Force and Acceleration” image: OpenAI. (2025). ChatGPT. [Large language model]. https://chat.openai.com/chat  Prompt: A 5 kg box being pushed across a floor with an acceleration of 2 m/s².

“100m dash” image: OpenAI. (2025). ChatGPT. [Large language model]. https://chat.openai.com/chat  Prompt: Using the image provided, draw two athletes in a race, comparing how long it took them to accelerate to their top speed and how that changes the race outcome.

“Shopping cart” image: OpenAI. (2025). ChatGPT. [Large language model]. https://chat.openai.com/chat  Prompt: Create an image of a shopping cart that has a mass of 4kg being pushed with a force of 20 N.

“Speeding car” image: OpenAI. (2025). ChatGPT. [Large language model]. https://chat.openai.com/chat  Prompt: Create an illustration of a car speeding up from 10 m/s to 30 m/s in 5 seconds.

“Momentum” image: OpenAI. (2025). ChatGPT. [Large language model]. https://chat.openai.com/chat  Prompt: Image of a bowling bowl and beach bowl rolling down a hill with a picnic lunch at the bottom.

“Soccer ball” image: OpenAI. (2025). ChatGPT. [Large language model]. https://chat.openai.com/chat  Prompt: A soccer ball that has a mass of 0.5 kg and is moving at a velocity of 10 m/s.