3 Propriétés d’ordre
Ordre sur ![]() . Pour tout nombres réels
. Pour tout nombres réels ![]() et
et ![]() , on a soit
, on a soit
![]()
On dénote
![]()
On a
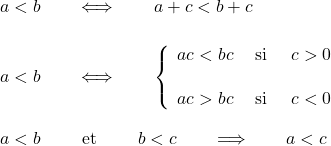
Exercice 1
Exercice 2
Exercice 3
Exercice 4
Ordre sur ![]() . Pour tout nombres réels
. Pour tout nombres réels ![]() et
et ![]() , on a soit
, on a soit
![]()
On dénote
![]()
On a
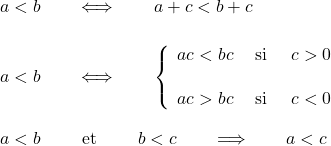
Exercice 1
Exercice 2
Exercice 3
Exercice 4