19 Inéquations Linéaires
![]() Une inégalité linéaire est une expression de la forme
Une inégalité linéaire est une expression de la forme ![]() , ou
, ou ![]() , ou
, ou ![]() , ou bien
, ou bien ![]() , où
, où ![]() est une variable.
est une variable.
La variable qui vérifie l’inégalité est dite solution de l’équation.
![]() Comment résoudre , par exemple,
Comment résoudre , par exemple, ![]() ?
?
– regrouper tous les termes variables d’un côté
– regrouper tous les termes constants de l’autre côté
– diviser chacun des côté par le coefficient de la variable et changer les inégalités à ![]() si
si ![]() .
.
![]()
![]()
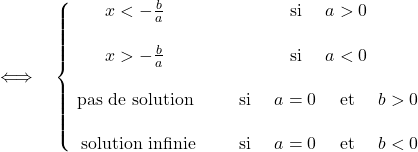
Exercice 1
Afficher/Masquer Solution.
L’ensemble des solutions est l’intervalle : ![]() .
.
Exercice 2
Afficher/Masquer Solution.
L’ensemble des solutions est l’intervalle : ![]() .
.
Exercice 3
Afficher/Masquer Solution.
On a
![]()
![]()
![]()
ce qui est faux pour tout ![]() car
car ![]()
![]() .
.
L’ensemble des solutions est l’intervalle : ![]() .
.

