29 Graphes
Courbe plane : C’est le graphe d’une équation à deux variables; l’ensemble de tous les points ![]() qui satisfont l’équation.
qui satisfont l’équation.
En particulier, le graphe d’une fonction ![]() est l’ensemble
est l’ensemble
![]()
- abscisse à l’origine = l’abscisse
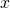 d’un point où le graphe rencontre l’axe des abscisses
d’un point où le graphe rencontre l’axe des abscisses 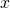 .
. - ordonnée à l’origine = l’ordonnée
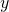 d’un point où le graphe rencontre l’axe des ordonnées
d’un point où le graphe rencontre l’axe des ordonnées 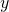 .
.
Symétrie : un graphe ![]() est
est
– symétrique par rapport à l’axe des ![]() si :
si : ![]()
– symétrique par rapport à l’axe des ![]() si :
si : ![]()
– symétrique par rapport à l’origine si : ![]()
– symétrique par rapport à la droite ![]() si :
si : ![]()
Exercice 1
Show/Hide Solution.
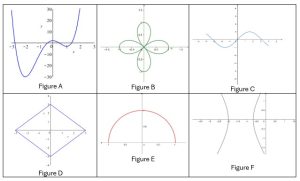
Figure A est le graphe d’une fonction car la règle de la droite verticale est satisfaite.
Figure B n’est pas le graphe d’une fonction car la règle de la droite verticale n’est pas satisfaite.
Figure C est le graphe d’une fonction car la règle de la droite verticale est satisfaite.
Figure D ne peut être le graphe d’une fonction car la droite verticale ![]() rencontre la courbe en deux points distincts
rencontre la courbe en deux points distincts ![]() et
et ![]() .
.
Figure E est le graphe d’une fonction car la règle de la droite verticale est satisfaite.
Figure F n’est pas le graphe d’une fonction car la règle de la droite verticale n’est pas satisfaite.
Exercice 2
Show/Hide Solution.
Posons ![]() , alors
, alors ![]() . Donc
. Donc ![]() sont les ordonnées à l’origine.
sont les ordonnées à l’origine.
Posons ![]() , alors
, alors ![]() . Donc
. Donc ![]() sont les abscisses à l’origine.
sont les abscisses à l’origine.
nbsp;
Exercice 3
Show/Hide Solution.
Posons ![]() , alors
, alors ![]() . Donc
. Donc ![]() sont les abscisses à l’origine.
sont les abscisses à l’origine.
Posons ![]() , alors
, alors ![]() . Donc
. Donc ![]() est l’ordonnée à l’origine.
est l’ordonnée à l’origine.
nbsp;
Exercice 4
Show/Hide Solution.
* Substituer ![]() pour
pour ![]() :
: ![]() .
.
Comme l’équation n’a pas changé, le graphe a une symétrie par rapport à l’axe des ![]() .
.
* Substituer ![]() pour
pour ![]() :
: ![]() .
.
Comme l’équation n’a pas changé, le graphe a une symétrie par rapport à l’axe des ![]() .
.
* Substituer ![]() pour
pour ![]() et
et ![]() pour
pour ![]() :
: ![]() .
.
Comme l’équation n’a pas changé, le graphe a une symétrie par rapport l’origine.
nbsp;
Exercice 5
Show/Hide Solution.
* Substituer ![]() pour
pour ![]() :
: ![]() .
.
Comme l’équation a changé, le graphe n’a pas de symétrie par rapport à l’axe des ![]() .
.
* Substituer ![]() pour
pour ![]() :
: ![]() .
.
Comme l’équation a changé, le graphe n’a pas de symétrie par rapport à l’axe des ![]() .
.
* Substituer ![]() pour
pour ![]() et
et ![]() pour
pour ![]() :
: ![]() .
.
Comme l’équation a changé, le graphe n’a pas de symétrie par rapport à l’origine.

