10 Exposants entiers
facteurs de 
pour tout différent de zéro
est indéfini
est indéfini pour tout entier positif.
Lois des exposants
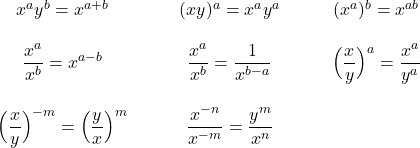
Exercice 1
Afficher/Masquer Solution.
En utilisant les lois des exposants, on a
![\[ \displaystyle{ \frac{a^{{-5}} \Big( {-2} a^{{-2}} \Big)^{{4}} }{ a^{{3}} } = ({-2})^{{4}} a^{({-2}).({4} ) +( {-5}) -({3}) } = {16} a^{{-16}} }.\]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-6cc68c5bc4afdfe79069880b796cb2c4_l3.png "Rendered by QuickLaTeX.com")
Exercice 2
Afficher/Masquer Solution.
En utilisant les lois des exposants, on a
![\[ \displaystyle{ \frac{ ( x^{{-4}} y^{{5}} )^4 ( x^{{-4}} y^{{5}} )^{-3} } { x^{{-7}} y^{{8}} } = \frac{ x^{4({-4}) + (-3)({-4})} . y^{4({5}) + (-3)({5}) } }{ x^{{-7}} y^{{8}} } = \frac{ x^{{-4}} y^{{5}} } { x^{{-7}} y^{{8}} } =\frac{ x^{{-4} -( {-7})} } { y^{{8} - {5}} } = \frac{ x^{{3}} } { y^{{3}} } } .\]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-be0a757211567553a9ff32233bb11413_l3.png "Rendered by QuickLaTeX.com")
Exercice 3
Afficher/Masquer Solution.
En utilisant les lois des exposants, on a
![\[ \displaystyle{ \Big( \frac{ y^{{3}} x^{{-6}} }{ y^{{4}} x^{{-5}} }\Big) \Big(\frac{ x^{{-7}} }{ y^{{-2}} } \Big)^{3} =\frac{ y^{{3} - ({4}) -3({-2}) } } { x^{{-5}-({-6}) -3({-7}) } } = \frac{ y^{{5}} } { x^{{22}} } } .\]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-8e7a2c9f8d4508c1f19b7201c9e947fd_l3.png "Rendered by QuickLaTeX.com")
Exercice 4
Afficher/Masquer Solution.
En utilisant les lois des exposants, on a
![\[ \Big( {6} x^{{3}} y^{{6}} \Big)\Big( \frac{1}{{3}} y^{{4}} \Big) = \frac{{6}}{ {3}} x^{{3}}y^{({6})+({4}) } ={2} x^{{3}} y^{{10}} .\]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-8dfb94182299b803134181158c34fb95_l3.png "Rendered by QuickLaTeX.com")
