4 Union, Intersection et Intervalles
Un ensemble est une collection d’objets bien définis, appelés éléments.
Si 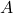 est un ensemble et
est un ensemble et  un élément de
un élément de 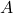 , on note
, on note 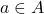 .
.
Si ![]() n’est pas un élément de
n’est pas un élément de ![]() , on note
, on note ![]() .
.
L’ensemble vide, noté, 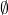 , ne contient aucun élément.
, ne contient aucun élément.
Un ensemble 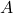 est un sous ensemble de l’ensemble
est un sous ensemble de l’ensemble 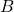 si chaque élément de
si chaque élément de 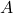 est un élément de
est un élément de 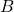 et on note
et on note 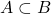 .
.

![Rendered by QuickLaTeX.com \begin{matrix} (a,b)= \{ x : \quad a< x< b\} \qquad \qquad \qquad (a,+\infty)= \{ x : \quad a< x\}\\ \\ [a,b]= \{ x : \quad a \leqslant x\leqslant b\}\qquad \qquad \qquad [a,+\infty)= \{ x : \quad a \leqslant x\} \\ \\ [a,b)= \{ x :\quad a \leqslant x< b\} \qquad \qquad \qquad (-\infty,b)= \{ x : \quad x< b\}\\ \\ (a,b]= \{ x :\quad a<x \leqslant b\} \qquad \qquad \qquad (-\infty,b] = \{ x : \quad x \leqslant b\}\\ \\ (-\infty,+\infty)= \mathbb{R}\qquad \qquad \hbox{ ensemble des nombres reels } \end{matrix}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-c11e5df6b811775ddc0bbf29600e8b70_l3.png)
Exercice 1
Exercice 2
Exercice 3
Exercice 4
Exercice 4

