2 Addition et multiplication de réels
![]() Deux opérations, addition et multiplication, sont définies sur
Deux opérations, addition et multiplication, sont définies sur ![]() et satisfont les lois de
et satisfont les lois de

![]() Les propriétés suivantes sont vraies pour tout
Les propriétés suivantes sont vraies pour tout ![]()
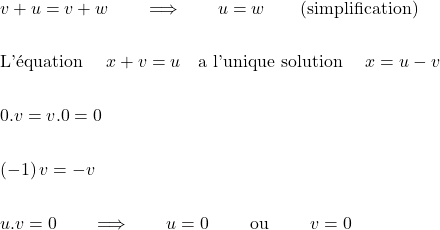
![]() L’opération de soustraction est définie par :
L’opération de soustraction est définie par : ![]()
![]() L’opération de division est définie par :
L’opération de division est définie par : ![]() et satisfait
et satisfait
![]()
![]()
Exercice 1
Afficher/Masquer Solution.
i) ![]() On a
On a
![]()
![]()
ii) ![]() On a
On a
![]()
iii) ![]() On a
On a
![]()
Exercice 2
Afficher/Masquer Solution.
i) ![]() Contre-exemple:
Contre-exemple:
![]() et
et ![]() , mais
, mais ![]() .
.
![]() , mais
, mais ![]() .
.
ii) ![]() Contre-exemple:
Contre-exemple:
![]() mais
mais ![]() .
.
iii) ![]() Soient
Soient![]() et
et ![]() . On a
. On a
![]() avec
avec ![]() et
et ![]() .
.
Alors
![]()
car ![]() et
et ![]() avec
avec ![]() .
.
Exercice 3
Afficher/Masquer Solution.
i) ![]() On a
On a
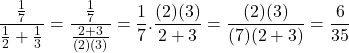 .
.
ii) ![]() On a
On a
![]() .
.
iii) ![]() On a
On a
![]()

