30 Parabole
Une fonction quadratique ![]() peut s’exprimer sous la forme standard
peut s’exprimer sous la forme standard
![]()
en complétant le carré parfait.
Le graphe de ![]() est une parabole de sommet
est une parabole de sommet ![]() .
.
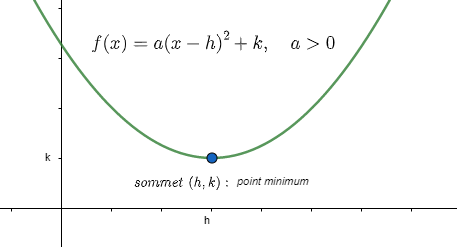
![]() Si
Si ![]() , alors
, alors
– la parabole s’ouvre vers le haut et
– la valeur minimale de ![]() est
est ![]()
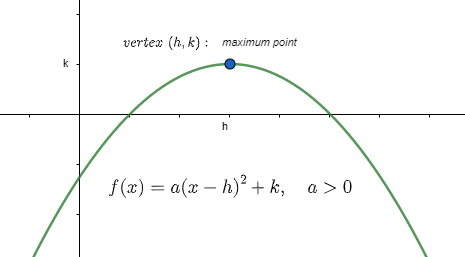
![]() Si
Si ![]() , alors
, alors
– la parabole s’ouvre vers le bas et
– la valeur maximale de ![]() est
est ![]()
Exercice 1
Show/Hide Solution.
L’équation de la fonction quadratique, dans sa forme standard, est :
![]()
![]()
Donc,
– le sommet est : ![]()
– la valeur maximale est : ![]() .
.
Poser ![]() , alors
, alors ![]() . Donc , il n’y a pas d’ abscisses à l’origine.
. Donc , il n’y a pas d’ abscisses à l’origine.
Poser ![]() , alors
, alors ![]() . Donc
. Donc ![]() est l’ordonnée à l’origine.
est l’ordonnée à l’origine.
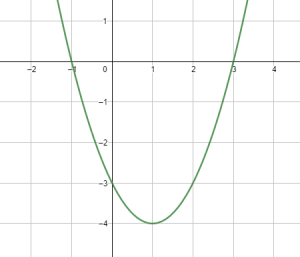
Exercice 2
Show/Hide Solution.
Poser ![]() . Alors
. Alors ![]() . Donc,
. Donc, ![]() ou
ou ![]() sont les abscisses à l’origine.
sont les abscisses à l’origine.
Poser ![]() . Alors
. Alors ![]() . Donc,
. Donc, ![]() est l’ordonnée à l’origine.
est l’ordonnée à l’origine.
L’équation de la fonction quadratique, sous sa forme standard, est :
![]()
Donc,
– le sommet est : ![]()
– la valeur minimale est : -{4}.

