25 Cercles
Un cercle de centre ![]() et de rayon
et de rayon ![]() est l’ensemble des points
est l’ensemble des points ![]() dans le plan
dans le plan ![]() qui sont situés à la distance
qui sont situés à la distance ![]() de
de ![]() .
.
L’équation du cercle est obtenue par :
![]()
Le cercle unité est le cercle de centre ![]() et de rayon 1, décrit par l’équation:
et de rayon 1, décrit par l’équation: ![]() .
.
Exercice 1
Afficher/Masquer Solution.
Le rayon est égale à la longueur du segment de droite joignant le centre et le point de rencontre ![]() avec l’axe des
avec l’axe des ![]() .
.
En utilisant la formule de la distance, on obtient
![]()
L’équation du cercle est donnée par :
![]()
Exercice 2
Afficher/Masquer Solution.
En complétant les carrés parfaits, on obtient:
![]()
![]()
Le centre est point ![]() et le rayon est
et le rayon est ![]() .
.
Exercice 3
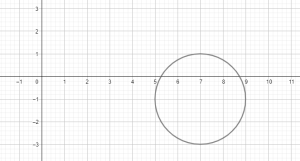
Afficher/Masquer Solution.
Les coordonnées du centre sont ![]() .
.
L’équation du cercle est donnée par :
![]()
ou bien ![]() .
.

