24 Droites
La pente ![]() d’une droite non verticale passant par les points
d’une droite non verticale passant par les points ![]() et
et ![]() est
est
![]()
![]() L’équation d’une droite passant par le point
L’équation d’une droite passant par le point ![]() et de pente
et de pente ![]() est
est
![]()
Si ![]() alors
alors
![]()
![]()
![]() Une droite horizontale (pente 0) est perpendiculaire a une droite verticale (pente non définie)
Une droite horizontale (pente 0) est perpendiculaire a une droite verticale (pente non définie)
Exercice 1
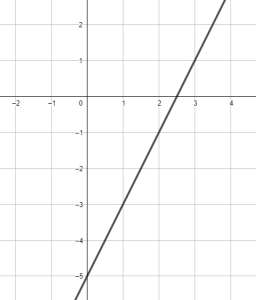
Afficher/Masquer Solution.
La droite passe par les points ![]() et
et ![]() .
.
L’équation générale de cette droite est de la forme : ![]()
Pour ![]() , on a
, on a ![]() .
.
Pour ![]() , on obtient
, on obtient ![]() .
.
Donc ![]() et
et ![]() .
.
L’équation de la droite est : ![]() .
.
Exercice 2
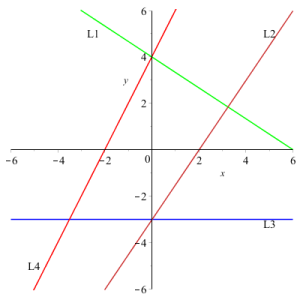
Afficher/Masquer Solution.
La droite ![]() passe par les points
passe par les points ![]() et
et ![]() . Son équation est :
. Son équation est : ![]() .
.
La droite ![]() est horizontale et passe par le point
est horizontale et passe par le point ![]() . Sa pente est nulle et son équation est :
. Sa pente est nulle et son équation est : ![]() .
.
La droite ![]() passe par les points
passe par les points ![]() et
et ![]() . Donc, son équation est :
. Donc, son équation est : ![]() .
.
Finalement, l’équation de la droite ![]() est :
est : ![]() .
.
Exercice 3
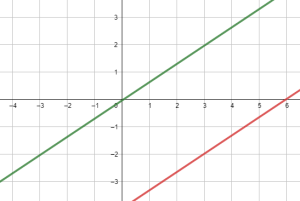
Afficher/Masquer Solution.
L’équation de la droite passant par les points ![]() et
et ![]() est donnée par
est donnée par
![]()
L’équation de la droite passant par les points ![]() et
et ![]() est donnée par
est donnée par
![]()
Les deux droites sont parallèles car elles ont la même pente ![]() .
.
Exercice 4
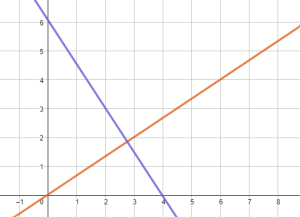
Afficher/Masquer Solution.
L’équation de la droite passant par les points ![]() et
et ![]() est donnée par
est donnée par
![]()
L’équation de la droite passant par les points![]() et
et ![]() est donnée par
est donnée par
![]()
Les deux droites sont perpendiculaires car leurs pentes sont inverses et de signes contraires : ![]() .
.

