23 Coordonnées et Distance
- Soit O un point fixe dans le plan, appelé l’origine.
- Deux droites perpendiculaires passant par O sont appelées axes de coordonnées et notées axe des
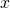 , et axe des
, et axe des 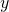 .
.
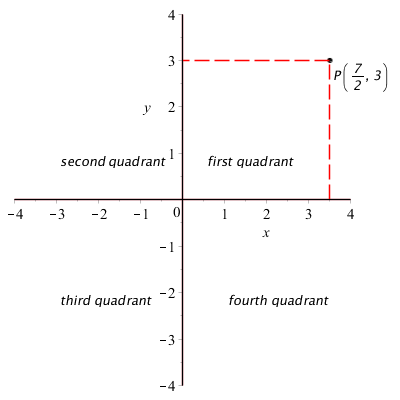
- Les axes divisent le plan en 4 parties, appelées
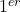 ,
, 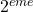 ,
, 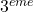 et
et 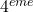 quadrant.
quadrant.
- Un point
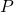 du plan est représenté par le couple ordonné
du plan est représenté par le couple ordonné 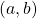 de nombres réels
de nombres réels  et
et 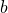 , appelés coordonnées de
, appelés coordonnées de 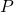 .
.  est la coordonnée des abscisses
est la coordonnée des abscisses 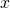 ,
, 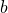 est la coordonnée des ordonnées
est la coordonnée des ordonnées 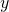 .
.
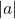 est la distance de
est la distance de 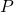 à l’axe des
à l’axe des 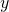 ,
, 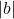 est la distance de
est la distance de 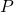 à l’axe des
à l’axe des 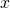 .
.
- La distance entre deux points
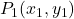 et
et 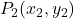 est donnée par:
est donnée par: 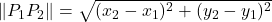 .
.
- Les coordonnées du point milieu du segment de droite joignant
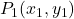 et
et 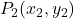 sont données par:
sont données par: 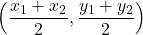
Exercice 1
Exercice 2
Afficher/Masquer Solution.
Les coordonnées du milieu du segment joignant les deux points ![]() et
et ![]() sont
sont
![]()
Exercice 3
Afficher/Masquer Solution.
La longueur des côtés du triangle ![]() sont:
sont:
![]()
![]()
![]()
On a ![]() .
.
Alors, d’après le théorème de Pythagore, ![]() est un triangle droit en
est un triangle droit en ![]() .
.
Exercice 4
Afficher/Masquer Solution.
La distance entre le point ![]() et l’origine est donnée par
et l’origine est donnée par
![]()
La distance entre le point ![]() et l’origine est donnée par
et l’origine est donnée par
![]()
Donc, les points ![]() et
et ![]() sont à la même distance que l’origine.
sont à la même distance que l’origine.
Exercice 5
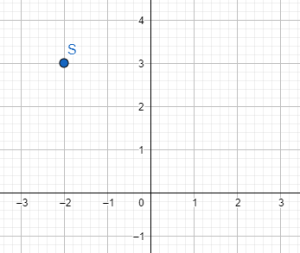
Afficher/Masquer Solution.
La distance du point ![]() à l’axe des
à l’axe des ![]() est
est
![]()
La distance du point ![]() à l’axe des
à l’axe des ![]() est
est
![]()

