14 Simplifier des Expressions Rationnelles
* Une expression rationnelle est une expression qui peut être simplifiée sous la forme 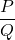 où
où 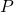 et
et 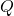 sont des polynômes.
sont des polynômes.
* Pour simplifier une expression rationnelle, on :
– regroupe les numérateurs et les dénominateurs en un quotient simple, puis on divise:
![Rendered by QuickLaTeX.com \[\displaystyle{ \frac{\frac{P}{Q}}{\frac{S}{T}} = \frac{P}{Q} . \frac{T}{S}} \]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-aba83a37ec3924742fd1181500adda0b_l3.png)
– réduit au même dénominateur : 
– réduit en termes d’ordre inférieure : 
Exercice 1
Afficher/Masquer Solution.
On a
![]()
![]()
En simplifiant le facteur commun ![]() , on obtient
, on obtient
![]() .
.
Exercice 2
Afficher/Masquer Solution.
On a
![]() =
= ![]() =
= ![]() .
.
Exercice 3
Afficher/Masquer Solution.
On a
![]()
![]()
En simplifiant le facteur commun ![]() , on obtient
, on obtient
![]() .
.

