8 Multiplication de Polynômes

Multiplication. Le produit de deux polynômes est obtenu en utilisant la propriété de distributivité et la loi des exposants: $x^a x^b = x^{a+b}$ .

Quelques identités remarquables.

$\begin{eqnarray*} && \hbox{différence de deux carrés} \qquad \qquad (a+ b) (a-b) = a^2 - b^2 \\ \\ && \hbox{carré d'une somme} \qquad \qquad (a+b)^2 = a^2 + 2 a b + b^2 \\ \\ && \hbox{carré d'une différence } \qquad (a-b)^2 = a^2 - 2 a b + b^2 \\ \\ && \hbox{cube d'une somme } \qquad \qquad (a+b)^3 = (a+b) (a+b)^2 = a^3 + 3 a^2 b + 3 a b^2 + b^3 \\ \\ &&\hbox{cube d'une différence } \qquad \qquad (a-b)^3 = (a-b) (a-b)^2 = a^3 - 3 a^2 b + 3 a b^2 - b^3 \\ \\ &&\hbox{somme de deux cubes}\qquad\qquad a^3 +b^3 = (a+b) (a^2 - ab + b^2) \\ \\ && \hbox{différence de deux cubes}\qquad \qquad a^3 - b^3 = (a-b) (a^2 + ab + b^2) \end{eqnarray*}$

Voir la Vidéo

Voir sur YouTube

Afficher les Exemples

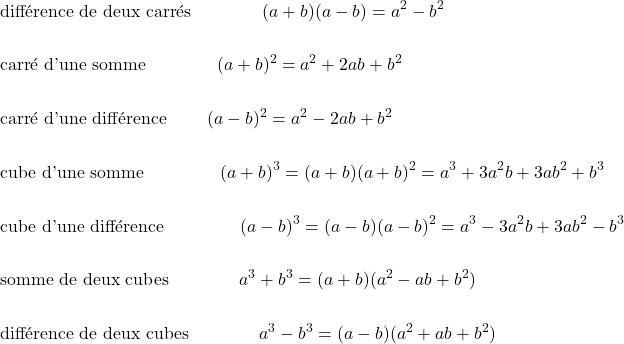
Exercice 1

Afficher/Masquer Solution.

$-2 ( 2 - {5} x ) (- {3} x - 1) + {5} x^2 - {9}$

$= -2( -2 ({3}) x -2 + ({5})({3}) x^2 + {5} x ) + {5} x^2 - {9}$

$= [-2 ({5})({3}) + {5}] x^2 + [4 ({3}) -2({5}) ] x + 4 -{9}$

$= ( {-25}) x^2 +({2})x +({-5})$ .

Exercice 2

Afficher/Masquer Solution.

$(3 t - 1) ( 4 t^2 - 8 t + 3)$

$= (3t) ( 4t^2) - (3t) (8t) + (3t) (3) - 4 t^2 +8 t - 3$

$= 12 t^3 - 28 t^2 + 17 t -3$ .

Exercice 3

Afficher/Masquer Solution.

$4 (-2 t) (1-t^2 )^3 = -8t (1-t^2) (1-t^2)^2$

$=( -8t + 8t^3) ( 1 -2 t^2 + t^4)$

$=-8 t + 16 t^3 - 8 t^5 + 8 t^3 - 16 t^5 + 8 t^7$

$= -8t + 24 t^3 - 24 t^5 + 8 t^7$ .

Exercice 4

Afficher/Masquer Solution.

$(1+t)^4 = (1+t)^2 (1+t)^2 = (1+ 2 t + t^2) (1+2 t + t^2)$

$=$ $1+2 t + t^2 + 2t + 4 t^2 + 2 t^3 + t^2 + 2 t^3 + t^4$

$=$ $1 + 4t + 6 t^2 + 4 t^3 + t^4$ .

Exercice 5

Afficher/Masquer Solution.

$(t + a)^3 = (t + a) (t + a)^2 = (t + a) ( t^2 + 2 at + a^2) = t^3 + 3 a t^2 + 3 a^2 t + a^3$

$(t - a)^3 = (t - a) (t - a)^2 = (t - a) ( t^2 - 2 at + a^2) = t^3 - 3 a t^2 + 3 a^2 t - a^3$

$(t + a)^3 - (t - a)^3= 6 a t^2 + 2 a^3$ .

Exercice 6

Afficher/Masquer Solution.

$(r- s + t ) ( r- s - t)$

$= r^2 - r s - r t - s r + s^2 + s t + t r - t s - t^2$

$= r^2 + s^2 - t^2 - 2 rs$ .

Licence

Symbole de Licence Creative Commons Attribution - Pas d’utilisation commerciale - Pas de modification 4.0 International

Guide de Révision du Pré-calcul Droit d'auteur © 2025 par Samia CHALLAL est sous licence Licence Creative Commons Attribution - Pas d’utilisation commerciale - Pas de modification 4.0 International, sauf indication contraire.

Partagez ce livre