CVP and Breakeven Analyses
6.5 CVP Analysis Using a Financial Calculator
In this section, we'll explore how to use the Texas Instruments BA II Plus financial calculator for conducting break-even and Cost-Volume-Profit (CVP) analyses. We will specifically look at the break-even worksheet, a useful feature for these types of analyses.
The break-even worksheet on the BA II Plus, shown in Figure 6.5.1, can be accessed by using the secondary function of the "6" key. To do this, press the "2ND" key followed by "6". This worksheet includes five variables: Fixed Costs, Variable Costs per Unit, Selling Price, Net Income, and Quantity.
When using the calculator's worksheet:
- FC represents the fixed costs.
- VC represents the variable costs per unit.
- P represents the selling price per unit in the calculator, which differs from the algebraic SP notation.
- PFT stands for profit and denotes the net income in the calculator, which contrasts with the algebraic NI for net income.
- Q represents quantity, volume, or the number of units in the calculator, instead of the algebraic x notation.
Understanding how these variables align with the algebraic approach and how to input them into the calculator is crucial for accurate break-even and CVP analysis.

Figure 6.5.1: The Break-Even Woksheet and its variables
How to use the Break-Even Worksheet
1. Activate the Break-Even Worksheet by pressing the "2ND" function key followed by "6".
2. Clear the worksheet (reset all variables to zero) by pressing the "2ND" function key followed by the "CE|C" key.
3. Press the up and down arrows to access the different variables.
4. Input the known values to their corresponding variables and then press "ENTER".
5. Navigate to the variable you want to compute and press the "CPT" (compute) button to get the result.
A company sells webcams for $85 each. Its fixed costs are $18,500 per month, and the variable costs per unit are $35. a) Calculate the number of webcams the company needs to sell each month to break even. b) Calculate the break-even in dollars.
Watch Video
Show/Hide Solution
The selling price is $85, so [asciimath]SP=$85[/asciimath]
The variable costs per webcam are $35, so [asciimath]VC=$35[/asciimath]
The fixed costs are $18,500, so [asciimath]FC=$18,500[/asciimath]
a) To find the quantity at break-even, we input the given values in the break-even worksheet to their corresponding variables and then compute Q (quantity). Note that at breakeven, net income is zero, so we enter zero for PFT:

Therefore, the company needs to sell 370 webcams each month to break even.
b) Break-eve in dollars is the total revenue at break-even quantity ([asciimath]X_B=370[/asciimath]).
[asciimath]TR=SP.X[/asciimath]
[asciimath]TR=85*X[/asciimath]
[asciimath]TR_B=85(370)[/asciimath]
[asciimath]=$31,450[/asciimath]
Vida runs a business that makes custom-printed shirts. She must make 84 T-shirts each month to break even. It will cost her $5 to purchase and $2 to print each T-shirt. She will have to pay a rent of $1,596 per month for her workshop. a) What is the selling price per T-shirt to break even? b) What is the total revenue needed to break even? C) In February, she sold 60 T-shirts. Did she make a profit or incur a loss and by how much?
Show/Hide Solution
The number of T-shirts at the break-even point is 84, so quantity [asciimath]Q=84[/asciimath]
The variable cost per T-shirt is the sum of the cost of purchasing and printing, so [asciimath]VC=$5+$2=$7[/asciimath]
The only fixed cost is the workshop rent, so [asciimath]FC=$1596[/asciimath]
a) To find the selling price (P) at break-even, we input the given values in the break-even worksheet to their corresponding variables and then compute P. Note that at break-even, net income is zero, so we enter zero for PFT:
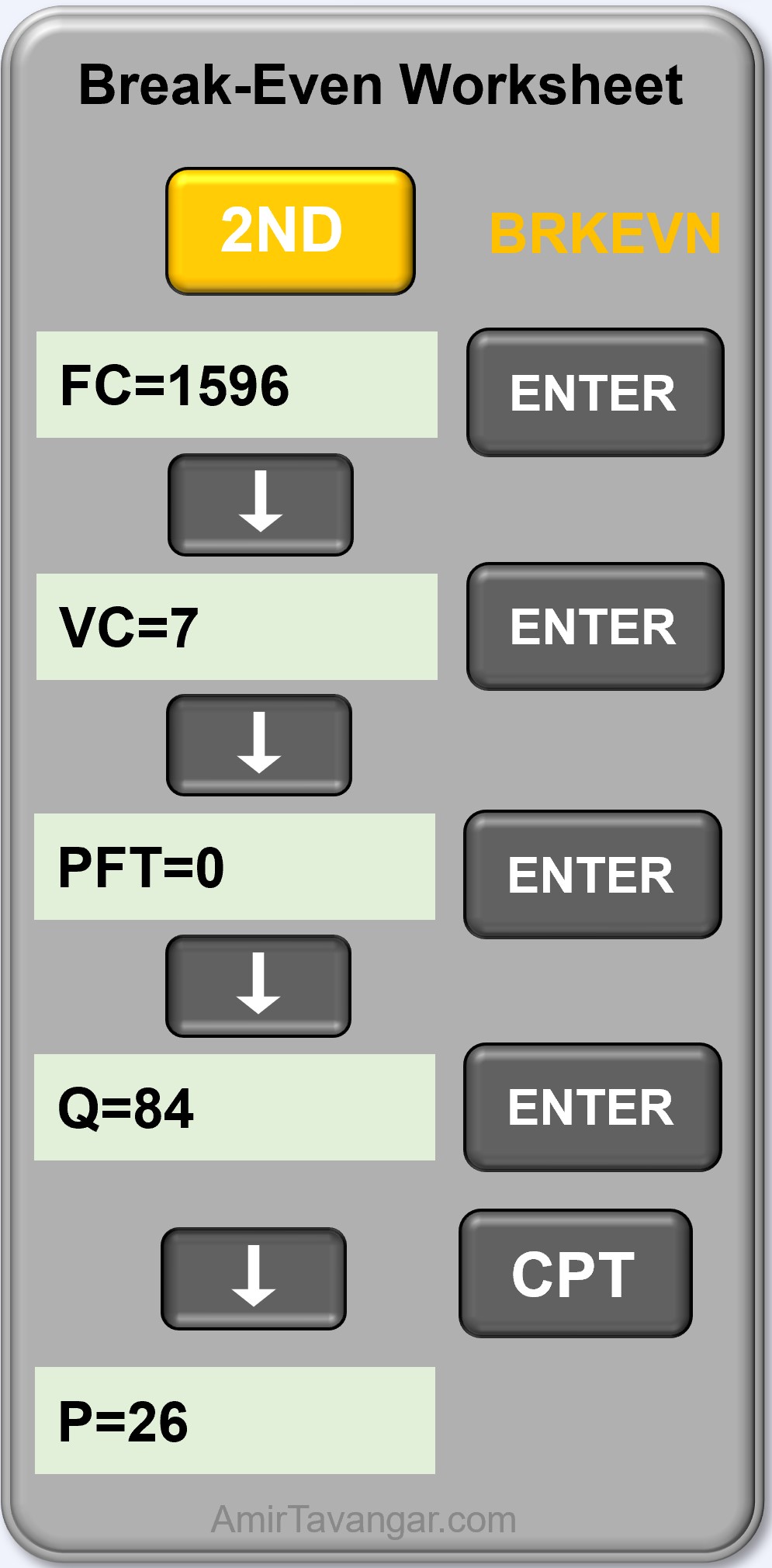
Therefore, Margaret needs to sell each T-shirt at $26 to break even.
b) Break-even in dollars is the total revenue at break-even quantity ([asciimath]X_B=84[/asciimath])
[asciimath]TR=26*X[/asciimath]
[asciimath]TR_B=26(84)[/asciimath]
[asciimath]=$2184[/asciimath]
c) Since the quantity of 60 is less than the quantity at break-even (84), she incurred a loss in February. To determine the extent of this loss, we input 60 for the quantity (Q) and calculate the net income (PFT).

The profit is calculated to be [asciimath]-$456[/asciimath], where the negative sign indicates a loss, and the amount represents the extent of that loss.
Try an Example
Section 6.5 Exercises
- A company offers a product at a price of $61 each. The variable costs amount to $12 for each unit, and the fixed costs total $41,650 per month. a) Determine how many units must be sold each month to reach the break-even point. b) Compute the revenue required to break even, rounding your answer to the nearest cent.
Show/Hide Answer
a) 850 units
b) $51,850.00 - Vibrant Visuals manufactures and sells high-definition cameras for $84 each. The company's annual fixed costs are $54,234. Each camera also carries variable costs of $20 for parts and $18 for assembly labor. a) Calculate the number of cameras that need to be sold for Vibrant Visuals to break even. b) If Vibrant Visuals produced and sold 2245 cameras in a year, determine the company's profit or loss for that year. c) To achieve an annual profit of $143,658, how many cameras must the company sell?
Show/Hide Answer
a) X = 1179 Cameras
b) NI = $49,036; Profit
c) X = 4302 Cameras - A startup company, EcoLight Innovations, specializes in producing eco-friendly desk lamps. The company's fixed costs for operating, including rent, salaries, and utilities, total $36,000 per year. Each desk lamp has variable costs amounting to $15 for materials and $10 for labor. a) If EcoLight Innovations wants to break even by selling 1,200 desk lamps in a year, calculate the selling price per lamp necessary to cover all costs. b) If the company decides to set the selling price at $10 above the break-even price, determine the total profit for the year if they sell 1,500 lamps.
Show/Hide Answer
a) SP = $55
b) NI = $24,000

