Annuities

3.4 PMT of Annuities: Calculator Approach

A. Payment of Ordinary Annuity

In this section, we focus on calculating the periodic payment amount (PMT) required for an annuity. This payment is the amount that is either paid or received regularly throughout the term of the annuity. Depending on the scenario, whether it involves retirement plans, loans, or savings schemes, the calculation of PMT may be based on the Future Value (FV), the Present Value (PV) of the annuity, or a combination of both.

Similar to the previous sections, we use the time-value-of-money (TVM) worksheet in financial calculators for computing the amount of periodic payments in annuity problems. It’s also important to adhere to the cash flow sign convention (see Table 2.2.1 in Section 2.2) when inputting monetary values into the calculator. This ensures consistency and accuracy in our calculations.

As discussed in the previous sections, it’s crucial to first verify the payment timing setting on your calculator before solving annuity problems. The default setting is usually at ‘END’ (end of the payment period), which is appropriate for ordinary annuities. However, for annuities due, where payments are made at the beginning of each period, this setting needs to be adjusted to ‘BGN’ (beginning of the payment period). Refer to Figure 3.2.1 in Section 3.2 to learn how to change the payment timing on a financial calculator.

 

How to Compute the Size of Payment of Annuities Using a Financial Calculator

1. Clear the TVM Worksheet: Before starting, clear your TVM worksheet to remove any previous values by pressing ‘2ND’ followed by the ‘FV’ key.

2. Identify the Type of Annuity: Determine if it’s an ordinary annuity (payments at the end of each period) or an annuity due (payments at the beginning of each period). Adjust your calculator’s setting accordingly (END for ordinary annuities, BGN for annuities due).

3. Input Known Values:

  • Number of Periods (N): Enter the total number of payment periods.
  • Interest Rate per Period (I/Y): Input the nominal interest rate in percent without the percent symbol.
  • Present Value (PV): For loans, enter the loan amount as a positive value (cash inflow). For investments, if there is an initial lump sum, enter it as a negative value (cash outflow). Set to zero if not applicable.
  • Future Value (FV): For investments, enter the desired future value as a positive value (inflow). For loans, like lease agreements, input the residual value as the future value and enter it as a negative value (outflow). Set to zero if not applicable.

4. Calculate PMT: After entering the other values, compute PMT. The calculator will display PMT as a negative number for outflows (e.g., savings, and loan repayments) and a positive number for inflows (e.g., annuity payouts).

 

Example 3.4.1: Compute PMT Given FV of Ordinary Simple Annuity

What deposit made at the end of each month will accumulate to $12,000 in 6 years at 4.8% p.a. compounded monthly?

Show/Hide Solution

Given information

  • Interest is compounded monthly so [asciimath]C//Y = 12[/asciimath]
  • Payments are made at the end of each month so [asciimath]P//Y = 12[/asciimath]
  •  [asciimath]C//Y = P//Y[/asciimath]  [asciimath]=>[/asciimath]  Ordinary Simple Annuity
  • Annuity term: [asciimath]t = 6[/asciimath] years
  • Number of payments in the term: [asciimath]N = P//Y * t = 12(6) = 72[/asciimath]
  • Nominal interest rate: [asciimath]I//Y = 4.8%[/asciimath]
  • The initial balance of the account is zero, so [asciimath]PV = 0[/asciimath]
  • Future value of investments is cash inflow: [asciimath]FV = $12,000[/asciimath]

[asciimath]PMT=?[/asciimath]

TVM Worksheet demonstrating how to compute Payment (PMT). The procedure involves entering each specified value, pressing the corresponding key, and concluding by pressing the 'Compute' key followed by the PMT key to finalize the PMT calculation.

The size of the deposits made must be $144.15.

 

Example 3.4.2: Compute PMT Given PV of Ordinary Simple Annuity

What payment is required at the end of each month for 8 years to repay a $32,000 loan if the interest charged is 3.8% compounded monthly?

Watch Video

 

Show/Hide Solution

Given information

  • Interest is compounded monthly so [asciimath]C//Y = 12[/asciimath]
  • Payments are made at the end of each month so [asciimath]P//Y = 12[/asciimath]
  • [asciimath]C//Y = P//Y[/asciimath]   [asciimath]=>[/asciimath]  Ordinary Simple Annuity
  • Annuity term: [asciimath]t = 8[/asciimath]   years
  • Number of payments in the term: [asciimath]N = P//Y * t = 12(8) = 96[/asciimath]
  • Nominal interest rate: [asciimath]I//Y = 3.8%[/asciimath]
  • In loans, the present value (the loan principal) is cash inflow: [asciimath]PV = $32,000[/asciimath]
  • No remaining balance at the end of the annuity term, so [asciimath]FV=0[/asciimath]

[asciimath]PMT=?[/asciimath]

TVM Worksheet demonstrating how to compute Payment (PMT). The procedure involves entering each specified value, pressing the corresponding key, and concluding by pressing the 'Compute' key followed by the PMT key to finalize the PMT calculation.

Thus, the payments of $387.09 are required to repay the loan.

 

Try an Example

 

 

Example 3.4.3: Compute PMT Given FV of Ordinary General Annuity
Dakota is planning for a renovation project that will cost $95,000. To finance this, she intends to save money in her savings account earning an interest rate of 4.12% compounded quarterly. a) Determine the amount Dakota needs to deposit at the end of each month to reach her goal of $95,000 in 5 years. b) Calculate the total amount Dakota will have deposited into the account over this 5-year period. c) Determine the total interest Dakota will earn on her savings account.
Show/Hide Solution

Given information

  • Interest is compounded quarterly so [asciimath]C//Y = 4[/asciimath]
  • Payments are made at the end of each month so [asciimath]P//Y = 12[/asciimath]
  • [asciimath]C//Y != P//Y[/asciimath]   [asciimath]=>[/asciimath]  Ordinary General Annuity
  • Annuity term: [asciimath]t = 5[/asciimath] years
  • Number of payments in the term: [asciimath]N = P//Y * t = 12(5) = 60[/asciimath]
  • Nominal interest rate: [asciimath]I//Y = 4.12%[/asciimath]
  • The initial balance of the account is zero, so [asciimath]PV = 0[/asciimath]
  • Future value of investments is cash inflow: [asciimath]FV = $95,000[/asciimath]

a) [asciimath]PMT=?[/asciimath]

TVM Worksheet demonstrating how to compute Payment (PMT). The procedure involves entering each specified value, pressing the corresponding key, and concluding by pressing the 'Compute' key followed by the PMT key to finalize the PMT calculation.

Dakota will need to make monthly deposits of $1429.06 to accumulate her desired amount.

 

b) The total amount that Dakota will have deposited over the 5-year term is equal to the number of payments (N) multiplied by the size of each payment (PMT).

[asciimath]"Total amount deposited"=N*PMT[/asciimath]

[asciimath]=60(1429.06)[/asciimath]

 [asciimath]=$85,743.60[/asciimath]

c) [asciimath]I=?[/asciimath] 

Given this is an investment scenario where [asciimath]FV[/asciimath] is known, the total interest amount earned in the savings account is given by Formula 3.2.

 [asciimath]I=FV-(N*PMT)[/asciimath]

[asciimath]=95,000-85,743.60[/asciimath]

[asciimath]=$9256.40[/asciimath]

 

Try an Example

 

 

Example 3.4.4: Compute PMT Given Purchase Price

Jeff purchased a car listed for $29,900. He paid 20% of the cost as a down payment and financed the balance amount at 5.1% compounded monthly for 12 years. a) What is the size of payment made at the end of every three months to settle the loan? b) How much was the amount of interest charged?

Show/Hide Solution

Given information

  • Interest is compounded monthly, so [asciimath]C//Y = 12[/asciimath]
  • Payments are made at the end of every three months so  [asciimath]P//Y = 4[/asciimath]

[asciimath]C//Y != P//Y[/asciimath]   [asciimath]=>[/asciimath]  Ordinary General Annuity

  • Annuity term: [asciimath]t = 12[/asciimath] years
  • Number of payments in the term: [asciimath]N = P//Y * t = 4(12) = 48[/asciimath]
  • Nominal interest rate:[asciimath]I//Y = 5.1%[/asciimath]
  • Purchase price = $29,900
  • Down payment = 20% of the purchase price
  • The loan is fully settled, so [asciimath]FV=0[/asciimath]

a)

Finding PV of loan

First, we need to find the amount of the loan, which is the remaining balance after paying the down payment.

 [asciimath]"Down payment"[/asciimath] [asciimath]=20%(29,900)[/asciimath] [asciimath]=$5980[/asciimath]

Using Formula 3.5, we have

 [asciimath]"Purchase Price" = "Down payment" + PV[/asciimath]

Rearranging the equation for [asciimath]PV[/asciimath]gives

 [asciimath]PV = "Purchase Price"-"Down payment"[/asciimath]

 [asciimath]PV=29,900-5980[/asciimath]

 [asciimath]=$23,920[/asciimath]

Next, we use the PV and other given values to compute the size of the payments. We use the calculator approach.

TVM Worksheet demonstrating how to compute Payment (PMT). The procedure involves entering each specified value, pressing the corresponding key, and concluding by pressing the 'Compute' key followed by the PMT key to finalize the PMT calculation.

The size of the quarterly payments is $670.15.

b) The amount of interest for loans is given by Formula 3.4.

 [asciimath]I=N.PMT-PV[/asciimath]

 [asciimath]=48(670.15)-23,920[/asciimath]

[asciimath]=32,167.2-23,920[/asciimath]

 [asciimath]=$8247.20[/asciimath]

 

Example 3.4.5: Compute PMT Given Both FV and PV

Inesh has already saved $11,600 in his savings account as of today, and he plans to contribute equal deposits at the end of each month for the next 10 years. What monthly deposit is required to accumulate $105,000 in total at the end of the 10 years assuming the account earns 5.2% compounded annually?

Show/Hide Solution

Given information

  • Interest is compounded quarterly so [asciimath]C//Y = 1[/asciimath]
  • Payments are made at the end of each month so [asciimath]P//Y = 12[/asciimath]
  •  [asciimath]C//Y != P//Y[/asciimath]   [asciimath]=>[/asciimath]  Ordinary General Annuity
  • Investment term: [asciimath]t = 10[/asciimath]  years
  • Number of payments in the term: [asciimath]N = P//Y * t = 12(10) = 120[/asciimath]
  • Nominal interest rate: [asciimath]I//Y = 5.2%[/asciimath]
  • In investments, the future value is cash inflow (received), so [asciimath]FV = $105,000[/asciimath]
  • In investments, the present value is cash outflow (invested), so [asciimath]PV = -$11,600[/asciimath]

[asciimath]PMT=?[/asciimath]

The accumulated value at the end of the term consists of two components: the future values of all the periodic payments ([asciimath]FV_("PMT")[/asciimath]) and the future value of the initial lump sum investment ([asciimath]FV_("PV")[/asciimath]).

 [asciimath]FV=FV_("PMT")+FV_("PV")[/asciimath]

Timeline depicting contributions to the account with 120 monthly payments (PMTs) ending at the end of year 10, plus an initial account balance at the beginning of the investment (PV). Arrows from the payments and the initial balance direct to year 10, highlighting the requirement to calculate their future values.

To calculate the size of each periodic payment, we must first determine [asciimath]FV_("PMT")[/asciimath], the future value of these payments. Knowing that the combined future value of the periodic payments and the initial lump sum equals the target accumulation of $105,000, our first step is to calculate the future value of the initial lump sum ([asciimath]FV_("PV")[/asciimath]). This amount is then subtracted from the desired accumulated total of $105,000.

Using a financial calculator simplifies this process, as it can compute the periodic payment in a single step.

Visualization of a TVM worksheet for calculating Payment (PMT), using initial savings as Present Value (PV), marked as a negative value to signify cash outflow, and the goal accumulated value as Future Value (FV), marked as a positive value indicating cash inflow. The steps include entering each given value, then pressing the corresponding key, and finalizing the PMT calculation by pressing the 'Compute' button followed by the PMT button.

Monthly deposits of $549.81 are needed to accumulate to the desired amount.

Note that the present value (PV) should be input as a negative number, as it represents a cash outflow – money leaving Inesh’s possession and going into the account. Conversely, the future value (FV) is entered as a positive value, indicating a cash inflow, which is the amount Inesh will receive at the end of the term.

 

Try an Example

 

B. Payment of Annuity Due

In the following examples, we will focus on calculating the periodic payments of annuities due. In these annuities, since payments are made at the start of each payment period, it is important to change the payment timing setting on your calculator to ‘BGN’ (beginning of the payment period).

 

Example 3.4.6: Compute PMT Given PV of Simple Annuity Due

What monthly rent payment at the beginning of each month for three years is needed to fulfill a lease contract that is worth $10,000 if money is worth 5% compounded monthly?

Show/Hide Solution

Given information

  • Interest is compounded monthly so [asciimath]C//Y = 12[/asciimath]
  • Payments are made at the beginning of each month so [asciimath]P//Y = 12[/asciimath]
  •  [asciimath]C//Y = P//Y[/asciimath]   [asciimath]=>[/asciimath]  Simple Annuity Due
  • Annuity term: [asciimath]t = 3[/asciimath] years
  • Number of payments in the term: [asciimath]N = P//Y * t = 12(3) = 36[/asciimath]
  • Nominal interest rate: [asciimath]I//Y = 5%[/asciimath]
  • The present value is received, so it is cash inflow: [asciimath]PV = $10,000[/asciimath]
  • [asciimath]FV=0[/asciimath]

[asciimath]PMT=?[/asciimath]

TVM Worksheet demonstrating how to compute Payment (PMT). Instructions include setting payment timing to 'BGN' for annuities due. The steps include entering each given value, then pressing the corresponding key, and finalizing the PMT calculation by pressing the 'Compute' button followed by the PMT button.

Monthly rents of $298.47 are required to fulfill the lease contract.

 

Try an Example

 

 

Example 3.4.7: Compute PMT Given Both PV and FV

Colleen entered into a lease agreement for a car with a list price of $42,000, which is expected to have a residual value of $21,450 after four years. She agreed to make a down payment of 10% of the car’s list price. Given an interest rate of 2.8% compounded monthly, calculate the amount of Colleen’s lease payment that is due at the beginning of each week.

Note: The residual value of a leased vehicle represents an estimate of how much the car will be worth at the end of the lease term.

Show/Hide Solution

Given information

  • Interest is compounded monthly so [asciimath]C//Y = 12[/asciimath]
  • Payments are made at the beginning of every week so [asciimath]P//Y = 52[/asciimath]
  • [asciimath]C//Y != P//Y[/asciimath]   [asciimath]=>[/asciimath]  General Annuity Due
  • Annuity term: [asciimath]t = 4[/asciimath]   years
  • Number of payments in the term: [asciimath]N = P//Y * t = 52(4) = 208[/asciimath]
  • Nominal interest rate: [asciimath]I//Y = 2.8%[/asciimath]
  • List price [asciimath]= $42,000[/asciimath]
  • Down payment [asciimath]= 10%[/asciimath] of the list price
  • Residual value [asciimath]= $21,450[/asciimath]

Finding PV of loan

The residual value of the car is the estimated value of the car at the end of the lease term, i.e., in four years. So it is considered a future value. We need to find the amount of the loan without considering the residual value, which is the remaining balance after paying the down payment. Using Formula 3.5, we have

 [asciimath]"List Price" = "Down payment" + PV[/asciimath]

Rearranging the equation for [asciimath]PV[/asciimath]gives

 [asciimath]PV = "List Price"-"Down payment"[/asciimath]

 [asciimath]PV=42,000-10%(42,000)[/asciimath]

 [asciimath]=$37,800[/asciimath]

Next, we use the above PV, residual as FV, and other given values to compute the size of the payment.

 

Visualization of a TVM worksheet for calculating Payment (PMT), using the loan amount as Present Value (PV), marked as a positive value to signify cash inflow, and the residual value as Future Value (FV), marked as a negative value indicating cash outflow. Instructions include setting payment timing to 'BGN' for annuities due. The steps include entering each given value, then pressing the corresponding key, and finalizing the PMT calculation by pressing the 'Compute' button followed by the PMT button.

The size of the weekly payments is $94.60.

Notice that PV is entered as a positive value since it is considered a cash inflow (Colleen receives the lease loan), and FV is entered as a negative value since Colleen would have to return the car (equivalent to the residual value) or pay the residual value to own the car (if such an option is offered) at the end of the lease term (cash outflow).

 

Try an Example

 

C. Payments in Scenarios with Multiple Annuities

The following example delves into calculating payments for a scenario involving a Registered Retirement Savings Plan (RRSP) and a Registered Retirement Income Fund (RRIF). Before we begin, it is beneficial to introduce these concepts.

RRSP and RRIF are fundamental components of Canada’s retirement savings system, designed to help individuals save for their future. The RRSP is a savings account with tax advantages to encourage saving for retirement. Contributions to an RRSP are tax-deductible, meaning they can reduce the amount of income tax you pay in the year you make the contribution. Once you retire, RRSP is converted into a RRIF which provides you with a regular income during retirement. Withdrawals from an RRIF are taxed as income at your marginal tax rate. The frequency of these withdrawals can be monthly, quarterly, semi-annually, or annually, offering flexibility in managing retirement income.

 

Example 3.4.8: Compute PMT of First Term Given PMT of the Second Term

Darius is planning for his retirement, which is 30 years away, by making end-of-quarter contributions to his Registered Retirement Savings Plan (RRSP), set to later convert into a Registered Retirement Income Fund (RRIF). Upon retirement, he intends to withdraw $3,400 at the end of each month for 20 years. An annual interest rate of 4.8%, compounded monthly, applies to both the RRSP during the accumulation phase and the RRIF during the distribution phase.

a) What is the total amount Darius must have in his RRIF at the start of retirement to support his goal of monthly withdrawals of $3,400?

b) How much must Darius deposit into his RRSP at the end of each quarter to ensure he accumulates the required amount in his RRIF by his retirement in 30 years?

Show/Hide Solution

Timeline illustrating Darius's retirement planning over a 50-year span. The first 30 years show quarterly RRSP contributions leading up to retirement, marked at year 30. At this point, the timeline transitions to depict the conversion of the RRSP into a RRIF. The next 20 years illustrate monthly withdrawals of $3,400 from the RRIF, ending at year 50. Key points include the start of RRSP contributions (Year 0), conversion to RRIF at retirement (Year 30), and the duration of RRIF withdrawals (20 years).

a) Term 2: RRIF – Ordinary Simple Annuity

To determine the total amount Darius needs in his RRIF at the start of retirement to afford monthly withdrawals of $3,400 for 20 years, we calculate the present value of those payments at the time of retirement.

Given Information

  • Interest is compounded monthly so [asciimath]C//Y = 12[/asciimath]
  • Withdrawals are made at the end of every month so [asciimath]P//Y_2 = 12[/asciimath]
  •  [asciimath]C//Y = P//Y_2[/asciimath]  [asciimath]=>[/asciimath]   Ordinary Simple Annuity
  • RRIF term: [asciimath]t_2 = 20[/asciimath] years
  • Number of payments in the term: [asciimath]N_2 =P//Y_2*t_2=12 (20) = 240[/asciimath]
  • Nominal interest rate: [asciimath]I//Y = 4.8%[/asciimath]
  • The payments are received and are cash inflow, so [asciimath]PMT_2 = $3400[/asciimath]
  • The fund will be depleted by the end of the term, so [asciimath]FV_2 = 0[/asciimath]

[asciimath]PV_2=?[/asciimath]

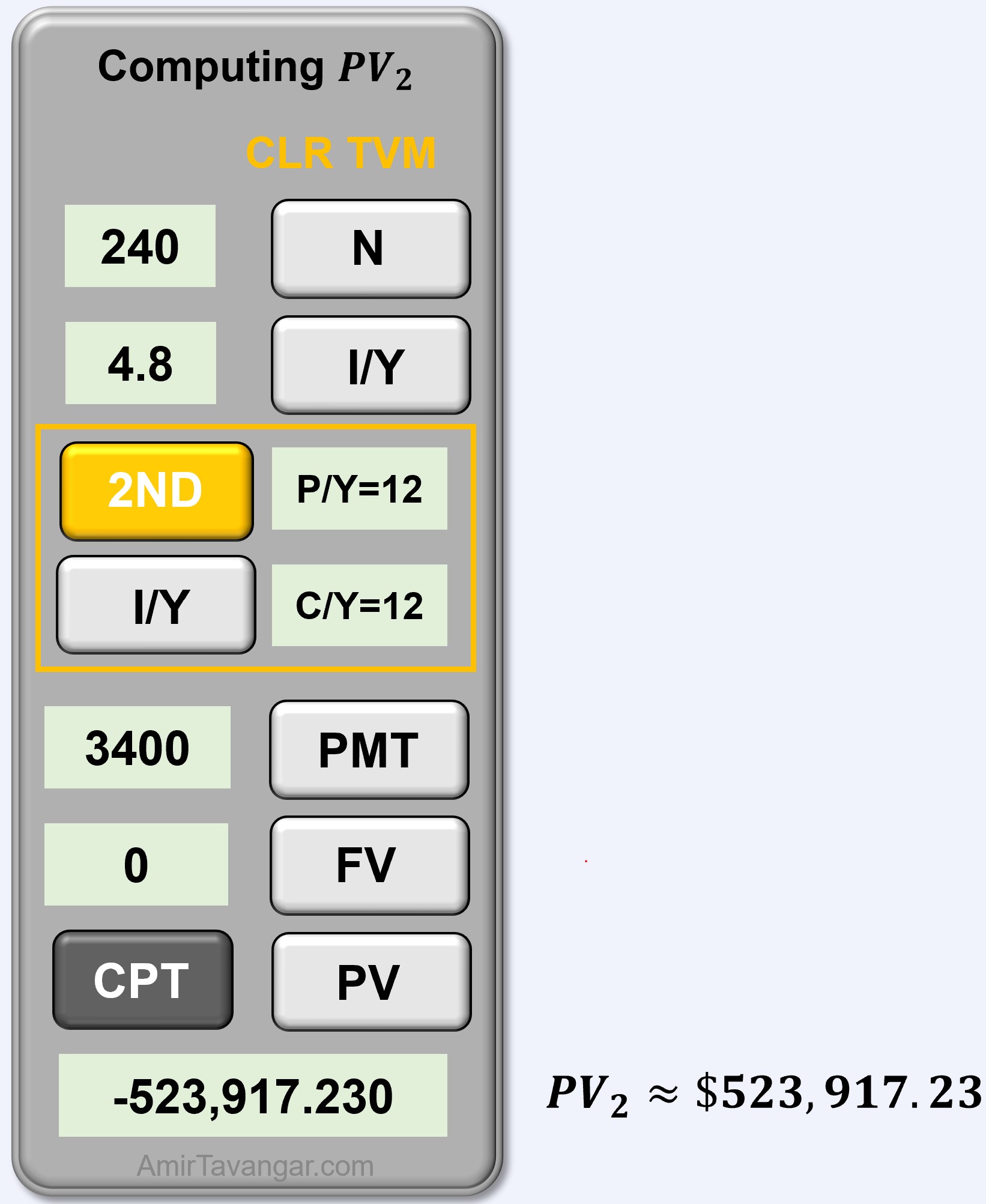
Visualization of a TVM worksheet for calculating present value (PV2) of RRIF term, using the $3400 withdrawals as PMT, marked as a positive value to signify cash inflow. The steps include entering each given value, then pressing the corresponding key, and finalizing the PV calculation by pressing the 'Compute' button followed by the PV button.

Therefore, the total amount Darius must have in his RRIF at the start of retirement to support his goal is $523,917.23.

b) Term 1: RRSP – Ordinary General Annuity

The value needed at retirement, determined in Part (a) becomes the target FV for the RRSP contributions. We then calculate the quarterly contribution Darius must make to his RRSP over 30 years to accumulate to that target FV at retirement.

Given Information

  • Interest is compounded monthly so [asciimath]C//Y = 12[/asciimath]
  • Withdrawals are made at the end of every quarter so [asciimath]P//Y_1 = 4[/asciimath]
  •  [asciimath]C//Y != P//Y_1[/asciimath]  [asciimath]=>[/asciimath]   Ordinary General Annuity
  • RRSP term: [asciimath]t_1 = 30[/asciimath] years
  • Number of payments in the term: [asciimath]N_1 =P//Y_1*t_1=4 (30) = 120[/asciimath]
  • Nominal interest rate: [asciimath]I//Y = 4.8%[/asciimath]
  • No initial balance in RRSP, so [asciimath]PV_1 = 0[/asciimath]
  • In investments, the future value is cash inflow, so [asciimath]FV_1 = PV_2=$523,917.230...[/asciimath]  (use unrounded value for accuracy)

[asciimath]PMT_1=?[/asciimath]

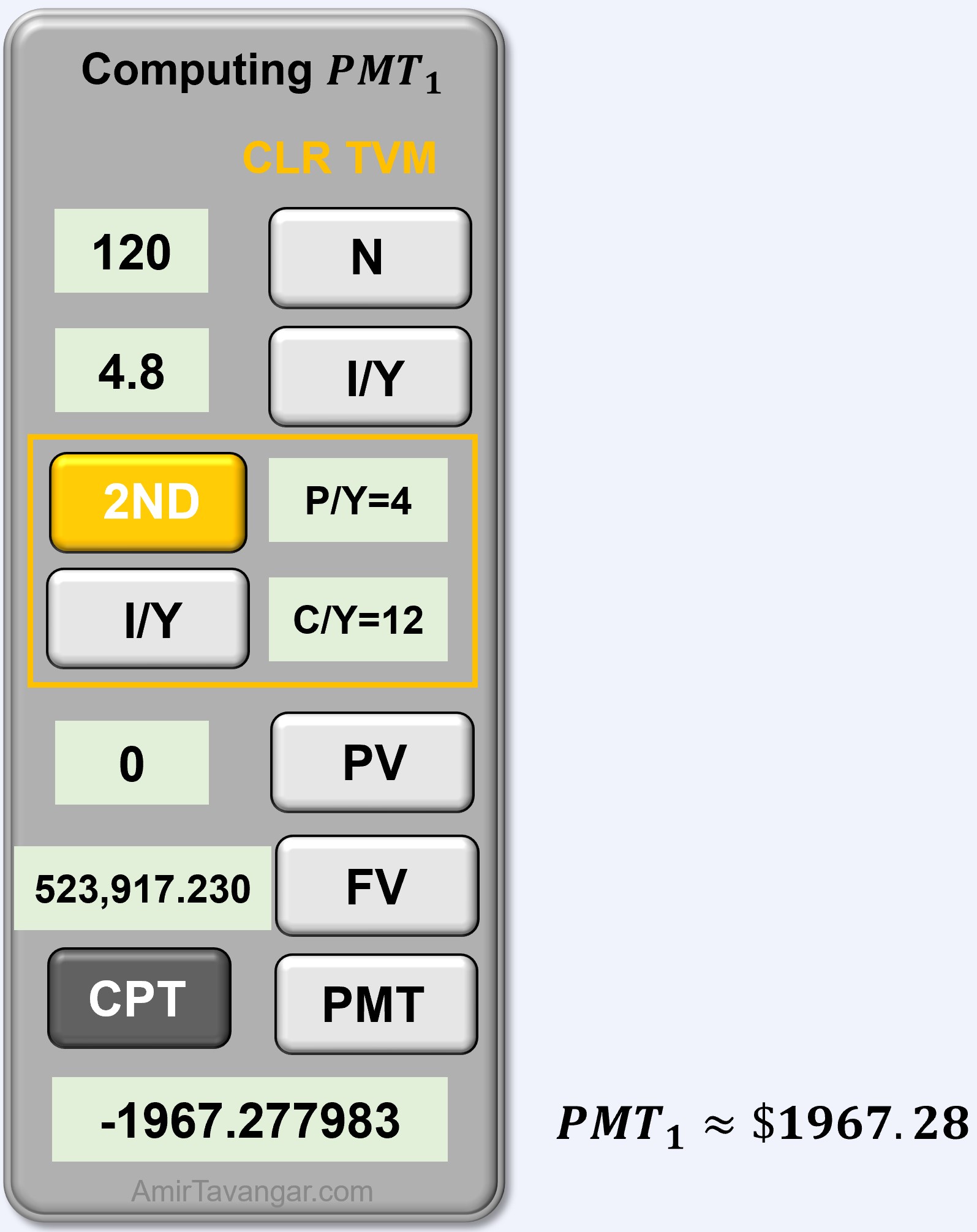
Visualization of a TVM worksheet for calculating required payments (PMT1) of RRSP term, using PV2, determined in Part (a) as future Value (FV1) with a positive sign for cash inflow. The steps include entering each given value, then pressing the corresponding key, and finalizing the PMT calculation by pressing the 'Compute' button followed by the PMT button.

Thus, Darius will need to make quarterly deposits of $1967.28 to ensure he accumulates the required amount in his RRIF by his retirement.

 

Try an Example

 

Section 3.4 Exercises

  1. What payment is required at the end of every month for 5.5 years to repay a $11,968 loan if interest is 4.4% compounded monthly?
    Show/Hide Answer

     

    PMT = $204.49

  2. Gregory purchased a car for $53,500; he paid 5% of the cost as a down payment and financed the balance amount at 3.5% compounded monthly for 3 years. a) What is the size of payment made at the end of every month to settle the loan? b) What was the amount of interest charged?
    Show/Hide Answer

     

    a) PMT = $1,489.28

    b) I = $2,789.08

  3. To fulfill a lease contract valued at $29,000, rent payments are required at the beginning of each month for 5 years. The interest rate on this lease is assumed to be 4.79%, compounded monthly. a) What is the size of the payments? b) How much interest was charged on the lease?
    Show/Hide Answer

     

    a) PMT = $542.32

    b) I = $3,539.20

  4. Dawn entered into a lease agreement for a car with a list price of $56,460.00, which is expected to have a residual value of $31,053 after 6 years. She agreed to make a down payment of 15% of the car’s list price. Given an interest rate of 2.06% compounded semi-annually, calculate the amount of Dawn’s lease payment that is due at the beginning of each month.
    Show/Hide Answer

     

    PMT = $302.79

  5. Kristina has already saved $7,600 in her savings account as of today, and she plans to contribute equal deposits at the end of each year for the next 10 years. What deposit is required to accumulate $91,500 in total at the end of the 10 years assuming the account earns 2.42% compounded quarterly?
    Show/Hide Answer

     

    PMT = $7323.15

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Mathematics of Finance Copyright © 2024 by Amir Tavangar is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book