Annuities
3.10 Number of Payments and Time: Formula Approach
A. Number of Payments and Time of Annuities
Suppose you are setting aside funds for a renovation project with a target of $50,000. You plan to save $100 every week and deposit it into your savings account. The key question is how long will it take to reach your $50,000 savings goal. To find this out, you need to first calculate the number of weekly payments (N) you must make to accumulate the desired amount. Once you have determined N, you will know the exact duration required to achieve your savings target for the renovation project.
In this section, we turn our attention to computing the total number of payments in annuities (N) and understanding how long it takes for an annuity to achieve its financial objectives, whether it's accumulating a desired sum for retirement, paying off a loan, or reaching a specific investment goal.
When the time of the annuity term (t) is unknown, the initial step is to calculate N using either a formula or a financial calculator. Once N is known, it can then be used to work out the time. Depending on the scenario, whether it involves retirement plans, loans, or savings schemes, the calculation of N may be based on the Periodic Payment (PMT) and either the Future Value (FV), the Present Value (PV) of the annuity, or a combination of both.
It is important to note that in annuities calculations, unlike compound interest calculation where N is the number of compounding periods in the term, N represents the number of payments in the term. This value is always rounded up to the next whole number of payments, which may result in the last payment being smaller than the others.
Once N is computed, the annuity's term (t) can be determined by rearranging Formula 3.1a.
[asciimath]t=N/(P//Y)[/asciimath]Formula 3.1b
B. Number of Payments of Ordinary Simple Annuity
If FV is known, we can rearrange the FV formula for an ordinary simple annuity (Formula 3.5a) to solve for the unknown number of payments in the term, N.
[asciimath]N=(ln[1+(FV*i)/(PMT)])/(ln(1+i))[/asciimath]Formula 3.5c
Similarly, if the present value (PV) is known, we can adjust the PV formula (Formula 3.9a) to determine the unknown number of payments in the term, N.
[asciimath]N=-(ln[1-(PV*i)/(PMT)])/(ln(1+i))[/asciimath]Formula 3.9c
Mahsa wants to save $80,000 for her house down payment. Suppose she plans to make deposits of $1,290 at the end of every three months into an account earning 4.7% compounded quarterly. a) How many deposits will she have to make to achieve her goal? b) How long will it take? Give the time in terms of years and months.
Show/Hide Solution
Given Information
- Interest is compounded quarterly so [asciimath]C//Y = 4[/asciimath]
- Payments are made at the end of every three months so [asciimath]P//Y = 4[/asciimath]
[asciimath]C//Y = P//Y[/asciimath] [asciimath]=>[/asciimath] Ordinary Simple Annuity
- Nominal interest rate: [asciimath]I//Y = 4.7%[/asciimath]
- Periodic interest rate: [asciimath]i = (I//Y)/(C//Y) = (4.7%)/4 =1.175%[/asciimath]
- Periodic payments: [asciimath]PMT = $1,290[/asciimath]
- The initial balance of the account is zero, so [asciimath]PV = 0[/asciimath]
- Future value: [asciimath]FV = $80,000[/asciimath]
a) [asciimath]N=?[/asciimath]
Given the future value is known, we use Formula 3.5c to calculate the number of payments:
[asciimath]N=(ln[1+(FV*i)/(PMT)])/(ln(1+i))[/asciimath]
[asciimath]N=(ln[1+(80,000(0.01175))/(1290)])/(ln(1+0.01175))[/asciimath]
[asciimath]=46.856...[/asciimath]
[asciimath]=47[/asciimath]
The number of payments in the term, N, is rounded up to 47 deposits.
b) [asciimath]t=?[/asciimath]
To find the time period of the term, we substitute N and P/Y into Formula 3.1b:
[asciimath]t=N/(P//Y)[/asciimath]
[asciimath]t=47/4[/asciimath]
[asciimath]=11.75[/asciimath] years
[asciimath]=11[/asciimath] years [asciimath]+ 0.75(12)[/asciimath] months
[asciimath]=11[/asciimath] years and [asciimath]9[/asciimath] months
Note: In annuities, N represents the number of payments in the term and its value is always rounded up to the next whole number of payments regardless of the decimal part of the calculated N.
Try an Example
Mahsa already has $25,000 in her savings account, and she wants this to accumulate to $80,000 for a house down payment. Suppose she plans to make deposits of $1,290 at the end of every three months into the account earning 4.7% compounded quarterly. a) How many deposits will she have to make to achieve her goal? b) How long will it take? Give the time in terms of years and months.
Show/Hide Solution
Given Information
- Interest is compounded quarterly so [asciimath]C//Y = 4[/asciimath]
- Payments are made at the end of every three months so [asciimath]P//Y = 4[/asciimath]
[asciimath]C//Y = P//Y[/asciimath] [asciimath]=>[/asciimath] Ordinary Simple Annuity
- Nominal interest rate: [asciimath]I//Y = 4.7%[/asciimath]
- Periodic interest rate: [asciimath]i = (I//Y)/(C//Y) = (4.7%)/4 =1.175%[/asciimath]
- Periodic payments: [asciimath]PMT = $1,290[/asciimath]
- Present value is the initial lumpsum invested: [asciimath]PV = $25,000[/asciimath]
- Future value: [asciimath]FV = $80,000[/asciimath]
a) [asciimath]N=?[/asciimath]
The accumulated value of $80,000 is the sum of the future value of the initial investment of $,25,000 ([asciimath]FV_("PV")[/asciimath]) and the future value of the payments ([asciimath]FV_("PMT")[/asciimath]). We can plug in the formulas for the future value of the ordinary simple annuity and the compound interest into the following equation and solve for N.
It is crucial to recognize that in the case of a simple annuity, the number of payments and the number of compounding periods within the term are identical. As a result, the [asciimath]N[/asciimath] variable used in both formulas is the same. However, if we were dealing with a general annuity, it would be necessary to express each [asciimath]N[/asciimath] in terms of time and solve for the time first.
[asciimath]FV=FV_("PV")+[/asciimath] [asciimath]FV_("PMT")[/asciimath]
[asciimath]FV=PV(1+i)^N+[/asciimath][asciimath]PMT[((1+i)^N-1)/i][/asciimath]
We can rearrange the equation for [asciimath]N[/asciimath]:
[asciimath]N=ln((FV*i+PMT)/(PV*i+PMT))/ln(1+i)[/asciimath]
[asciimath]N=ln((80,000(0.01175 )+1290)/(25,000(0.01175 )+1290))/ln(1+0.01175 )[/asciimath]
[asciimath]=29.294...[/asciimath]
[asciimath]=30[/asciimath] (Rounded up)
The number of payments in the term, [asciimath]N[/asciimath], is rounded up to 30 deposits.
b) [asciimath]t=?[/asciimath]
To find the time period of the term, we substitute [asciimath]N[/asciimath] and [asciimath]P//Y[/asciimath] into Formula 3.1b:
[asciimath]t=N/(P//Y)[/asciimath]
[asciimath]t=30/4[/asciimath]
[asciimath]=7.5[/asciimath] years
[asciimath]=7[/asciimath] years [asciimath]+ 0.5(12)[/asciimath] months
[asciimath]=7[/asciimath] years and [asciimath]6[/asciimath] months
Try an Example
C. Number of Payments of Ordinary General Annuity
Like an ordinary simple annuity, when FV is known, we can rearrange the FV formula for an ordinary general annuity (Formula 3.6a) to solve for the unknown number of payments in the term, N.
[asciimath]N=(ln[1+(FV*i_2)/(PMT)])/(ln(1+i_2))[/asciimath]Formula 3.6c
Likewise, if the present value (PV) is known, we can use the PV formula (Formula 3.10a) to determine the unknown number of payments in the term, N.
[asciimath]N=-(ln[1-(PV*i_2)/(PMT)])/(ln(1+i_2))[/asciimath]Formula 3.10c
Where [asciimath]i_2[/asciimath] is the interest rate per payment period
[asciimath]i_2=(1+i)^((C//Y)/(P//Y))-1[/asciimath]
Emanuel won a lottery prize of $1,000,000 and invested it in a fund that earns 4% interest compounded monthly. He plans to withdraw $1,000 at the end of each week. a) Determine the total number of withdrawals Emanuel will make. b) How long will the money last with these weekly withdrawals? Give the time in terms of years and weeks.
Show/Hide Solution
Given Information
- Interest is compounded annually so [asciimath]C//Y = 12[/asciimath]
- Withdrawals are at the end of every week so [asciimath]P//Y = 52[/asciimath]
[asciimath]C//Y != P//Y[/asciimath] [asciimath]=>[/asciimath] Ordinary General Annuity
- Nominal interest rate: [asciimath]I//Y = 4%[/asciimath]
- Periodic interest rate: [asciimath]i = (I//Y)/(C//Y) = (4%)/12 =0.bar(3)%[/asciimath]
- Periodic payments: [asciimath]PMT = $1000[/asciimath]
- Present value: [asciimath]PV = $1,000,000[/asciimath]
- The fund will be fully depleted at the end of the term, so [asciimath]FV=0[/asciimath]
a) [asciimath]N=?[/asciimath]
First, we should find the interest rate per payment period [asciimath]i_2[/asciimath]:
[asciimath]i_2=(1+i)^((C//Y)/(P//Y) )-1[/asciimath]
[asciimath]i_2=(1+0.00bar(3))^(12/52)-1[/asciimath]
[asciimath]=0.000768246...[/asciimath]
Given the present value is known, we then use Formula 3.10c to calculate the number of payments:
[asciimath]N=-(ln[1-(PV*i_2)/(PMT)])/(ln(1+i_2))[/asciimath]
[asciimath]N=-(ln[1-(1,000,000(0.000768246... ))/(1000)])/(ln(1+0.000768246... ))[/asciimath]
[asciimath]=1903.8...[/asciimath]
[asciimath]=1904[/asciimath] (Rounded up)
The number of payments in the term, N, is rounded up to 1904 withdrawals.
b) [asciimath]t=?[/asciimath]
To find the time period of the term, we substitute N and P/Y into Formula 3.1b:
[asciimath]t=N/(P//Y)[/asciimath]
[asciimath]t=1904/52[/asciimath]
[asciimath]=36.6153...[/asciimath] years
[asciimath]=36[/asciimath] years [asciimath]+ 0.6153... (52)[/asciimath] weeks
[asciimath]=36[/asciimath] years and [asciimath]32[/asciimath] weeks
D. Number of Payments of Simple Annuity Due
If the FV of a simple annuity due is known, we can rearrange the FV formula for such an annuity (Formula 3.7a) to solve for the unknown number of payments in the term, N.
[asciimath]N=(ln[1+(FV*i)/(PMT*(1+i))])/(ln(1+i))[/asciimath]Formula 3.7c
Similarly, if the present value (PV) is known, we can adjust the PV formula (Formula 3.11a) to determine the unknown number of payments in the term, N.
[asciimath]N=-(ln[1-(PV*i)/(PMT*(1+i))])/(ln(1+i))[/asciimath]Formula 3.11c
Esmeralda wants to accumulate $71,000 for her condominium down payment. She plans to make deposits of $3,890 at the beginning of every three months into her savings account, which earns interest at 5.29% compounded quarterly. a) How many deposits will she have to make to achieve her goal? b) How long will it take? Give the time in terms of years and months.
Show/Hide Solution
Given Information
- Interest is compounded quarterly so [asciimath]C//Y = 4[/asciimath]
- Payments are made at the beginning of every three months so [asciimath]P//Y = 4[/asciimath]
[asciimath]C//Y = P//Y[/asciimath] [asciimath]=>[/asciimath] Simple Annuity Due
- Nominal interest rate: [asciimath]I//Y = 5.29%[/asciimath]
- Periodic interest rate: [asciimath]i = (I//Y)/(C//Y) = (5.29%)/4 =1.3225%[/asciimath]
- Periodic payments: [asciimath]PMT = $3,890[/asciimath]
- Initial account balance is zero, so [asciimath]PV=0[/asciimath]
- Accumulated value: [asciimath]FV = $71,000[/asciimath]
a) [asciimath]N=?[/asciimath]
Given the future value is known, we use Formula 3.7c to calculate the number of payments:
[asciimath]N=(ln[1+(FV*i)/(PMT*(1+i))])/(ln(1+i))[/asciimath]
[asciimath]N=(ln[1+(71,000(0.013225))/(3890(1+0.013225 ))])/(ln(1+0.013225 ))[/asciimath]
[asciimath]=16.26...[/asciimath]
[asciimath]=17[/asciimath] (Rounded up)
The number of payments in the term, N, is rounded up to 17 deposits.
b) [asciimath]t=?[/asciimath]
To find the time period of the term, we substitute N and P/Y into Formula 3.1b:
[asciimath]t=N/(P//Y)[/asciimath]
[asciimath]t=17/4[/asciimath]
[asciimath]=4.25[/asciimath] years
[asciimath]=4[/asciimath] years [asciimath]+ 0.25(12)[/asciimath] months
[asciimath]=4[/asciimath] years and [asciimath]3[/asciimath] months
Try an Example
E. Number of Payments of General Annuity Due
When the FV of a general annuity due is known, we can rearrange the FV formula for such an annuity (Formula 3.8a) to solve for the unknown number of payments in the term, N.
[asciimath]N=(ln[1+(FV*i_2)/(PMT*(1+i_2))])/(ln(1+i_2))[/asciimath] Formula 3.8c
Likewise, when the present value (PV) is known, we can rearrange the PV formula (Formula 3.12a) to determine the unknown number of payments in the term, N.
[asciimath]N=-(ln[1-(PV*i_2)/(PMT*(1+i_2))])/(ln(1+i_2))[/asciimath] Formula 3.12c
Where [asciimath]i_2[/asciimath] is the interest rate per payment period
[asciimath]i_2=(1+i)^((C//Y)/(P//Y))-1[/asciimath]
Dario recently retired and has $500,000 in his retirement fund, which earns an annual interest rate of 8% compounded annually. He intends to withdraw $4,000 at the beginning of every month. a) Calculate the total number of withdrawals Dario will make. b) How long will it take for the fund to be depleted?
Show/Hide Solution
Given Information
- Interest is compounded annually so [asciimath]C//Y = 1[/asciimath]
- Payments are withdrawn at the beginning of every month so [asciimath]P//Y = 12[/asciimath]
[asciimath]C//Y != P//Y[/asciimath] [asciimath]=>[/asciimath] General Annuity Due
- Nominal interest rate: [asciimath]I//Y = 8%[/asciimath]
- Periodic interest rate: [asciimath]i = (I//Y)/(C//Y) = (8%)/1 =8%[/asciimath]
- Periodic payments: [asciimath]PMT = $4,000[/asciimath]
- Present value: [asciimath]PV = $500,000[/asciimath]
- The fund balance at the end of the term will be zero, so [asciimath]FV=0[/asciimath]
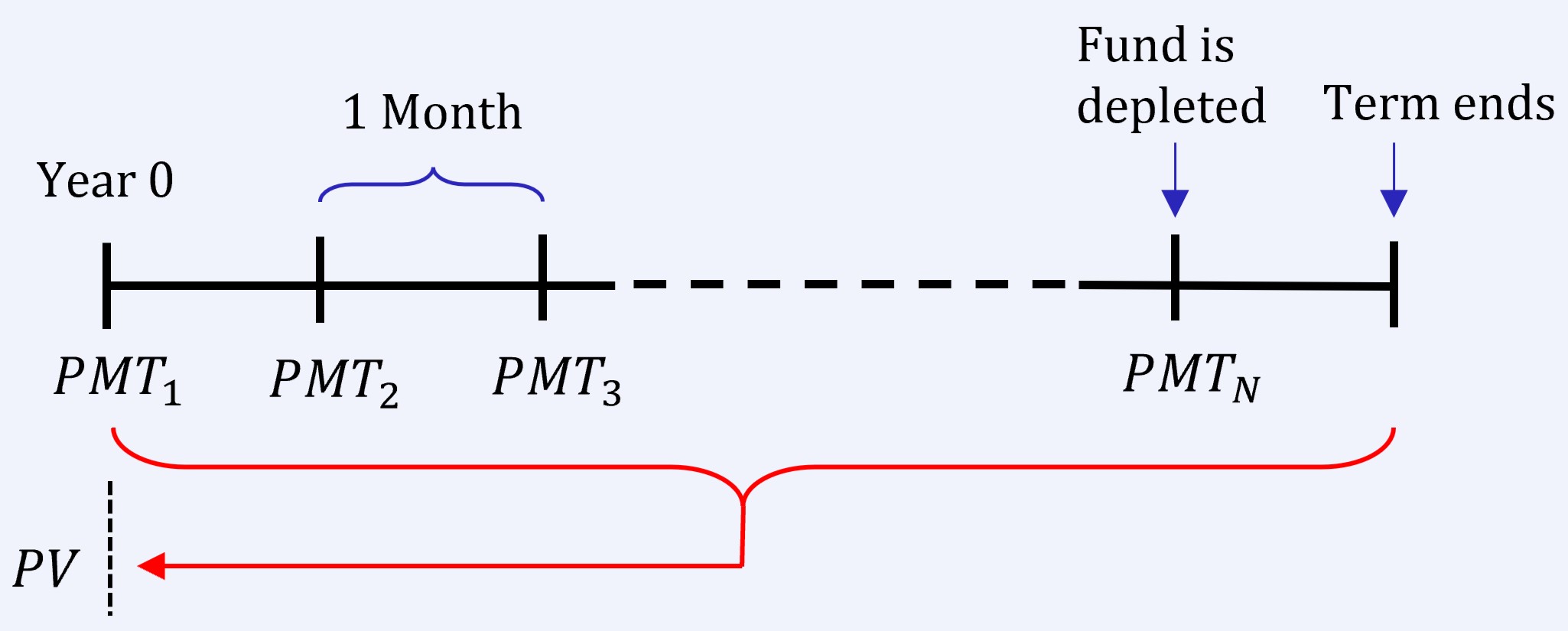
a) [asciimath]N=?[/asciimath]
We should first find the interest rate per payment period [asciimath]i_2[/asciimath]:
[asciimath]i_2=(1+i)^((C//Y)/(P//Y) )-1[/asciimath]
[asciimath]i_2=(1+0.08)^(1/12)-1[/asciimath]
[asciimath]=0.00643403...[/asciimath]
Given the present value is known, we use Formula 3.12c to find the number of payments.
[asciimath]N=-(ln[1-(PV*i_2)/(PMT*(1+i_2))])/(ln(1+i_2))[/asciimath]
[asciimath]N=-(ln[1-(500,000(0.00643403... ))/(4000(1+0.00643403... ))])/(ln(1+0.00643403... ))[/asciimath]
[asciimath]=250.2...[/asciimath]
[asciimath]=251[/asciimath] (Rounded up)
The number of payments in the term, N, is rounded up to 251 withdrawals.
b) [asciimath]t=?[/asciimath]
To find the duration of the annuity term, we substitute N and P/Y into Formula 3.1b:
[asciimath]t=N/(P//Y)[/asciimath]
[asciimath]t=251/12[/asciimath]
[asciimath]=20.91bar(6)[/asciimath] years
[asciimath]=20[/asciimath] years [asciimath]+ 0.91bar6(12)[/asciimath] months
[asciimath]=20[/asciimath] years and [asciimath]11[/asciimath] months
As shown in the timeline, in an annuity due, the term extends beyond the last withdrawal by one period (in this case, one month). Because our focus is on the timeframe up to the final withdrawal (when the fund is depleted), we must deduct one period (one month) from the annuity due term.
Thus, the fund will be depleted in 20 years and 10 months.
Section 3.10 Exercises
- Karina wants to accumulate $52,500 for her condominium down payment. She plans to make deposits of $1,330 at the beginning of every month into her savings account, which earns interest at 6.61% compounded monthly. a) How many deposits will Karina have to make to achieve her goal? b) How long will it take? Give the time in terms of years and months.
Show/Hide Answer
a) N = 36 deposits
b) t = 3 years and 0 months
- BoardWalk Corporation aims to save a total of $641,000 over the coming years. They plan to start with an initial deposit of $176,800 and then make deposits of $5,200 at the end of each month. (a) Determine the number of additional monthly deposits and (b) the total time required for BoardWalk Corporation to accumulate $641,000, considering an interest rate of 6.37% compounded semi-annually. Give the time in years and months.
Show/Hide Answer
a) N = 64 payments
b) t = 5 years and 4 months
- Alo has saved $2,500,000 in his retirement fund, which earns an annual interest rate of 1.5% compounded daily. He intends to withdraw $10,000 at the beginning of every month. a) Calculate the total number of withdrawals Alo will make. b) Determine the duration for which Alo's retirement fund will sustain these monthly withdrawals. Give the time in years and months.
Show/Hide Answer
a) N = 300 withdrawals
b) t = 25 years

