Annuities
3.1 Introduction to Annuities
A. Definition of Annuity
An annuity is defined as a series of periodic payments, usually in equal size, made at regular time intervals. In annuities, the interest that is charged on money is usually compound interest. Mortgages and car loans or leases are examples of annuities. Typical payment intervals of annuities are monthly, quarterly, semi-annually, and annually, as summarized in Table 3.1.1.
Table 3.1.1 Number of payments per year for different payment intervals
| Payment Interval | Length of Payment Period | Number of Payments per Year (P/Y) |
| Annually | Every 12 months (1 year) | 1 |
| Semi-annually | Every 6 months | 2 |
| Quarterly | Every 3 months | 4 |
| Monthly | Every month | 12 |
| Bi-weekly | Every two weeks | 26 |
| Weekly | Every week | 52 |
Payments can be made at the beginning or end of payment intervals. For example, for monthly payments, the payment can be made on the first day of a month or the last day of a month.

Unlike compound interest problems where [asciimath]N[/asciimath] represents the total number of compounding periods in the loan or investment term, in annuities, [asciimath]N[/asciimath] represents the total number of payments in the term and can be obtained by
[asciimath]N=P//Y*t[/asciimath] Formula 3.1a
where [asciimath]P//Y[/asciimath] is the number of periodic payments in a year, and [asciimath]t[/asciimath] is the time period of the annuity in years.
When solving time-value-of-money problems, it is crucial first to identify the type of problem you are dealing with. Compound interest problems typically involve a single lump sum or irregular deposits or withdrawals occurring over time. In contrast, annuity problems involve a series of equal cash flows, either payments or withdrawals, that are made or received at regular intervals over a specified period.
To differentiate between compound interest and annuity problems, pay attention to certain keywords. Phrases like "every" or "each," or time-related adverbs such as "weekly" and "monthly," often indicate that the problem is related to annuities, involving regular, equal payments or withdrawals.
For each given scenario, determine the number of payments per Year (P/Y), term in years (t), and the number of payments in the term (N).
a) You deposit $200 at the end of every 3 months for 5 years.
b) Payments of $1050 made at the end of each month for 4 years and 5 months.
c) Monthly payment of $150 for 4.5 years.
Show/Hide Solution
We first look for a keyword that indicates that the given payment is periodic, and thus the problem is indeed an annuity. In each example, the keyword is boldfaced. Once the number of payments in a year (P/Y) and the term duration (t) are determined, we use Formula 3.1a to compute the number of payments in the term (N).
a) You deposit $200 at the end of every 3 months for 5 years.
- Number of payments in a year: Every 3 months so [asciimath]P//Y = 4[/asciimath]
- Term: [asciimath]t=5[/asciimath] years
- Number of payments in the term: [asciimath]N=4(5)=20[/asciimath]
b) Payments of $1050 made at the end of each month for 4 years and 5 months.
- Number of payments in a year: Each month so [asciimath]P//Y = 12[/asciimath]
- Term: [asciimath]t=4\ "years"+5\ "months"=[/asciimath] [asciimath]4\ "years"+5/12\ "years"=[/asciimath][asciimath]4 5/12\ "years"[/asciimath]
- Number of payments in the term: [asciimath]N=12(4 5/12)=53[/asciimath]
c) Weekly payment of $150 for 4.5 years.
- Number of payments in a year: Weekly so [asciimath]P//Y = 52[/asciimath]
- Term: [asciimath]t=4.5[/asciimath] years
- Number of payments in the term: [asciimath]N=52(4.5)=234[/asciimath]
B. Components of Annuities
Each annuity problem has two pieces of information that you need to pay attention to:
- Information about the periodic payments
- Size of the periodic payment (PMT)
- Number of payments per year (P/Y)
- The timing of payments (whether it is at the beginning or the end of the payment period)
- Information about the interest charged
- Nominal interest rate (I/Y)
- The number of interest compounding periods per year (C/Y)
For example, in the case of "payments of $200 are made at the end of every quarter for 3 years into a savings account earning 6% compounded semi-annually", the first part of the sentence provides information about the size, frequency, and timing of the payments, and the second part of the sentence gives information regarding the interest. Note that the phrase related to the interest is identical to compound interest problems.

C. Types of Annuities
Annuities can be classified in various ways, with a common approach based on the timing of payments in annuities and the relationship between frequencies of payments and interest-compounding periods. In this book, our focus is on immediate-start annuities that have predetermined maturity dates, aligning with these common classifications. We will not delve into deferred annuities, which begin payments at a later date, nor will we cover perpetuities, which do not have a set endpoint. Our discussion aims to provide a clear understanding of the most typical annuity structures encountered in financial planning:
- Classified in terms of the timing of payments whether it is at the beginning or the end of the payment period.
- Ordinary Annuity (end)
- Annuity due (beginning)
- Classified in terms of the frequencies of payments and interest-compounding periods
- Simple Annuity (equal frequencies)
- General Annuity (unequal frequencies)
The combination of those four classes gives four different types of annuities, as illustrated in Figure 3.1.1.
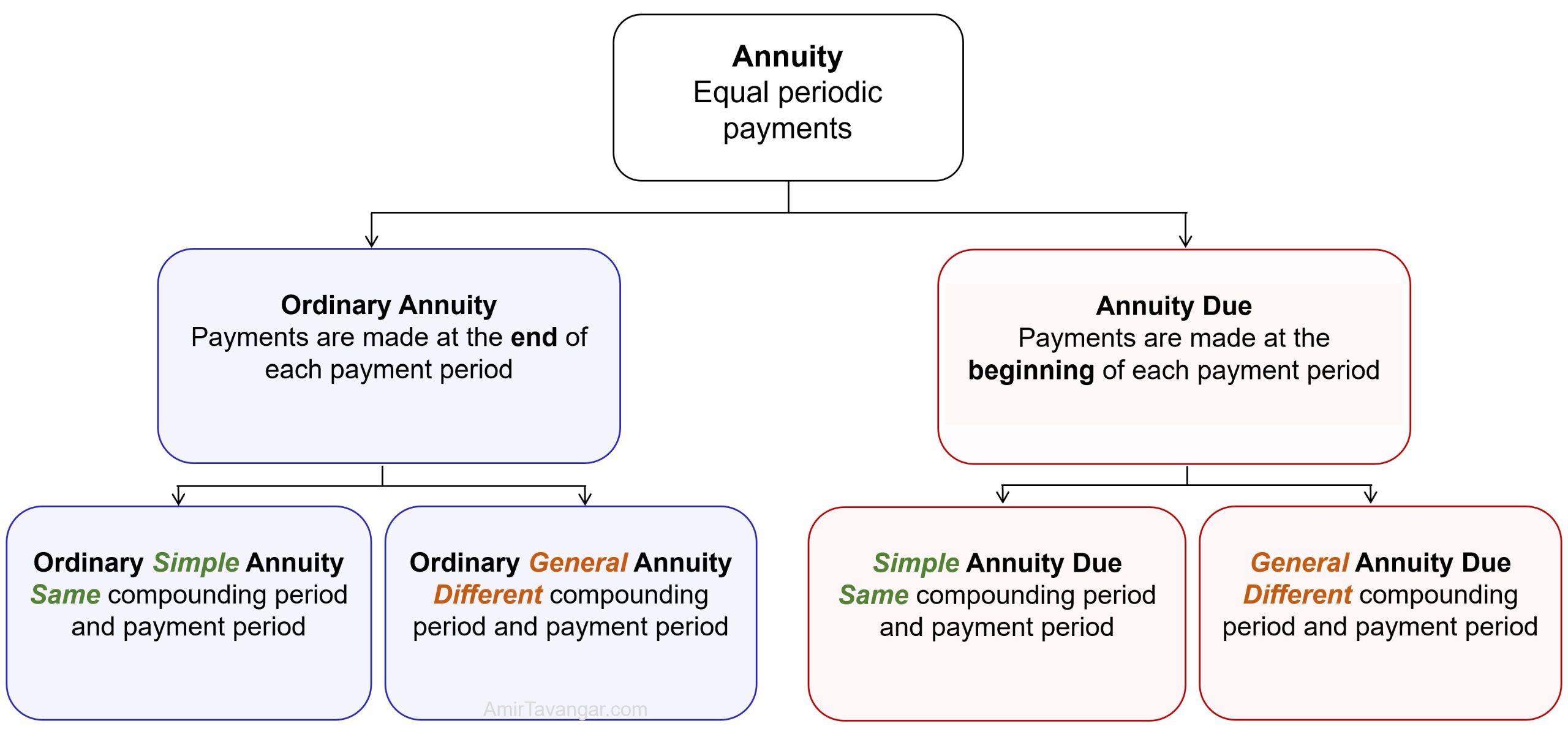
Figure 3.1.1 Types of Annuities
In an Ordinary Simple Annuity, the payment period and the interest compounding period are the same ([asciimath]P//Y = C//Y[/asciimath]), and the payments are made at the end of the payment period.

In an Ordinary General Annuity, the payment period and the interest compounding period are NOT the same ([asciimath]P//Y != C//Y[/asciimath]) and the payments are made at the end of the payment period.


In a General Annuity Due, the payment period and the interest compounding period are NOT the same ([asciimath]P//Y != C//Y[/asciimath]) and the payments are made at the beginning of the payment period.

Identify the type of Annuities.
a) Payments of $540 at the end of every year for 6 years at 4.76% compounded annually.
b) Payments of $85 at the end of every month for 6 years at 8.15% compounded annually.
c) Payments of $540 at the beginning of every 3 months for 4.5 years at 5 % compounded quarterly.
d) Payments of $1200 at the beginning of every 6 months for 8 years at 3.40% compounded monthly.
Show/Hide Solution
Since [asciimath]P//Y=C//Y[/asciimath], the annuity is simple. Also, the payments are made at the END of the payment period, so the annuity is ordinary. Putting them together, the annuity is an Ordinary Simple Annuity.
Since [asciimath]P//Y!=C//Y[/asciimath], the annuity is general. Also, the payments are made at the END of the payment period, so the annuity is ordinary. Putting them together, the annuity is an Ordinary General Annuity.
Since [asciimath]P//Y=C//Y[/asciimath], the annuity is simple. Also, the payments are made at the BEGINNING of the payment period, so the annuity is an annuity due. Putting them together, the annuity is a Simple Annuity Due.
d) Payments of $1200 at the [asciimath]obrace("beginning")^("Due")[/asciimath] of every [asciimath]obrace("6 months")^(P//Y=2)[/asciimath] for 8 years at 3.40% compounded [asciimath]obrace("monthly")^(C//Y=12)[/asciimath].
Since [asciimath]P//Y!=C//Y[/asciimath], the annuity is general. Also, the payments are made at the BEGINNING of the payment period, so the annuity is an annuity due. Putting them together, the annuity is a General Annuity Due.
Try an Example
Section 3.1 Exercises
- Identify the type of annuity: Payments of $300 are made at the beginning of every six months for 9 years at 8% compounded semi-annually.
Show/Hide Answer
Simple Annuity due - Identify the type of annuity: Payments of $670 are made at the end of every year for 5 years at 3.7% compounded monthly.
Show/Hide Answer
Ordinary General annuity - Identify the type of annuity: Payments of $510 are made at the beginning of every year for 6 years at 2.9% compounded quarterly.
Show/Hide Answer
General Annuity due

