Compound Interest
2.3 Present Value: Calculator Approach
To find out the initial amount of money required to achieve a certain future value, we calculate the present value (PV). This amount represents the initial sum of money that, after accruing interest over time, will reach the desired future amount. The present value can also be considered the equivalent value of a given sum of money at an earlier point in time. When using a financial calculator to find the PV, follow the steps outlined in Section 2.2, but in this case, PV is the variable we compute.
The method of calculating the present value of a given future value is called discounting. Thus, the present value is sometimes referred to as the discounted value, and the amount of interest calculated for such cases is called the compound discount. The compound discount is obtained the same way the compound interest is computed using Formula 2.3.
Calculate the present value of $4320 that is due in 5 years and 9 months given the interest rate is 3.45% compounded semi-annually.
Watch Video
Show/Hide Solution
Given information:
- Future value (inflow): [asciimath]FV = $4320[/asciimath]
- Nominal interest rate: [asciimath]I//Y = 3.45%[/asciimath]
- Interest is compounded monthly so [asciimath]P//Y=C//Y = 2[/asciimath]
- Compound Term: [asciimath]t =[/asciimath] 5 years + 8 months [asciimath]= 5+9/12=5.75[/asciimath] years
- Number of compounding periods in the term: [asciimath]N =C//Y*t=2 (5.75) = 11.5[/asciimath]
[asciimath]PV=?[/asciimath]
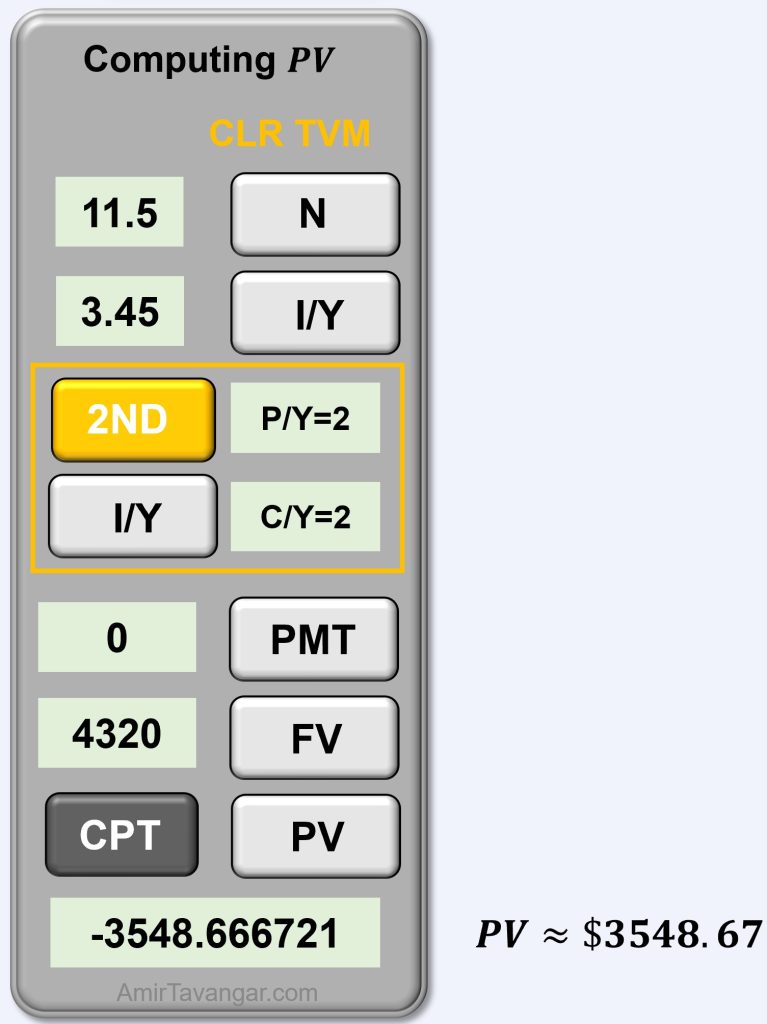
Therefore, the present value is $3548.67.
Try an Example
Section 2.3 Exercises
- Wyatt would like to accumulate $197,100 for his retirement in 16 years. If his local bank promises him 4.16% compounded quarterly, how much he should invest today?
Show/Hide Answer
PV = $101,651.32
- Find the amount paid for an investment that will mature to $171,000 in 6 years and 2 months at the interest rate of 3.04% compounded quarterly.
Show/Hide Answer
PV = $141,869.22
- Compute the present value of $132,300 that is invested for 8 years and 6 months at 4.36% compounded monthly.
Show/Hide Answer
PV = $91,390.70

