9.4 Variation of Pressure with Depth in a Fluid
Learning Objectives
By the end of this section, you will be able to:
- Define pressure in terms of weight.
- Explain the variation of pressure with depth in a fluid.
- Calculate density given pressure and altitude.
If your ears have ever popped on a plane flight or ached during a deep dive in a swimming pool, you have experienced the effect of depth on pressure in a fluid. At the Earth’s surface, the air pressure exerted on you is a result of the weight of air above you. This pressure is reduced as you climb up in altitude and the weight of air above you decreases. Under water, the pressure exerted on you increases with increasing depth. In this case, the pressure being exerted upon you is a result of both the weight of water above you and that of the atmosphere above you. You may notice an air pressure change on an elevator ride that transports you many stories, but you need only dive a meter or so below the surface of a pool to feel a pressure increase. The difference is that water is much denser than air, about 775 times as dense.
Consider the container in Figure 9.8. Its bottom supports the weight of the fluid in it. Let us calculate the pressure exerted on the bottom by the weight of the fluid. That pressure is the weight of the fluid [latex]\text{mg}[/latex] divided by the area [latex]A[/latex] supporting it (the area of the bottom of the container):
[latex]P = \frac{\text{mg}}{A} .[/latex]
We can find the mass of the fluid from its volume and density:
[latex]m = ρV .[/latex]
The volume of the fluid [latex]V[/latex] is related to the dimensions of the container. It is
[latex]V = \text{Ah} ,[/latex]
where [latex]A[/latex] is the cross-sectional area and [latex]h[/latex] is the depth. Combining the last two equations gives
[latex]m = \rho \text{Ah} .[/latex]
If we enter this into the expression for pressure, we obtain
[latex]P = \frac{\left(\rho \text{Ah}\right) g}{A} .[/latex]
The area cancels, and rearranging the variables yields
[latex]P = hρg .[/latex]
This value is the pressure due to the weight of a fluid. The equation has general validity beyond the special conditions under which it is derived here. Even if the container were not there, the surrounding fluid would still exert this pressure, keeping the fluid static. Thus the equation [latex]P = hρg[/latex] represents the pressure due to the weight of any fluid of average density [latex]\rho[/latex] at any depth [latex]h[/latex] below its surface. For liquids, which are nearly incompressible, this equation holds to great depths. For gases, which are quite compressible, one can apply this equation as long as the density changes are small over the depth considered. Example 9.4 illustrates this situation.
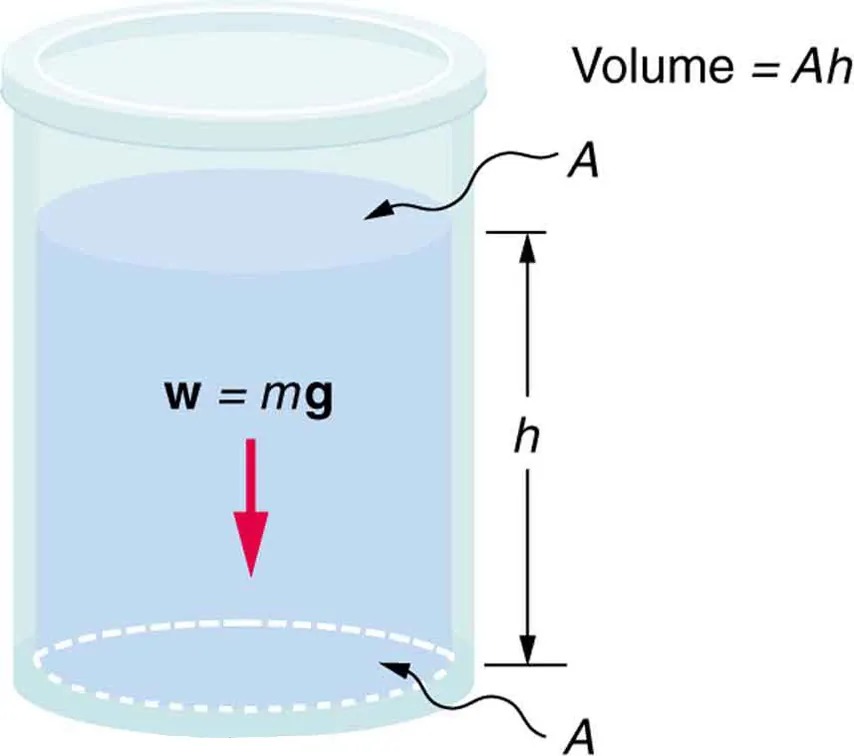
Figure 9.8 The bottom of this container supports the entire weight of the fluid in it. The vertical sides cannot exert an upward force on the fluid (since it cannot withstand a shearing force), and so the bottom must support it all. Image from OpenStax College Physics 2e, CC-BY 4.0
Image Description
The image is a diagram of a cylindrical container filled with a liquid. The following elements are indicated:
- The cylindrical container is shown with a light blue liquid inside.
- There is a downward pointing red arrow labeled “w = mg”, representing the weight of the liquid.
- The top and bottom surfaces of the container are labeled as “A”, representing the area of these surfaces.
- The height of the liquid is labeled “h”.
- The right side of the image states “Volume = Ah”, indicating the volume of the liquid inside the cylinder is calculated by multiplying the area of the base by the height.
Example 9.3
Calculating the Average Pressure and Force Exerted: What Force Must a Dam Withstand?
In Example 9.1, we calculated the mass of water in a large reservoir. We will now consider the pressure and force acting on the dam retaining water. (See Figure 9.9.) The dam is 500 m wide, and the water is 80.0 m deep at the dam. (a) What is the average pressure on the dam due to the water? (b) Calculate the force exerted against the dam and compare it with the weight of water in the dam (previously found to be [latex]1.96 \times 10^{13} \text{N}[/latex]).
Strategy for (a)
The average pressure [latex]\bar{P}[/latex]
due to the weight of the water is the pressure at the average depth [latex]\bar{h}[/latex]
of 40.0 m, since pressure increases linearly with depth.
Solution for (a)
The average pressure due to the weight of a fluid is
[latex]\bar{P} = \bar{h} ρg .[/latex]
Entering the density of water from Table 9.1 and taking [latex]\bar{h}[/latex] to be the average depth of 40.0 m, we obtain
[latex]\begin{eqnarray*}\bar{P} & = & \left(\right. \text{40}.\text{0 m} \left.\right) \left(\text{10}^{3} \frac{\text{kg}}{\text{m}^{3}}\right) \left(9.80 \frac{\text{m}}{\text{s}^{2}}\right) \\ & = & 3.92 \times \text{10}^{5} \frac{\text{N}}{\text{m}^{2}} = \text{392 kPa}.\end{eqnarray*}[/latex]
Strategy for (b)
The force exerted on the dam by the water is the average pressure times the area of contact:
[latex]F = \bar{P} A .[/latex]
Solution for (b)
We have already found the value for [latex]\bar{P}[/latex]. The area of the dam is [latex]A = \text{80}.\text{0 m} \times \text{500 m} = 4.00 \times \text{10}^{4} \text{m}^{2}[/latex], so that
[latex]\begin{eqnarray*}F & = & \left(\right. 3.92 \times \text{10}^{5} \text{N}/\text{m}^{2} \left.\right) \left(\right. 4.00 \times \text{10}^{4} \text{m}^{2} \left.\right) \\ & = & 1.57 \times \text{10}^{\text{10}} \text{N}.\end{eqnarray*}[/latex]
Discussion
Although this force seems large, it is small compared with the [latex]1.96 \times \text{10}^{\text{13}} \text{N}[/latex] weight of the water in the reservoir—in fact, it is only
[latex]0.0800%[/latex] of the weight. Note that the pressure found in part (a) is completely independent of the width and length of the lake—it depends only on its average depth at the dam. Thus the force depends only on the water’s average depth and the dimensions of the dam, not on the horizontal extent of the reservoir. In the diagram, the thickness of the dam increases with depth to balance the increasing force due to the increasing pressure.
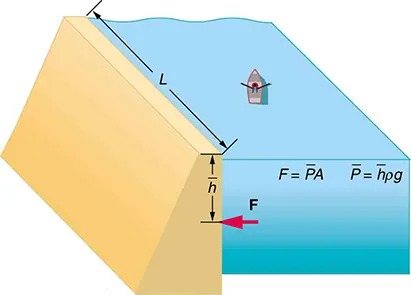
Figure 9.9 The dam must withstand the force exerted against it by the water it retains. This force is small compared with the weight of the water behind the dam. Image from OpenStax College Physics 2e, CC-BY 4.0
Image Description
The image depicts a diagram of a dam and a body of water. On the left side, there is a triangular cross-section of a dam shown in yellow, which is slanted towards the right. The body of water is shown in blue against the right side of the dam.
The image includes the following labeled elements:
- A line labeled “L” showing the length of the water against the dam.
- A vertical line labeled “h” indicating the depth of water from the surface to the base of the dam.
- An arrow marked “F” pointing horizontally from the water towards the dam, indicating the force exerted by the water on the dam.
The image also contains two equations:
- F = PA, representing the force as the product of pressure and area.
- P = hpg, indicating pressure as the product of height, density of the fluid (p), and acceleration due to gravity (g).
A small boat is depicted floating on the surface of the water, slightly to the right of the dam structure.
Atmospheric pressure is another example of pressure due to the weight of a fluid, in this case due to the weight of air above a given height. The atmospheric pressure at the Earth’s surface varies a little due to the large-scale flow of the atmosphere induced by the Earth’s rotation (this creates weather “highs” and “lows”). However, the average pressure at sea level is given by the standard atmospheric pressure [latex]P_{\text{atm}}[/latex], measured to be
[latex]{\small\text{1 atmosphere }(\text{atm}) = P_{\text{atm}} = 1.01 \times \text{10}^{5} \text{N}/\text{m}^{2} = \text{101 kPa} .}[/latex]
This relationship means that, on average, at sea level, a column of air above [latex]1.00 \text{m}^{2}[/latex] of the Earth’s surface has a weight of [latex]1.01 \times \text{10}^{5} \text{N}[/latex], equivalent to [latex]\text{1 atm}[/latex]. (See Figure 9.10.)

Figure 9.10 Atmospheric pressure at sea level averages [latex]1 . \text{01} \times \text{10}^{5} \text{Pa}[/latex] (equivalent to 1 atm), since the column of air over this [latex]1 \text{m}^{2}[/latex], extending to the top of the atmosphere, weighs [latex]1 . \text{01} \times \text{10}^{5} \text{ N}[/latex]. Image from OpenStax College Physics 2e, CC-BY 4.0
Image Description
The image depicts a diagram illustrating atmospheric pressure. On the left side, there is a vertical stack of red lines, representing the weight of the atmosphere over a specific area. Below this stack is a 3D box drawn on the ground, labeled as covering an area of “1 m2“. An arrow points from these lines to an equation, indicating that the weight (w) is equal to “1.01 × 105 N” (Newtons).
On the right side of the image, there is a tree and a cloud. The presence of these natural elements suggests that the concept relates to the point that atmospheric pressure is exerted over all surfaces, including trees and the ground.
Example 9.4
Calculating Average Density: How Dense Is the Air?
Calculate the average density of the atmosphere, given that it extends to an altitude of 120 km. Compare this density with that of air listed in Table 9.1.
Strategy
If we solve [latex]P = hρg[/latex] for density, we see that
[latex]\bar{\rho} = \frac{P}{\text{hg}} .[/latex]
We then take [latex]P[/latex] to be atmospheric pressure, [latex]h[/latex] is given, and [latex]g[/latex] is known, and so we can use this to calculate [latex]\bar{\rho}[/latex].
Solution
Entering known values into the expression for [latex]\bar{\rho}[/latex] yields
[latex]\bar{\rho} = \frac{1 . \text{01} \times \text{10}^{5} \text{N}/\text{m}^{2}}{\left(\right. \text{120} \times \text{10}^{3} \text{m} \left.\right) \left(\right. 9 . \text{80} \text{m}/\text{s}^{2} \left.\right)} = 8 . \text{59} \times \text{10}^{- 2} \text{kg}/\text{m}^{3} .[/latex]
Discussion
This result is the average density of air between the Earth’s surface and the top of the Earth’s atmosphere, which essentially ends at 120 km. The density of air at sea level is given in Table 9.1 as [latex]1 . \text{29} \text{kg}/\text{m}^{3}[/latex] —about 15 times its average value. Because air is so compressible, its density has its highest value near the Earth’s surface and declines rapidly with altitude.
Example 9.5
Calculating Depth Below the Surface of Water: What Depth of Water Creates the Same Pressure as the Entire Atmosphere?
Calculate the depth below the surface of water at which the pressure due to the weight of the water equals 1.00 atm.
Strategy
We begin by solving the equation [latex]P = hρg[/latex] for depth [latex]h[/latex]:
[latex]h = \frac{P}{ρg} .[/latex]
Then we take [latex]P[/latex] to be 1.00 atm and [latex]\rho[/latex] to be the density of the water that creates the pressure.
Solution
Entering the known values into the expression for [latex]h[/latex] gives
[latex]h = \frac{1 . \text{01} \times \text{10}^{5} \text{N}/\text{m}^{2}}{\left(\right. 1 . \text{00} \times \text{10}^{3} \text{kg}/\text{m}^{3} \left.\right) \left(\right. 9 . \text{80} \text{m}/\text{s}^{2} \left.\right)} = \text{10} . 3 \text{m} .[/latex]
Discussion
Just 10.3 m of water creates the same pressure as 120 km of air. Since water is nearly incompressible, we can neglect any change in its density over this depth.
What do you suppose is the total pressure at a depth of 10.3 m in a swimming pool? Does the atmospheric pressure on the water’s surface affect the pressure below? The answer is yes. This seems only logical, since both the water’s weight and the atmosphere’s weight must be supported. So the total pressure at a depth of 10.3 m is 2 atm—half from the water above and half from the air above. We shall see in 9.5 Pascal’s Principle that fluid pressures always add in this way.

