"

Problems & Exercises

Problems & Exercises

4.3 Newton’s Second Law of Motion: Concept of a System

You may assume data taken from illustrations is accurate to three digits.

  1. A 63.0-kg sprinter starts a race with an acceleration of [latex]4 . \text{20 m} /\text{s}^{2}[/latex]. What is the net external force on him?
  2. If the sprinter from the previous problem accelerates at that rate for 20 m, and then maintains that velocity for the remainder of the 100-m dash, what will be his time for the race?
  3. A cleaner pushes a 4.50-kg laundry cart in such a way that the net external force on it is 60.0 N. Calculate the magnitude of its acceleration.
  4. Since astronauts in orbit are apparently weightless, a clever method of measuring their masses is needed to monitor their mass gains or losses to adjust diets. One way to do this is to exert a known force on an astronaut and measure the acceleration produced. Suppose a net external force of 50.0 N is exerted and the astronaut’s acceleration is measured to be [latex]0 . \text{893 m}/\text{s}^{2}[/latex]. (a) Calculate her mass. (b) By exerting a force on the astronaut, the vehicle in which they orbit experiences an equal and opposite force. Discuss how this would affect the measurement of the astronaut’s acceleration. Propose a method in which recoil of the vehicle is avoided.
  5. In Figure 4.7, the net external force on the 24-kg mower is stated to be 51 N. If the force of friction opposing the motion is 24 N, what force [latex]F[/latex] (in newtons) is the person exerting on the mower? Suppose the mower is moving at 1.5 m/s when the force [latex]F[/latex] is removed. How far will the mower go before stopping?
  6. The same rocket sled drawn in Figure 4.36 is decelerated at a rate of [latex]1 \text{96 m}/\text{s}^{2}[/latex]. What force is necessary to produce this deceleration? Assume that the rockets are off. The mass of the system is 2100 kg.
A sled is shown with four rockets. Friction force is represented by an arrow labeled as vector f pointing toward the left on the sled. Weight of the sled is represented by an arrow labeled as vector W, shown pointing downward, and normal force is represented by an arrow labeled as vector N having the same length as W acting upward on the sled.

Figure 4.36 Image from OpenStax College Physics 2e, CC-BY 4.0

Image Description

The image shows a side view of a streamlined, futuristic train-like vehicle traveling along a track. The vehicle appears aerodynamic, with smooth curves and a sleek design. It has a large tail fin, suggesting high speed. A person is visible inside the cockpit of the vehicle.

There are several arrows indicating forces acting on the vehicle:

– A red arrow pointing to the right is labeled “f”, representing the forward driving force.
– Two arrows pointing downward towards the track are labeled “N” and “w”. “N” likely represents the normal force exerted by the track, and “w” represents the weight of the vehicle.
– A wispy, smoky trail is shown behind the vehicle, indicating movement or speed.

Overall, the image presents a dynamic depiction of motion and forces acting on the vehicle as it moves along the track.

  1. (a) If the rocket sled shown in Figure 4.37 starts with only one rocket burning, what is the magnitude of its acceleration? Assume that the mass of the system is 2100 kg, the thrust T is [latex]2.59 \times 10^{4}[/latex] N, and the force of friction opposing the motion is known to be 650 N. (b) Why is the acceleration not one-fourth of what it is with all rockets burning?
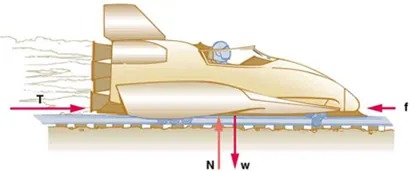
A sled is shown with thrust represented by a vector T pushing the sled toward the right. Friction force is represented by an arrow labeled as vector f pointing toward the left on the sled. The weight of the sled is represented by an arrow labeled as vector W, shown pointing downward, and the normal force is represented by an arrow labeled as vector N having the same length as W acting upward on the sled.

Figure 4.37 Image from OpenStax College Physics 2e, CC-BY 4.0

Image Description

The image shows a schematic side view of a streamlined vehicle, resembling a bobsled, moving along a track. The vehicle has a sleek design and is shown with indicators pointing to various forces acting upon it. These forces are represented by arrows with labels:

– An arrow labeled “T” points to the left, indicating thrust or a propelling force.
– An arrow labeled “f” points to the right, indicating friction acting against the motion of the vehicle.
– Two arrows labeled “N” and “w” point downward and upward respectively, indicating the normal force and the weight of the vehicle.

The vehicle is depicted in motion, with lines suggesting speed and airflow over the surface.

  1. What is the deceleration of the rocket sled if it comes to rest in 1.1 s from a speed of 1000 km/h? (Such deceleration caused one test subject to black out and have temporary blindness.)
    1. What is the system of interest if the acceleration of the child in the wagon is to be calculated?
    2. Draw a free-body diagram, including all forces acting on the system.
    3. Calculate the acceleration.
    4. What would the acceleration be if friction were 15.0 N?Suppose two children push horizontally, but in exactly opposite directions, on a third child in a wagon. The first child exerts a force of 75.0 N, the second a force of 90.0 N, friction is 12.0 N, and the mass of the third child plus wagon is 23.0 kg.
  3. A powerful motorcycle can produce an acceleration of [latex]3.50 \text{ m}/\text{s}^{2}[/latex] while traveling at 90.0 km/h. At that speed the forces resisting motion, including friction and air resistance, total 400 N. (Air resistance is analogous to air friction. It always opposes the motion of an object.) What is the magnitude of the force the motorcycle exerts backward on the ground to produce its acceleration if the mass of the motorcycle with rider is 245 kg?
  4. The rocket sled shown in Figure 4.38 accelerates at a rate of [latex]49.0 \text{ m}/\text{s}^{2}[/latex]. Its passenger has a mass of 75.0 kg. (a) Calculate the horizontal component of the force the seat exerts against his body. Compare this with his weight by using a ratio. (b) Calculate the direction and magnitude of the total force the seat exerts against his body.
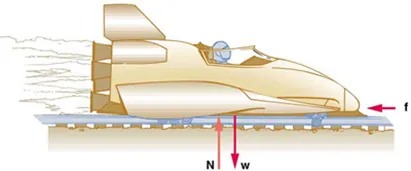
A sled is shown with four rockets. Friction force is represented by an arrow labeled as vector f pointing toward the left on the sled. The weight of the sled is represented by an arrow labeled as vector W, shown pointing downward, and the normal force is represented by an arrow labeled as vector N having the same length as W acting upward on the sled.

Figure 4.38 Image from OpenStax College Physics 2e, CC-BY 4.0

Image Description

The image illustrates a streamlined, futuristic vehicle that resembles a high-speed train or a rocket-powered car. The vehicle is depicted from the side and is moving to the right. It has a sleek, aerodynamic shape with a pointed nose and fin-like structures at the rear. A trail of exhaust or vapor is shown behind the vehicle, indicating high speed.

A person is seated inside the vehicle, positioned near the front. The vehicle is on a set of rails or a track, suggesting it’s designed for guided travel. Below the vehicle, three arrows indicate forces acting upon it:

1. A red arrow pointing to the right labeled “f” represents the forward force or thrust pushing the vehicle forward.
2. A downward red arrow labeled “w” represents the weight of the vehicle.
3. An upward red arrow labeled “N” represents the normal force exerted by the track on the vehicle.

The visual suggests the dynamics of motion and the forces involved in keeping the vehicle on its track.

  1. Repeat the previous problem for the situation in which the rocket sled decelerates at a rate of [latex]2 \text{01 m}/\text{s}^{2}[/latex]. In this problem, the forces are exerted by the seat and restraining belts.
  2. The weight of an astronaut plus their space suit on the Moon is only 250 N. How much do they weigh on Earth? What is the mass on the Moon? On Earth?
  3. Suppose the mass of a fully loaded module in which astronauts take off from the Moon is 10,000 kg. The thrust of its engines is 30,000 N. (a) Calculate its the magnitude of acceleration in a vertical takeoff from the Moon. (b) Could it lift off from Earth? If not, why not? If it could, calculate the magnitude of its acceleration.

4.4 Newton’s Third Law of Motion: Symmetry in Forces

  1. What net external force is exerted on a 1100-kg artillery shell fired from a battleship if the shell is accelerated at [latex]2 . \text{40} \times \text{10}^{4} \text{ m}/\text{s}^{2}[/latex]? What is the magnitude of the force exerted on the ship by the artillery shell?
  2. A rugby player is being pushed backward by an opposing player who is exerting a force of 800 N on him. The mass of the losing player plus equipment is 90.0 kg, and he is accelerating at [latex]1 . \text{20} \text{ m}/\text{s}^{2}[/latex] backward. (a) What is the force of friction between the losing player’s feet and the grass? (b) What force does the winning player exert on the ground to move forward if his mass plus equipment is 110 kg? (c) Draw a sketch of the situation showing the system of interest used to solve each part. For this situation, draw a free-body diagram and write the net force equation.

4.5 Normal, Tension, and Other Examples of Forces

  1. Two teams of nine members each engage in a tug of war. Each of the first team’s members has an average mass of 68 kg and exerts an average force of 1350 N horizontally. Each of the second team’s members has an average mass of 73 kg and exerts an average force of 1365 N horizontally. (a) What is magnitude of the acceleration of the two teams? (b) What is the tension in the section of rope between the teams?
  2. What force does a trampoline have to apply to a 45.0-kg gymnast to accelerate her straight up at [latex]7 . \text{50 m}/\text{s}^{2}[/latex]? Note that the answer is independent of the velocity of the gymnast—she can be moving either up or down, or be stationary.
  3. (a) Calculate the tension in a vertical strand of spider web if a spider of mass [latex]8 . \text{00} \times \text{10}^{- 5} \text{ kg}[/latex] hangs motionless on it. (b) Calculate the tension in a horizontal strand of spider web if the same spider sits motionless in the middle of it much like the tightrope walker in Figure 4.16. The strand sags at an angle of [latex]\text{12}º[/latex] below the horizontal. Compare this with the tension in the vertical strand (find their ratio).
  4. Suppose a 60.0-kg gymnast climbs a rope. (a) What is the tension in the rope if they climb at a constant speed? (b) What is the tension in the rope if they accelerate upward at a rate of [latex]1 . \text{50 m}/\text{s}^{2}[/latex]?
  5. Show that, as stated in the text, a force [latex]\textbf{F}_{\bot}[/latex] exerted on a flexible medium at its center and perpendicular to its length (such as on the tightrope wire in Figure 4.16) gives rise to a tension of magnitude
  6. [latex]T = \frac{F_{\bot}}{2 \text{sin} \left(\right. \theta \left.\right)}[/latex].
  7. Consider the baby being weighed in Figure 4.39. (a) What is the mass of the child and basket if a scale reading of 55 N is observed? (b) What is the tension [latex]T_{1}[/latex] in the cord attaching the baby to the scale? (c) What is the tension [latex]T_{2}[/latex] in the cord attaching the scale to the ceiling, if the scale has a mass of 0.500 kg? (d) Draw a sketch of the situation indicating the system of interest used to solve each part. The masses of the cords are negligible.
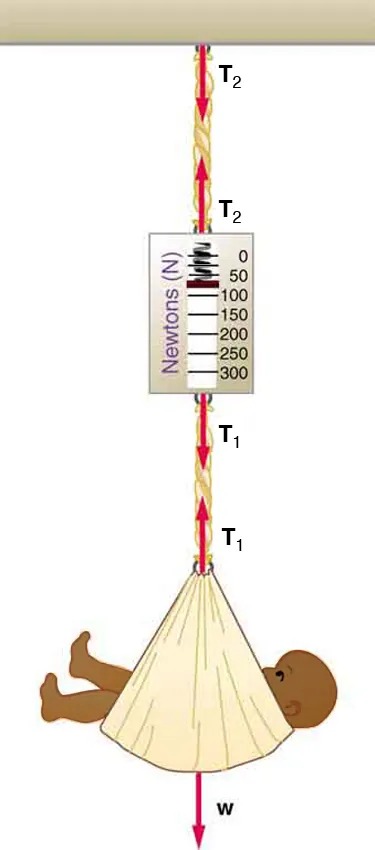
A vertical spring scale measuring the weight of a baby is shown. The scale is hung from the ceiling by a cord. The weight W of the baby is shown by a vector arrow acting downward and tension T sub one acting in the cord is shown by an arrow upward. The tension in the cord T sub two attached to the ceiling is represented by an arrow upward from the spring scale and downward from the ceiling.

Figure 4.39 A baby is weighed using a spring scale. Image from OpenStax College Physics 2e, CC-BY 4.0

Image Description

The image shows a diagram depicting a baby lying in a hammock-like cloth suspended from a ceiling. The setup illustrates forces in physics, specifically focusing on tension. Here’s a detailed description:

– A small child, depicted as an illustration, is lying in a triangular hammock or cloth sling.
– The cloth is connected to a rope, which is tied above to a point on the ceiling.
– The rope is divided into two sections, labeled as T1 and T2, indicating the tension in the rope.
– These tension forces (T1 and T2) are visualized with red arrows pointing upwards along the rope, indicating the direction of the tension forces.
– Between the segments of the rope, there is a spring scale showing the force in Newtons, acting as a measuring device. The scale shows measurements ranging from 0 to 300 Newtons, marked in increments of 50.
– The reading shown on the scale is around 150 Newtons.
– Below the child, a downward arrow marked “w” indicates the weight of the child, representing the force of gravity acting on the child’s mass.

This setup is commonly used to illustrate concepts of tension and equilibrium in physics, showing how tension varies along a rope when supporting a weight.

4.6 Problem-Solving Strategies

  1. A [latex]5 . \text{00} \times \text{10}^{5} -\text{kg}[/latex] rocket is accelerating straight up. Its engines produce [latex]1 . \text{250} \times \text{10}^{7} \text{ N}[/latex] of thrust, and air resistance is [latex]4 . \text{50} \times \text{10}^{6} \text{ N}[/latex]. What is the rocket’s acceleration? Explicitly show how you follow the steps in the Problem-Solving Strategy for Newton’s laws of motion.
  2. The wheels of a midsize car exert a force of 2100 N backward on the road to accelerate the car in the forward direction. If the force of friction including air resistance is 250 N and the acceleration of the car is [latex]1 . \text{80 m}/\text{s}^{2}[/latex], what is the mass of the car plus its occupants? Explicitly show how you follow the steps in the Problem-Solving Strategy for Newton’s laws of motion. For this situation, draw a free-body diagram and write the net force equation.
  3. Calculate the force a 70.0-kg high jumper must exert on the ground to produce an upward acceleration 4.00 times the acceleration due to gravity. Explicitly show how you follow the steps in the Problem-Solving Strategy for Newton’s laws of motion.
  4. When landing after a spectacular somersault, a 40.0-kg gymnast decelerates by pushing straight down on the mat. Calculate the force she must exert if her deceleration is 7.00 times the acceleration due to gravity. Explicitly show how you follow the steps in the Problem-Solving Strategy for Newton’s laws of motion.
  5. A freight train consists of two [latex]8.00 \times 10^{4} -\text{kg}[/latex] engines and 45 cars with average masses of [latex]5.50 \times 10^{4} \text{kg}[/latex]. (a) What force must each engine exert backward on the track to accelerate the train at a rate of [latex]5.00 \times \text{10}^{–\text{2}} \text{ m}/\text{s}^{2}[/latex] if the force of friction is [latex]7 . \text{50} \times \text{10}^{5} \text{ N}[/latex], assuming the engines exert identical forces? This is not a large frictional force for such a massive system. Rolling friction for trains is small, and consequently trains are very energy-efficient transportation systems. (b) What is the force in the coupling between the 37th and 38th cars (this is the force each exerts on the other), assuming all cars have the same mass and that friction is evenly distributed among all of the cars and engines?
  6. Commercial airplanes are sometimes pushed out of the passenger loading area by a tractor. (a) An 1800-kg tractor exerts a force of [latex]1 . \text{75} \times \text{10}^{4} \text{ N}[/latex] backward on the pavement, and the system experiences forces resisting motion that total 2400 N. If the acceleration is [latex]0 . \text{150 m}/\text{s}^{2}[/latex], what is the mass of the airplane? (b) Calculate the force exerted by the tractor on the airplane, assuming 2200 N of the friction is experienced by the airplane. (c) Draw two sketches showing the systems of interest used to solve each part, including the free-body diagrams for each.
  7. A 1100-kg car pulls a boat on a trailer. (a) What total force resists the motion of the car, boat, and trailer, if the car exerts a 1900-N force on the road and produces an acceleration of [latex]0 . \text{550 m}/\text{s}^{2}[/latex]? The mass of the boat plus trailer is 700 kg. (b) What is the force in the hitch between the car and the trailer if 80% of the resisting forces are experienced by the boat and trailer?
  8. (a) Find the magnitudes of the forces [latex]\textbf{F}_{1}[/latex] and [latex]\textbf{F}_{2}[/latex] that add to give the total force [latex]\textbf{F}_{\text{tot}}[/latex] shown in Figure 4.40. This may be done either graphically or by using trigonometry. (b) Show graphically that the same total force is obtained independent of the order of addition of [latex]\textbf{F}_{1}[/latex] and [latex]\textbf{F}_{2}[/latex]. (c) Find the direction and magnitude of some other pair of vectors that add to give [latex]\textbf{F}_{\text{tot}}[/latex]. Draw these to scale on the same drawing used in part (b) or a similar picture.
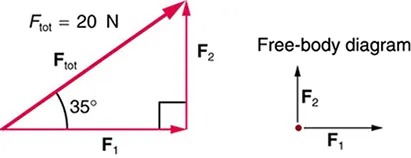
A right triangle is shown made up of three vectors. The first vector, F sub one, is along the triangle’s base toward the right; the second vector, F sub two, is along the perpendicular side pointing upward; and the third vector, F sub tot, is along the hypotenuse pointing up the incline. The magnitude of F sub tot is twenty newtons. In a free-body diagram, F sub one is shown by an arrow pointing right and F sub two is shown by an arrow acting vertically upward.

Figure 4.40 Image from OpenStax College Physics 2e, CC-BY 4.0

Image Description

The image consists of two diagrams related to forces:

1. Triangle Diagram on the Left:
– There is a right triangle with a hypotenuse labeled as \( F_{\text{tot}} \).
– \( F_{\text{tot}} = 20 \, \text{N} \) is written above the hypotenuse.
– The angle between the hypotenuse and the horizontal side is labeled \( 35^\circ \).
– The horizontal side of the triangle is labeled \( F_1 \).
– The vertical side of the triangle is labeled \( F_2 \).
– Both \( F_1 \) and \( F_2 \) have arrows indicating direction, with \( F_1 \) pointing right and \( F_2 \) pointing upward.

2. Free-body Diagram on the Right:
– This diagram consists of two arrows originating from the same point.
– One arrow is labeled \( F_1 \) and points horizontally to the right.
– The other arrow is labeled \( F_2 \) and points vertically upward.
– The label “Free-body diagram” is present near this setup.

Both diagrams are used to demonstrate the components of a resultant force using vector representation.

  1. Two children pull a third child on a snow saucer sled exerting forces [latex]\textbf{F}_{1}[/latex] and [latex]\textbf{F}_{2}[/latex] as shown from above in Figure 4.41. Find the acceleration of the 49.00-kg sled and child system. Note that the direction of the frictional force is unspecified; it will be in the opposite direction of the sum of [latex]\textbf{F}_{1}[/latex] and [latex]\textbf{F}_{2}[/latex].
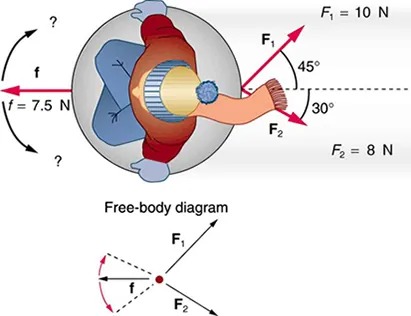
An overhead view of a child sitting on a snow saucer sled. Two forces, F sub one equal to ten newtons and F sub two equal to eight newtons, are acting toward the right. F sub one makes an angle of forty-five degrees from the x axis and F sub two makes an angle of thirty degrees from the x axis in a clockwise direction. A friction force f is equal to seven point five newtons, shown by a vector pointing in negative x direction. In the free-body diagram, F sub one and F sub two are shown by arrows toward the right, making a forty-five degree angle above the horizontal and a thirty-degree angle below the horizontal respectively. The friction force f is shown by an arrow along the negative x axis.

Figure 4.41 An overhead view of the horizontal forces acting on a child’s snow saucer sled. Image from OpenStax College Physics 2e, CC-BY 4.0

Image Description

The image shows a top-down view of a person sitting on a frictionless rotating stool, holding weights in each hand. The person is wearing a blue shirt and a yellow hat with a blue pom-pom. There are several forces and angles annotated around the person:

– Two forces, labeled as \(F_1\) and \(F_2\), are acting outward from the person’s hands. \(F_1\) is 10 N and is at a 45-degree angle to the right of the vertical axis. \(F_2\) is 8 N and is at a 30-degree angle to the left of the vertical axis.
– A frictional force \(f\) of 7.5 N acts against the direction of motion.
– The diagram shows suggested directions for movement with question marks.

Below this, there is a separate “Free-body diagram” showing the vectors of forces. Here, \(F_1\), \(F_2\), and \(f\) are represented with dashed lines, illustrating their directions.

The overall image appears to illustrate the concept of forces acting on a person rotating on a frictionless surface, highlighting the balances and interactions between different forces.

  1. Suppose your car was mired deeply in the mud and you wanted to use the method illustrated in Figure 4.42 to pull it out. (a) What force would you have to exert perpendicular to the center of the rope to produce a force of 12,000 N on the car if the angle is 2.00°? In this part, explicitly show how you follow the steps in the Problem-Solving Strategy for Newton’s laws of motion. (b) Real ropes stretch under such forces. What force would be exerted on the car if the angle increases to 7.00° and you still apply the force found in part (a) to its center?

Figure 4.42 Image from OpenStax College Physics 2e, CC-BY 4.0

Image Description

The image is a diagram showing a scenario where a vehicle is stuck and is being pulled using a winch connected to a tree trunk. The diagram includes:

– A blue car on the left side, positioned on a dirt surface.
– A tree trunk on the right side, depicted in green.
– A dotted line representing a cable extending from the tree trunk to the car.
– The cable is slightly sagging in the middle, forming an angle denoted as θ.
– Red arrows indicating tension (labeled as T) are directed outward from both the car and the tree trunk along the cable.
– In the middle of the cable, there’s a red vertical arrow pointing downwards, labeled as Fg, representing the force of gravity acting on the cable.

The background shows a gradient of colors suggesting an outdoor setting, possibly with grass and dirt.

  1. What force is exerted on the tooth in Figure 4.43 if the tension in the wire is 25.0 N? Note that the force applied to the tooth is smaller than the tension in the wire, but this is necessitated by practical considerations of how force can be applied in the mouth. Explicitly show how you follow steps in the Problem-Solving Strategy for Newton’s laws of motion.
Cross-section of jaw with sixteen teeth is shown. Braces are along the outside of the teeth. Three forces are acting on the protruding tooth. A force, T, is shown by an arrow making an angle of fifteen degrees below the positive x axis, and a second force, T, is shown by an arrow making an angle of fifteen degrees below the negative x axis.

Figure 4.43 Braces are used to apply forces to teeth to realign them. Shown in this figure are the tensions applied by the wire to the protruding tooth. The total force applied to the tooth by the wire, [latex]\textbf{F}_{\text{app}}[/latex], points straight toward the back of the mouth. Image from OpenStax College Physics 2e, CC-BY 4.0

Image Description

The image is an illustration of the upper jaw, viewed from above, showing the arrangement of teeth. The upper dental arch is depicted with the teeth arranged in a semi-circular formation. Above this, there are two arrows pointing outward from the center with a 15-degree angle labeled between them. These arrows are marked with the letter “T.” The teeth appear to be outlined, and there is some shading to suggest the gums. The focus of the image is likely on the 15-degree angle between the arrows as they relate to the alignment or force applied to the dental arch.

  1. Figure 4.44 shows Superhero and Trusty Sidekick hanging motionless from a rope. Superhero’s mass is 90.0 kg, while Trusty Sidekick’s is 55.0 kg, and the mass of the rope is negligible. (a) Draw a free-body diagram of the situation showing all forces acting on Superhero, Trusty Sidekick, and the rope. (b) Find the tension in the rope above Superhero. (c) Find the tension in the rope between Superhero and Trusty Sidekick. Indicate on your free-body diagram the system of interest used to solve each part.
Two caped superheroes hang on a rope suspended vertically from a bar.

Figure 4.44 Superhero and Trusty Sidekick hang motionless on a rope as they try to figure out what to do next. Will the tension be the same everywhere in the rope? Image from OpenStax College Physics 2e, CC-BY 4.0

Image Description

The image depicts a scene where two individuals dressed as superheroes are engaged in an action sequence. The superhero at the top is wearing a purple cape and boots with a gray costume. This character is holding onto a horizontal bar and hanging upside down. Below this character, another superhero is hanging on to the first individual’s ankles. The second superhero is dressed in a yellow and blue costume with teal boots and gloves. Both characters are positioned vertically, with the purple-caped superhero at the top and the yellow-and-blue-costumed superhero beneath, as if participating in a rescue or climbing scenario.

  1. A nurse pushes a cart by exerting a force on the handle at a downward angle [latex]\text{35}.\text{0}º[/latex] below the horizontal. The loaded cart has a mass of 28.0 kg, and the force of friction is 60.0 N. (a) Draw a free-body diagram for the system of interest. (b) What force must the nurse exert to move at a constant velocity?
  2. Construct Your Own Problem Consider the tension in an elevator cable during the time the elevator starts from rest and accelerates its load upward to some cruising velocity. Taking the elevator and its load to be the system of interest, draw a free-body diagram. Then calculate the tension in the cable. Among the things to consider are the mass of the elevator and its load, the final velocity, and the time taken to reach that velocity.
  3. Construct Your Own Problem Consider two people pushing a toboggan with four children on it up a snow-covered slope. Construct a problem in which you calculate the acceleration of the toboggan and its load. Include a free-body diagram of the appropriate system of interest as the basis for your analysis. Show vector forces and their components and explain the choice of coordinates. Among the things to be considered are the forces exerted by those pushing, the angle of the slope, and the masses of the toboggan and children.
  4. Unreasonable Results (a) Repeat Exercise 4.29, but assume an acceleration of [latex]1 . \text{20 m}/\text{s}^{2}[/latex] is produced. (b) What is unreasonable about the result? (c) Which premise is unreasonable, and why is it unreasonable?
  5. Unreasonable Results (a) What is the initial acceleration of a rocket that has a mass of [latex]1 . \text{50} \times \text{10}^{6} \text{ kg}[/latex] at takeoff, the engines of which produce a thrust of [latex]2 . \text{00} \times \text{10}^{6} \text{ N}[/latex]? Do not neglect gravity. (b) What is unreasonable about the result? (This result has been unintentionally achieved by several real rockets.) (c) Which premise is unreasonable, or which premises are inconsistent? (You may find it useful to compare this problem to the rocket problem earlier in this section.)

4.7 Further Applications of Newton’s Laws of Motion

  1. A flea jumps by exerting a force of [latex]1 . \text{20} \times \text{10}^{- 5} \text{ N}[/latex] straight down on the ground. A breeze blowing on the flea parallel to the ground exerts a force of [latex]0 . \text{500} \times \text{10}^{- 6} \text{ N}[/latex] on the flea. Find the direction and magnitude of the acceleration of the flea if its mass is [latex]6 . \text{00} \times \text{10}^{- 7} \text{ kg}[/latex]. Do not neglect the gravitational force.
  2. Two muscles in the back of the leg pull upward on the Achilles tendon, as shown in Figure 4.45. (These muscles are called the medial and lateral heads of the gastrocnemius muscle.) Find the magnitude and direction of the total force on the Achilles tendon. What type of movement could be caused by this force?
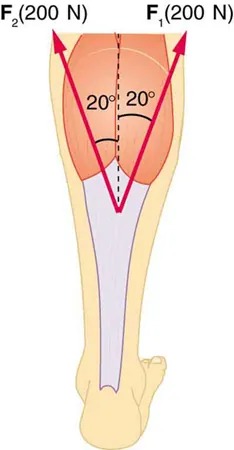
An Achilles tendon is shown in the figure with two forces acting upward, one at an angle of plus twenty degrees, one at minus twenty degrees. F sub one, equal to two hundred newtons, is shown by a vector making an angle twenty degrees toward the right with the vertical, and F sub two, equal to two hundred newtons, is shown making an angle of twenty degrees left from the vertical.

Figure 4.45 Achilles tendon Image from OpenStax College Physics 2e, CC-BY 4.0

Image Description

The image is an anatomical diagram of a leg viewed from the back, focusing on the muscles around the thigh and lower leg. It highlights the division of muscular forces in the leg.

– The thigh is depicted with two large muscles, and the diagram focuses on the forces exerted by these muscles.
– Two arrows, labeled as \( F_1 \) and \( F_2 \), represent forces of 200 Newtons each.
– These arrows point diagonally outward, away from each other and form a symmetrical “V” shape.
– Each arrow originates from the center of the thigh and indicates the direction of force exerted by the muscles.
– The angle between each force line (arrow) and the midline of the thigh is marked as 20 degrees.
– The forces diverge from a central point at the top of the thigh.

Overall, the image is a schematic representation illustrating how forces are distributed in the muscles of the leg, specifically around the thigh area.

  1. A 76.0-kg person is being pulled away from a burning building as shown in Figure 4.46. Calculate the tension in the two ropes if the person is momentarily motionless. Include a free-body diagram in your solution.
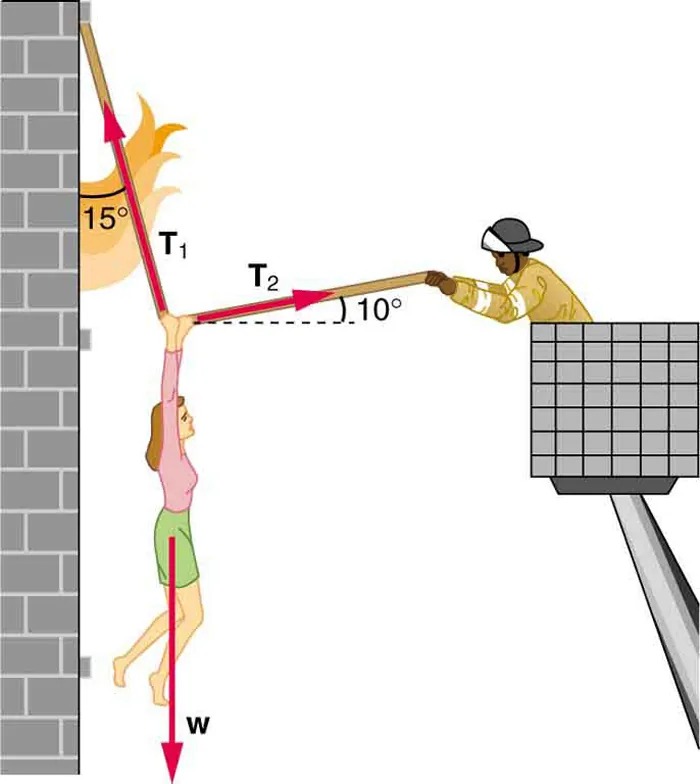
A lady is being pulled away from a burning building using a rope. She is in the middle of the rope; her weight is shown by a vector acting vertically downward. Tension, T sub one, acts upward through the left side of the rope, making an angle of fifteen degrees with the vertical. Tension T sub two acts through the right side of the rope, making an angle of ten degrees above the positive x axis.

Figure 4.46 The force [latex]\textbf{T}_{2}[/latex] needed to hold steady the person being rescued from the fire is less than her weight and less than the force [latex]\textbf{T}_{1}[/latex] in the other rope, since the more vertical rope supports a greater part of her weight Image from OpenStax College Physics 2e, CC-BY 4.0

Image Description

The image depicts a rescue scene involving a firefighter and a person being rescued from a burning building.

– On the left, there is a brick wall with flames visible, suggesting a fire. A person is hanging from the wall, holding onto a horizontal bar.
– The person, a woman, is suspended in mid-air and appears to be held by two forces represented by arrows labeled T1 and T2.
– T1 is angled at 15 degrees from the vertical, pointing upwards toward the wall.
– T2 is angled at 10 degrees from the horizontal, pointing towards the right where the firefighter is located.
– The woman’s body is aligned with the direction of arrow T1, indicating tension or force in that direction.
– A downward arrow labeled “w” points straight down from the woman, indicating her weight or the force of gravity acting on her.
– To the right, a firefighter is standing in a basket attached to a ladder, reaching out with a stick or pole to assist the person.
– The firefighter is wearing protective gear, including a helmet.
– The basket is part of an extendable platform, positioning the firefighter at the same height as the hanging woman.

This illustration appears to be a physics-based diagram illustrating tension, force, and angle relationships in the context of a practical rescue scenario.

  1. Integrated Concepts A 35.0-kg dolphin decelerates from 12.0 to 7.50 m/s in 2.30 s to join another dolphin in play. What average force was exerted to slow him if he was moving horizontally? (The gravitational force is balanced by the buoyant force of the water.)
  2. Integrated Concepts When starting a foot race, a 70.0-kg sprinter exerts an average force of 650 N backward on the ground for 0.800 s. (a) What is his final speed? (b) How far does he travel?
  3. Integrated Concepts A large rocket has a mass of [latex]2 . \text{00} \times \text{10}^{6} \text{ kg}[/latex] at takeoff, and its engines produce a thrust of [latex]3 . \text{50} \times \text{10}^{7} \text{ N}[/latex]. (a) Find its initial acceleration if it takes off vertically. (b) How long does it take to reach a velocity of 120 km/h straight up, assuming constant mass and thrust? (c) In reality, the mass of a rocket decreases significantly as its fuel is consumed. Describe qualitatively how this affects the acceleration and time for this motion.
  4. Integrated Concepts A basketball player jumps straight up for a ball. To do this, they lower their body 0.300 m and then accelerate through this distance by forcefully straightening their legs. This player leaves the floor with a vertical velocity sufficient to carry the player 0.900 m above the floor. (a) Calculate the player’s velocity when they leave the floor. (b) Calculate their acceleration while they are straightening their legs. They go from zero to the velocity found in part (a) in a distance of 0.300 m. (c) Calculate the force they exert on the floor to do this, given that their mass is 110 kg.
  5. Integrated Concepts A 2.50-kg fireworks shell is fired straight up from a mortar and reaches a height of 110 m. (a) Neglecting air resistance (a poor assumption, but we will make it for this example), calculate the shell’s velocity when it leaves the mortar. (b) The mortar itself is a tube 0.450 m long. Calculate the average acceleration of the shell in the tube as it goes from zero to the velocity found in (a). (c) What is the average force on the shell in the mortar? Express your answer in newtons and as a ratio to the weight of the shell.
  6. Integrated Concepts Repeat Exercise 4.47 for a shell fired at an angle [latex]\text{10}.\text{0}º[/latex] from the vertical.
  7. Integrated Concepts An elevator filled with passengers has a mass of 1700 kg. (a) The elevator accelerates upward from rest at a rate of [latex]1 . \text{20 m}/\text{s}^{2}[/latex] for 1.50 s. Calculate the tension in the cable supporting the elevator. (b) The elevator continues upward at constant velocity for 8.50 s. What is the tension in the cable during this time? (c) The elevator decelerates at a rate of [latex]0 . \text{600 m}/\text{s}^{2}[/latex] for 3.00 s. What is the tension in the cable during deceleration? (d) How high has the elevator moved above its original starting point, and what is its final velocity?
  8. Unreasonable Results (a) What is the final velocity of a car originally traveling at 50.0 km/h that decelerates at a rate of [latex]0 . \text{400 m}/\text{s}^{2}[/latex] for 50.0 s? (b) What is unreasonable about the result? (c) Which premise is unreasonable, or which premises are inconsistent?
  9. Unreasonable Results A 75.0-kg man stands on a bathroom scale in an elevator that accelerates from rest to 30.0 m/s in 2.00 s. (a) Calculate the scale reading in newtons and compare it with his weight. (The scale exerts an upward force on him equal to its reading.) (b) What is unreasonable about the result? (c) Which premise is unreasonable, or which premises are inconsistent?

4.8 Extended Topic: The Four Basic Forces—An Introduction

  1. (a) What is the strength of the weak nuclear force relative to the strong nuclear force? (b) What is the strength of the weak nuclear force relative to the electromagnetic force? Since the weak nuclear force acts at only very short distances, such as inside nuclei, where the strong and electromagnetic forces also act, it might seem surprising that we have any knowledge of it at all. We have such knowledge because the weak nuclear force is responsible for beta decay, a type of nuclear decay not explained by other forces.
  2. (a) What is the ratio of the strength of the gravitational force to that of the strong nuclear force? (b) What is the ratio of the strength of the gravitational force to that of the weak nuclear force? (c) What is the ratio of the strength of the gravitational force to that of the electromagnetic force? What do your answers imply about the influence of the gravitational force on atomic nuclei?
  3. What is the ratio of the strength of the strong nuclear force to that of the electromagnetic force? Based on this ratio, you might expect that the strong force dominates the nucleus, which is true for small nuclei. Large nuclei, however, have sizes greater than the range of the strong nuclear force. At these sizes, the electromagnetic force begins to affect nuclear stability. These facts will be used to explain nuclear fusion and fission later in this text.
  4. Critical Thinking Two boxes of equal mass slide start from rest and slide with different horizontal applied forces across frictionless surfaces to reach the same distance away. Box A has a horizontal force of three times that of box B. (a) Which box is traveling faster at this distance away from the starting point? Briefly explain your reasoning. (b) Based on experimental data, an equation that fits the data is suggested for the final speed, V, which may not be correct: [latex]V = K F[/latex], where K is a constant with appropriate units and F is the horizontal applied force. Is this equation consistent with your answer from part a? Explain why or why not. Does this equation make sense? Explain why or why not. (c) Now the applied force can be any value and the distance from the starting point is measured when the speed gets to a consistent value. Graph the distance the box gets to at a given speed as a function of the applied force.

4.9 Friction

  1. A physics major is cooking breakfast when he notices that the frictional force between his steel spatula and his Teflon frying pan is only 0.200 N. Knowing the coefficient of kinetic friction between the two materials, he quickly calculates the normal force. What is it?
  2. (a) When rebuilding her car’s engine, a physics major must exert 300 N of force to insert a dry steel piston into a steel cylinder. What is the magnitude of the normal force between the piston and cylinder? (b) What is the magnitude of the force would she have to exert if the steel parts were oiled?
  3. (a) What is the maximum frictional force in the knee joint of a person who supports 66.0 kg of her mass on that knee? (b) During strenuous exercise it is possible to exert forces to the joints that are easily ten times greater than the weight being supported. What is the maximum force of friction under such conditions? The frictional forces in joints are relatively small in all circumstances except when the joints deteriorate, such as from injury or arthritis. Increased frictional forces can cause further damage and pain.
  4. Suppose you have a 120-kg wooden crate resting on a wood floor. (a) What maximum force can you exert horizontally on the crate without moving it? (b) If you continue to exert this force once the crate starts to slip, what will the magnitude of its acceleration then be?
  5. (a) If half of the weight of a small [latex]1 . \text{00} \times \text{10}^{3} \text{kg}[/latex]utility truck is supported by its two drive wheels, what is the magnitude of the maximum acceleration it can achieve on dry concrete? (b) Will a metal cabinet lying on the wooden bed of the truck slip if it accelerates at this rate? (c) Solve both problems assuming the truck has four-wheel drive.
  6. A team of eight dogs pulls a sled with waxed wood runners on wet snow (mush!). The dogs have average masses of 19.0 kg, and the loaded sled with its rider has a mass of 210 kg. (a) Calculate the magnitude of the acceleration starting from rest if each dog exerts an average force of 185 N backward on the snow. (b) What is the magnitude of the acceleration once the sled starts to move? (c) For both situations, calculate the magnitude of the force in the coupling between the dogs and the sled.
  7. Consider the 65.0-kg ice skater being pushed by two others shown in Figure 4.47. (a) Find the direction and magnitude of [latex]\mathbf{F}_{\text{tot}}[/latex], the total force exerted on her by the others, given that the magnitudes [latex]F_{1}[/latex] and [latex]F_{2}[/latex] are 26.4 N and 18.6 N, respectively. (b) What is her initial acceleration if she is initially stationary and wearing steel-bladed skates that point in the direction of [latex]\mathbf{F}_{\text{tot}}[/latex]? (c) What is her acceleration assuming she is already moving in the direction of [latex]\mathbf{F}_{\text{tot}}[/latex]? (Remember that friction always acts in the direction opposite that of motion or attempted motion between surfaces in contact.)
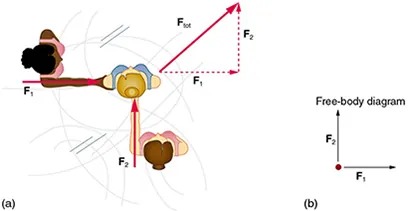
(a) Overhead view of two ice skaters pushing on a third. One skater pushes with a force F two, represented by an arrow pointing up, and a second skater pushes with a force F one, represented by an arrow pointing from left to right. Vector F one and vector F two are along the arms of the two skaters acting on the third skater. A vector diagram is shown in the form of a right triangle in which the base is vector F one pointing east, and perpendicular to F one is vector F two pointing north. The resultant vector is shown by the hypotenuse pointing northeast. (b) Free-body diagram showing only the forces acting on the skater.

Figure 4.47 Image from OpenStax College Physics 2e, CC-BY 4.0

Image Description

The image consists of two parts labeled (a) and (b).

Part (a):
– Shows a top-down view of three individuals engaged in a tug-of-war on a frictionless platform.
– The individuals are positioned in a triangular formation.
– There are two forces labeled \( F_1 \) and \( F_2 \) with arrows showing direction and magnitude.
– \( F_1 \) is directed towards the right, and \( F_2 \) is directed upwards.
– A resultant force \( F_{\text{tot}} \) is indicated by a dashed arrow pointing diagonally upwards and to the right.

Part (b):
– Depicts a simplified free-body diagram.
– Shows a red point with two perpendicular arrows.
– The horizontal arrow is labeled \( F_1 \) (pointing right), and the vertical arrow is labeled \( F_2 \) (pointing up).
– The label “Free-body diagram” is positioned above these arrows.

The image illustrates the concept of combining forces and creating a vector diagram to represent the interaction visually.

  1. Show that the acceleration of any object down a frictionless incline that makes an angle [latex]\theta[/latex] with the horizontal is [latex]a = g \text{sin} \theta[/latex]. (Note that this acceleration is independent of mass.)
  2. Show that the acceleration of any object down an incline where friction behaves simply (that is, where [latex]f_{\text{k}} = \mu_{\text{k}} N[/latex]) is [latex]a = g \left(\right. \text{sin} \theta - \mu_{\text{k}} \text{cos} \theta ).[/latex] Note that the acceleration is independent of mass and reduces to the expression found in the previous problem when friction becomes negligibly small [latex]\left(\right. \mu_{\text{k}} = 0 ).[/latex]
  3. Calculate the deceleration of a snow boarder going up a [latex]5.0º[/latex], slope assuming the coefficient of friction for waxed wood on wet snow. The result of Exercise 4.64 may be useful, but be careful to consider the fact that the snow boarder is going uphill. Explicitly show how you follow the steps in 4.6 Problem-Solving Strategies.
  4. (a) Calculate the acceleration of a skier heading down a [latex]\text{10} . 0º[/latex] slope, assuming the coefficient of friction for waxed wood on wet snow. (b) Find the angle of the slope down which this skier could coast at a constant velocity. You can neglect air resistance in both parts, and you will find the result of Exercise 4.64 to be useful. Explicitly show how you follow the steps in 4.6 Problem-Solving Strategies.
  5. If an object is to rest on an incline without slipping, then friction must equal the component of the weight of the object parallel to the incline. This requires greater and greater friction for steeper slopes. Show that the maximum angle of an incline above the horizontal for which an object will not slide down is [latex]\theta = \text{tan}^{–\text{1}} \mu_{\text{s}}[/latex]. You may use the result of the previous problem. Assume that [latex]a = \text{0}[/latex] and that static friction has reached its maximum value.
  6. Calculate the maximum deceleration of a car that is heading down a [latex]6º[/latex] slope (one that makes an angle of [latex]6º[/latex] with the horizontal) under the following road conditions. You may assume that the weight of the car is evenly distributed on all four tires and that the coefficient of static friction is involved—that is, the tires are not allowed to slip during the deceleration. (Ignore rolling.) Calculate for a car: (a) On dry concrete. (b) On wet concrete. (c) On ice, assuming that [latex]\mu_{s} = 0 . \text{100}[/latex], the same as for shoes on ice.
  7. Calculate the maximum acceleration of a car that is heading up a
    [latex]\text{4}º[/latex] slope (one that makes an angle of
    [latex]\text{4}º[/latex] with the horizontal) under the following road conditions. Assume that only half the weight of the car is supported by the two drive wheels and that the coefficient of static friction is involved—that is, the tires are not allowed to slip during the acceleration. (Ignore rolling.) (a) On dry concrete. (b) On wet concrete. (c) On ice, assuming that [latex]\mu_{\text{s}} = \text{0}.\text{100}[/latex], the same as for shoes on ice.
  8. Repeat Exercise 4.69 for a car with four-wheel drive.
  9. A freight train consists of two [latex]8 . \text{00} \times \text{10}^{5} -\text{kg}[/latex] engines and 45 cars with average masses of [latex]5 . \text{50} \times \text{10}^{5} \text{ kg}[/latex]. (a) What force must each engine exert backward on the track to accelerate the train at a rate of [latex]5 . \text{00} \times \text{10}^{- 2} m / s^{2}[/latex] if the force of friction is [latex]7 . \text{50} \times \text{10}^{5} N[/latex], assuming the engines exert identical forces? This is not a large frictional force for such a massive system. Rolling friction for trains is small, and consequently trains are very energy-efficient transportation systems. (b) What is the magnitude of the force in the coupling between the 37th and 38th cars (this is the force each exerts on the other), assuming all cars have the same mass and that friction is evenly distributed among all of the cars and engines?
  10. Consider the 52.0-kg mountain climber in Figure 4.48. (a) Find the tension in the rope and the force that the mountain climber must exert with her feet on the vertical rock face to remain stationary. Assume that the force is exerted parallel to her legs. Also, assume negligible force exerted by her arms. (b) What is the minimum coefficient of friction between her shoes and the cliff?
A mountain climber with a mass of fifty two kilograms exerts force with her feet parallel to her legs on a vertical rock face to remain stationary. The angle between her legs and the rock face is fifteen degrees, whereas the angle between the rope and the cliff is thirty one degrees.

Figure 4.48 Part of the climber’s weight is supported by her rope and part by friction between her feet and the rock face. Image from OpenStax College Physics 2e, CC-BY 4.0

Image Description

The image illustrates a person rock climbing with two key angles and force vectors depicted. The climber, wearing athletic clothing, is pulling on a rope with both hands. The rope is oriented at a 31-degree angle relative to the rock wall. Two arrows indicating force are shown: one labeled “T” points along the rope towards the climber, representing tension in the rope, and the other labeled “Flegs” extends from the climber’s feet, pushing against the wall to maintain position. The force from the climber’s legs forms a 15-degree angle relative to the horizontal line below their feet. The rock wall has a textured appearance with cracks and ledges, suggesting a natural climbing environment.

  1. A contestant in a winter sporting event pushes a 45.0-kg block of ice across a frozen lake as shown in Figure 5.21(a). (a) Calculate the minimum force [latex]F[/latex] he must exert to get the block moving. (b) What is the magnitude of its acceleration once it starts to move, if that force is maintained?
  2. Repeat Exercise 4.73 with the contestant pulling the block of ice with a rope over his shoulder at the same angle above the horizontal as shown in Figure 4.49(b).
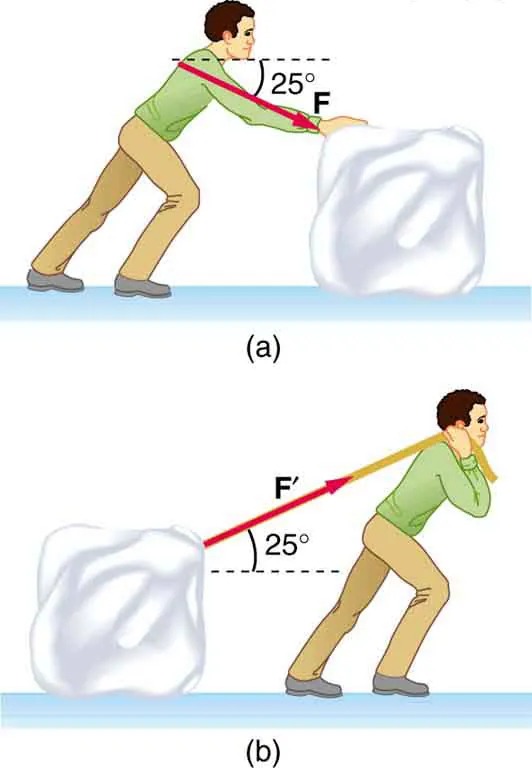
(a) A block of ice is being pushed by a contestant in a winter sporting event across a frozen lake at an angle of twenty five degrees. (b) A block of ice is being pulled by a contestant in a winter sporting event across a frozen lake at an angle of twenty five degrees.

Figure 4.49 Which method of sliding a block of ice requires less force—(a) pushing or (b) pulling at the same angle above the horizontal? Image from OpenStax College Physics 2e, CC-BY 4.0

Image Description

The image consists of two diagrams, labeled (a) and (b), illustrating a person moving a large object that resembles a block of ice.

– Diagram (a): A person is pushing the block. The diagram shows the person leaning forward, with their hands placed on the back of the block. An arrow labeled “F” is drawn from the person’s shoulders to the block, making an angle of 25 degrees downward from the horizontal. This suggests that the force is applied with an angle towards the floor.

– Diagram (b): A person is pulling the block using a rope or similar object. The diagram shows the person leaning backward with the pulling object wrapped around their shoulder. An arrow labeled “F'” extends from the block to the person’s shoulders, making an angle of 25 degrees upward from the horizontal. This indicates that the pulling force is directed slightly upwards.

Both diagrams demonstrate the angles and direction of force application in pushing and pulling scenarios.

“Chapter 4: Problems & Exercises” from College Physics 2e by OpenStax is licensed under a Creative Commons Attribution 4.0 International License.
“Chapter 5: Problems & Exercises” from College Physics 2e by OpenStax is licensed under a Creative Commons Attribution 4.0 International License.

License

Icon for the Creative Commons Attribution 4.0 International License

College Physics Copyright © 2025 by Dr. Iftekhar Haque is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book