2.1 Displacement
Learning Objectives
By the end of this section, you will be able to:
- Define position, displacement, distance, and distance traveled.
- Explain the relationship between position and displacement.
- Distinguish between displacement and distance traveled.
- Calculate displacement and distance given initial position, final position, and the path between the two.

Figure 2.2 These cyclists in Vietnam can be described by their position relative to buildings and a canal. Their motion can be described by their change in position, or displacement, in the frame of reference. Image from OpenStax College Physics 2e, CC-BY 4.0
Position
In order to describe the motion of an object, you must first be able to describe its position—where it is at any particular time. More precisely, you need to specify its position relative to a convenient reference frame. Earth is often used as a reference frame, and we often describe the position of an object as it relates to stationary objects in that reference frame. For example, a rocket launch would be described in terms of the position of the rocket with respect to the Earth as a whole, while a professor’s position could be described in terms of where she is in relation to the nearby white board. (See Figure 2.3.) In other cases, we use reference frames that are not stationary but are in motion relative to the Earth. To describe the position of a person in an airplane, for example, we use the airplane, not the Earth, as the reference frame. (See Figure 2.4.)
Displacement
If an object moves relative to a reference frame (for example, if a professor moves to the right relative to a white board or a passenger moves toward the rear of an airplane), then the object’s position changes. This change in position is known as displacement. The word “displacement” implies that an object has moved, or has been displaced.
Displacement
Displacement is the change in position of an object:
[latex]\Delta x = x_{\text{f}} - x_{0} ,[/latex]
where [latex]\Delta x[/latex] is displacement, [latex]x_{\text{f}}[/latex] is the final position, and [latex]x_{0}[/latex] is the initial position.
In this text the upper case Greek letter [latex]\Delta[/latex] (delta) always means “change in” whatever quantity follows it; thus, [latex]\Delta x[/latex] means change in position. Always solve for displacement by subtracting initial position [latex]x_{0}[/latex] from final position [latex]x_{\text{f}}[/latex].
Note that the SI unit for displacement is the meter (m) (see 1.2 Physical Quantities and Units), but sometimes kilometers, miles, feet, and other units of length are used. Keep in mind that when units other than the meter are used in a problem, you may need to convert them into meters to complete the calculation.
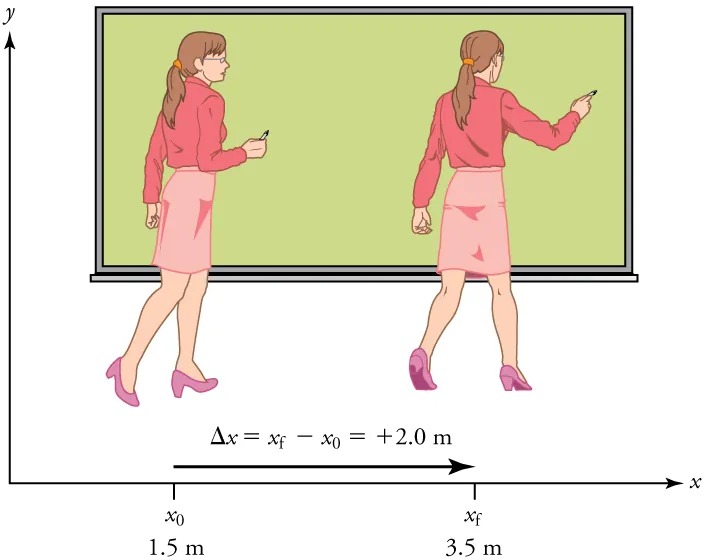
Figure 2.3 A professor paces left and right while lecturing. Her position relative to Earth is given by [latex]x[/latex]. The [latex]+ 2 . 0 \text{m}[/latex] displacement of the professor relative to Earth is represented by an arrow pointing to the right. Image from OpenStax College Physics 2e, CC-BY 4.0
Image Description
The image shows two illustrations of a woman in front of a chalkboard, indicating a depiction of motion along the x-axis.
– Left Side: The woman is facing to the right, standing in front of a chalkboard. She is holding a pen or marker in her right hand and is wearing a pink skirt and a red blouse. Her initial position, labeled as \( x_0 \), is marked at 1.5 meters along the x-axis.
– Right Side: The woman is in the same outfit but now turned slightly towards the board, indicating her final position. She is holding the pen or marker up to the board. Her final position, labeled as \( x_f \), is marked at 3.5 meters along the x-axis.
– Background: A large green chalkboard is behind her, framed in black.
– Mathematics: Below the woman are mathematical equations depicting the change in position \( \Delta x \), which is calculated as \( x_f – x_0 = +2.0 \, \text{m} \). An arrow points to the right, indicating the direction of motion.
– Axes: The x-axis is labeled at the bottom, with arrows on both ends pointing horizontally. The y-axis points vertically upwards on the left side.
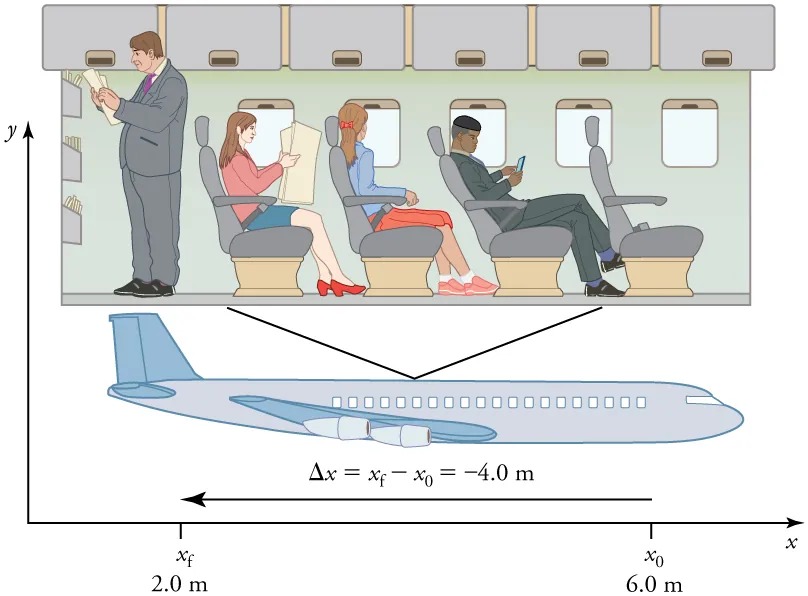
Figure 2.4 A passenger moves from his seat to the back of the plane. His location relative to the airplane is given by [latex]x[/latex]. The [latex]- 4 . 0 -\text{m}[/latex] displacement of the passenger relative to the plane is represented by an arrow toward the rear of the plane. Notice that the arrow representing his displacement is twice as long as the arrow representing the displacement of the professor (he moves twice as far) in . Image from OpenStax College Physics 2e, CC-BY 4.0
Image Description
The image shows a cross-section of an airplane cabin viewed from the side. Inside the cabin, there are four passengers and one flight attendant.
- The flight attendant is standing at the front of the cabin, facing forward. There are storage compartments above.
- Four passengers are seated in a row:
- The first passenger is reading a newspaper.
- The second is using a phone.
- The third passenger is a woman with red hair, also using a phone.
- The fourth passenger, a man wearing a hat, is looking at a tablet.
Below the cabin is an illustration of a complete airplane showing its exterior profile. Two lines extend from the outside of the cabin to the ends of the airplane, depicting the horizontal distance.
| Δx = xf – x0 = -4.0 m |
| xf = 2.0 m |
| x0 = 6.0 m |
Axes are shown with y pointing upwards and x pointing towards the right, indicating horizontal and vertical orientation.
Note that displacement has a direction as well as a magnitude. The professor’s displacement is 2.0 m to the right, and the airline passenger’s displacement is 4.0 m toward the rear. In one-dimensional motion, direction can be specified with a plus or minus sign. When you begin a problem, you should select which direction is positive (usually that will be to the right or up, but you are free to select positive as being any direction). The professor’s initial position is [latex]x_{0} = 1 . 5 \text{m}[/latex] and her final position is [latex]x_{\text{f}} = 3 . 5 \text{m}[/latex]. Thus her displacement is
[latex]Δ x = x_{f} - x_{0} = 3 .\text{5 m} - 1.5 m = + 2 .\text{0 m} .[/latex]
In this coordinate system, motion to the right is positive, whereas motion to the left is negative. Similarly, the airplane passenger’s initial position is [latex]x_{0} = 6 . 0 m[/latex] and his final position is [latex]x_{f} = 2 . 0 m[/latex], so his displacement is
[latex]Δ x = x_{f} - x_{0} = 2 . 0 m - 6 . 0 m = - 4 . 0 m .[/latex]
His displacement is negative because his motion is toward the rear of the plane, or in the negative [latex]x[/latex] direction in our coordinate system.
Distance
Although displacement is described in terms of direction, distance is not. Distance is defined to be the magnitude or size of displacement between two positions. Note that the distance between two positions is not the same as the distance traveled between them. Distance traveled is the total length of the path traveled between two positions. Distance has no direction and, thus, no sign. For example, the distance the professor walks is 2.0 m. The distance the airplane passenger walks is 4.0 m.
Misconception Alert: Distance Traveled vs. Magnitude of Displacement
It is important to note that the distance traveled, however, can be greater than the magnitude of the displacement (by magnitude, we mean just the size of the displacement without regard to its direction; that is, just a number with a unit). For example, the professor could pace back and forth many times, perhaps walking a distance of 150 m during a lecture, yet still end up only 2.0 m to the right of her starting point. In this case her displacement would be +2.0 m, the magnitude of her displacement would be 2.0 m, but the distance she traveled would be 150 m. In kinematics we nearly always deal with displacement and magnitude of displacement, and almost never with distance traveled. One way to think about this is to assume you marked the start of the motion and the end of the motion. The displacement is simply the difference in the position of the two marks and is independent of the path taken in traveling between the two marks. The distance traveled, however, is the total length of the path taken between the two marks.
Check Your Understanding
A cyclist rides 3 km west and then turns around and rides 2 km east. (a) What is their displacement? (b) What distance do they ride? (c) What is the magnitude of their displacement?
Click for Solution
Solution
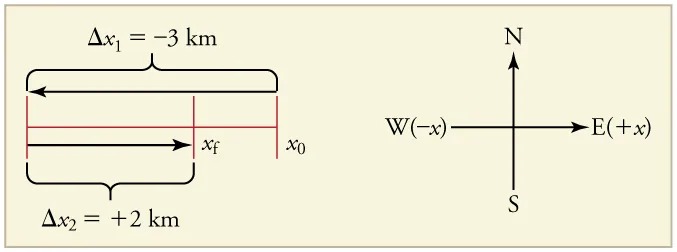
Figure 2.5 Image from OpenStax College Physics 2e, CC-BY 4.0
Image Description
The image consists of two main parts:
1. Left Side:
– There is a horizontal line segment labeled with the endpoints \( x_0 \) and \( x_f \).
– Two distances are indicated along this line:
– The section from \( x_0 \) to a point on the left is labeled as \( \Delta x_1 = -3 \, \text{km} \) with an arrow pointing left. A curly bracket shows this distance.
– The section from a point on the left to \( x_f \) is labeled as \( \Delta x_2 = +2 \, \text{km} \) with an arrow pointing right. Another curly bracket shows this distance.
2. Right Side:
– A compass rose indicates directions with arrows pointing:
– Upward for North (N)
– Right for East (E) labeled as \( (+x) \)
– Downward for South (S)
– Left for West (W) labeled as \( (-x) \)
(a) The rider’s displacement is
[latex]Δ x = x_{\text{f}} - x_{0} = −\text{1 km}[/latex].
(The displacement is negative because we take east to be positive and west to be negative.)
(b) The distance traveled is [latex]\text{3 km } + \text{ 2 km } = \text{ 5 km}[/latex].
(c) The magnitude of the displacement is [latex]1 km[/latex].

