17.11 More Applications of Magnetism

Mass Spectrometry

The curved paths followed by charged particles in magnetic fields can be put to use. A charged particle moving perpendicular to a magnetic field travels in a circular path having a radius [latex]r[/latex].

It was noted that this relationship could be used to measure the mass of charged particles such as ions. A mass spectrometer is a device that measures such masses. Most mass spectrometers use magnetic fields for this purpose, although some of them have extremely sophisticated designs. Since there are five variables in the relationship, there are many possibilities. However, if [latex]v[/latex], [latex]q[/latex], and [latex]B[/latex] can be fixed, then the radius of the path [latex]r[/latex] is simply proportional to the mass [latex]m[/latex] of the charged particle. Let us examine one such mass spectrometer that has a relatively simple design. (See Figure 17.41.) The process begins with an ion source, a device like an electron gun. The ion source gives ions their charge, accelerates them to some velocity [latex]v[/latex], and directs a beam of them into the next stage of the spectrometer. This next region is a velocity selector that only allows particles with a particular value of [latex]v[/latex] to get through.

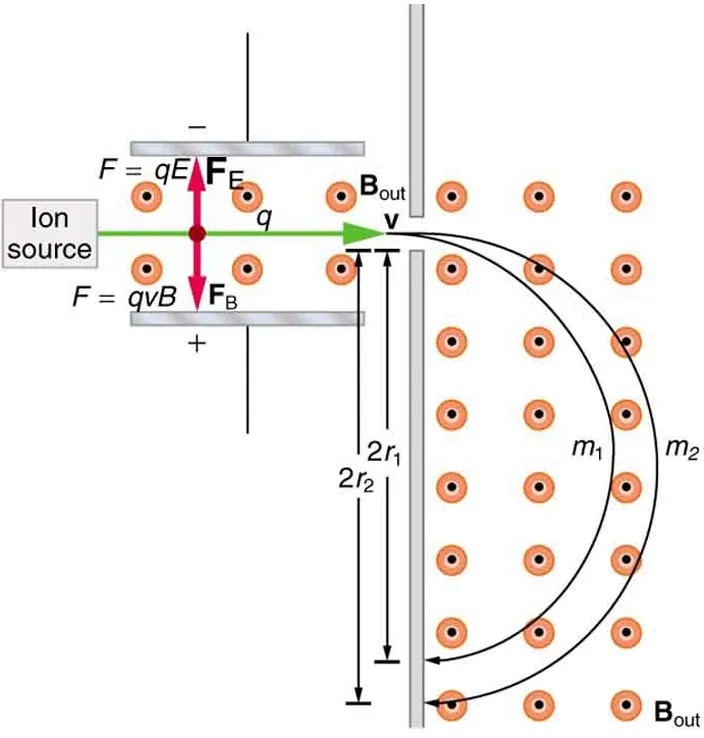
Figure 17.41 This mass spectrometer uses a velocity selector to fix [latex]v[/latex] so that the radius of the path is proportional to mass. Image from OpenStax College Physics 2e, CC-BY 4.0

The velocity selector has both an electric field and a magnetic field, perpendicular to one another, producing forces in opposite directions on the ions. Only those ions for which the forces balance travel in a straight line into the next region. If the forces balance, then the electric force [latex]F = \text{qE}[/latex] equals the magnetic force [latex]F = \text{qvB}[/latex], so that [latex]\text{qE} = \text{qvB}[/latex]. Noting that [latex]q[/latex] cancels, we see that

is the velocity particles must have to make it through the velocity selector, and further, that [latex]v[/latex] can be selected by varying [latex]E[/latex] and [latex]B[/latex]. In the final region, there is only a uniform magnetic field, and so the charged particles move in circular arcs with radii proportional to particle mass. The paths also depend on charge [latex]q[/latex], but since [latex]q[/latex] is in multiples of electron charges, it is easy to determine and to discriminate between ions in different charge states.

Mass spectrometry today is used extensively in chemistry and biology laboratories to identify chemical and biological substances according to their mass-to-charge ratios. In medicine, mass spectrometers are used to measure the concentration of isotopes used as tracers. Usually, biological molecules such as proteins are very large, so they are broken down into smaller fragments before analyzing. Recently, large virus particles have been analyzed as a whole on mass spectrometers. Sometimes a gas chromatograph or high-performance liquid chromatograph provides an initial separation of the large molecules, which are then input into the mass spectrometer.

Cathode Ray Tubes—CRTs—and the Like

What do non-flat-screen TVs, old computer monitors, x-ray machines, and the 2-mile-long Stanford Linear Accelerator have in common? All of them accelerate electrons, making them different versions of the electron gun. Many of these devices use magnetic fields to steer the accelerated electrons. Figure 17.42 shows the construction of the type of cathode ray tube (CRT) found in some TVs, oscilloscopes, and old computer monitors. Two pairs of coils are used to steer the electrons, one vertically and the other horizontally, to their desired destination.

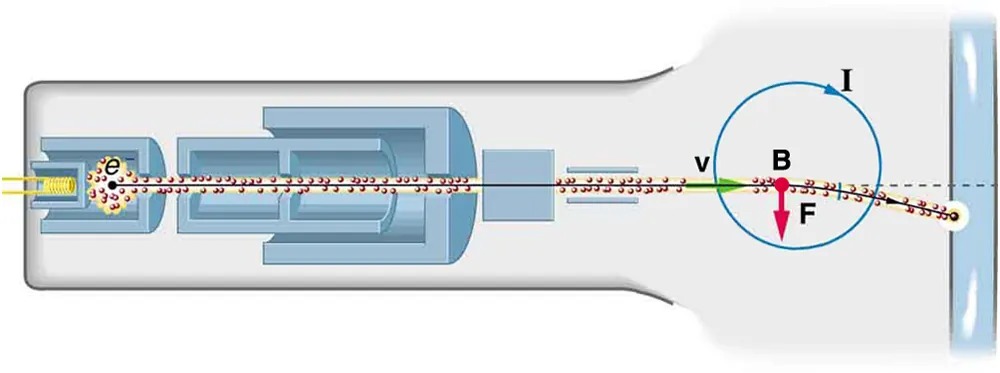
Figure 17.42 The cathode ray tube (CRT) is so named because rays of electrons originate at the cathode in the electron gun. Magnetic coils are used to steer the beam in many CRTs. In this case, the beam is moved down. Another pair of horizontal coils would steer the beam horizontally. Image from OpenStax College Physics 2e, CC-BY 4.0

Magnetic Resonance Imaging

Magnetic resonance imaging (MRI) is one of the most useful and rapidly growing medical imaging tools. It non-invasively produces two-dimensional and three-dimensional images of the body that provide important medical information with none of the hazards of x-rays. MRI is based on an effect called nuclear magnetic resonance (NMR) in which an externally applied magnetic field interacts with the nuclei of certain atoms, particularly those of hydrogen (protons). These nuclei possess their own small magnetic fields, similar to those of electrons and the current loops discussed earlier in this chapter.

When placed in an external magnetic field, such nuclei experience a torque that pushes or aligns the nuclei into one of two new energy states—depending on the orientation of its spin (analogous to the N pole and S pole in a bar magnet). Transitions from the lower to higher energy state can be achieved by using an external radio frequency signal to “flip” the orientation of the small magnets. (This is actually a quantum mechanical process. The direction of the nuclear magnetic field is quantized as is energy in the radio waves. We will return to these topics in later chapters.) The specific frequency of the radio waves that are absorbed and reemitted depends sensitively on the type of nucleus, the chemical environment, and the external magnetic field strength. Therefore, this is a resonance phenomenon in which nuclei in a magnetic field act like resonators (analogous to those discussed in the treatment of sound in Oscillatory Motion and Waves) that absorb and reemit only certain frequencies. Hence, the phenomenon is named nuclear magnetic resonance (NMR).

NMR has been used for more than 50 years as an analytical tool. It was formulated in 1946 by F. Bloch and E. Purcell, with the 1952 Nobel Prize in Physics going to them for their work. Over the past two decades, NMR has been developed to produce detailed images in a process now called magnetic resonance imaging (MRI), a name coined to avoid the use of the word “nuclear” and the concomitant implication that nuclear radiation is involved. (It is not.) The 2003 Nobel Prize in Medicine went to P. Lauterbur and P. Mansfield for their work with MRI applications.

The largest part of the MRI unit is a superconducting magnet that creates a magnetic field, typically between 1 and 2 T in strength, over a relatively large volume. MRI images can be both highly detailed and informative about structures and organ functions. It is helpful that normal and non-normal tissues respond differently for slight changes in the magnetic field. In most medical images, the protons that are hydrogen nuclei are imaged. (About 2/3 of the atoms in the body are hydrogen.) Their location and density give a variety of medically useful information, such as organ function, the condition of tissue (as in the brain), and the shape of structures, such as vertebral disks and knee-joint surfaces. MRI can also be used to follow the movement of certain ions across membranes, yielding information on active transport, osmosis, dialysis, and other phenomena. With excellent spatial resolution, MRI can provide information about tumors, strokes, shoulder injuries, infections, etc.

An image requires position information as well as the density of a nuclear type (usually protons). By varying the magnetic field slightly over the volume to be imaged, the resonant frequency of the protons is made to vary with position. Broadcast radio frequencies are swept over an appropriate range and nuclei absorb and reemit them only if the nuclei are in a magnetic field with the correct strength. The imaging receiver gathers information through the body almost point by point, building up a tissue map. The reception of reemitted radio waves as a function of frequency thus gives position information. These “slices” or cross sections through the body are only several mm thick. The intensity of the reemitted radio waves is proportional to the concentration of the nuclear type being flipped, as well as information on the chemical environment in that area of the body. Various techniques are available for enhancing contrast in images and for obtaining more information. Scans called T1, T2, or proton density scans rely on different relaxation mechanisms of nuclei. Relaxation refers to the time it takes for the protons to return to equilibrium after the external field is turned off. This time depends upon tissue type and status (such as inflammation).

While MRI images are superior to x rays for certain types of tissue and have none of the hazards of x rays, they do not completely supplant x-ray images. MRI is less effective than x rays for detecting breaks in bone, for example, and in imaging breast tissue, so the two diagnostic tools complement each other. MRI images are also expensive compared to simple x-ray images and tend to be used most often where they supply information not readily obtained from x rays. Another disadvantage of MRI is that the patient is totally enclosed with detectors close to the body for about 30 minutes or more, leading to claustrophobia. It is also difficult for the obese patient to be in the magnet tunnel. New “open-MRI” machines are now available in which the magnet does not completely surround the patient.

Over the last decade, the development of much faster scans, called “functional MRI” (fMRI), has allowed us to map the functioning of various regions in the brain responsible for thought and motor control. This technique measures the change in blood flow for activities (thought, experiences, action) in the brain. The nerve cells increase their consumption of oxygen when active. Blood hemoglobin releases oxygen to active nerve cells and has somewhat different magnetic properties when oxygenated than when deoxygenated. With MRI, we can measure this and detect a blood oxygen-dependent signal. Most of the brain scans today use fMRI.

Other Medical Uses of Magnetic Fields

Currents in nerve cells and the heart create magnetic fields like any other currents. These can be measured but with some difficulty since their strengths are about [latex]\text{10}^{- 6}[/latex] to [latex]\text{10}^{- 8}[/latex] less than the Earth’s magnetic field. Recording of the heart’s magnetic field as it beats is called a magnetocardiogram (MCG), while measurements of the brain’s magnetic field is called a magnetoencephalogram (MEG). Both give information that differs from that obtained by measuring the electric fields of these organs (ECGs and EEGs), but they are not yet of sufficient importance to make these difficult measurements common.

In both of these techniques, the sensors do not touch the body. MCG can be used in fetal studies, and is probably more sensitive than echocardiography. MCG also looks at the heart’s electrical activity whose voltage output is too small to be recorded by surface electrodes as in EKG. It has the potential of being a rapid scan for early diagnosis of cardiac ischemia (obstruction of blood flow to the heart) or problems with the fetus.

MEG can be used to identify abnormal electrical discharges in the brain that produce weak magnetic signals. Therefore, it looks at brain activity, not just brain structure. It has been used for studies of Alzheimer’s disease and epilepsy. Advances in instrumentation to measure very small magnetic fields have allowed these two techniques to be used more in recent years. What is used is a sensor called a SQUID, for superconducting quantum interference device. This operates at liquid helium temperatures and can measure magnetic fields thousands of times smaller than the Earth’s.

Finally, there is a burgeoning market for magnetic cures in which magnets are applied in a variety of ways to the body, from magnetic bracelets to magnetic mattresses. The best that can be said for such practices is that they are apparently harmless, unless the magnets get close to the patient’s computer or magnetic storage disks. Claims are made for a broad spectrum of benefits from cleansing the blood to giving the patient more energy, but clinical studies have not verified these claims, nor is there an identifiable mechanism by which such benefits might occur.