17.8 Torque on a Current Loop: Motors and Meters
Learning Objectives
By the end of this section, you will be able to:
- Describe how motors and meters work in terms of torque on a current loop.
- Calculate the torque on a current-carrying loop in a magnetic field.
Motors are the most common application of magnetic force on current-carrying wires. Motors have loops of wire in a magnetic field. When current is passed through the loops, the magnetic field exerts torque on the loops, which rotates a shaft. Electrical energy is converted to mechanical work in the process. (See Figure 17.33.)
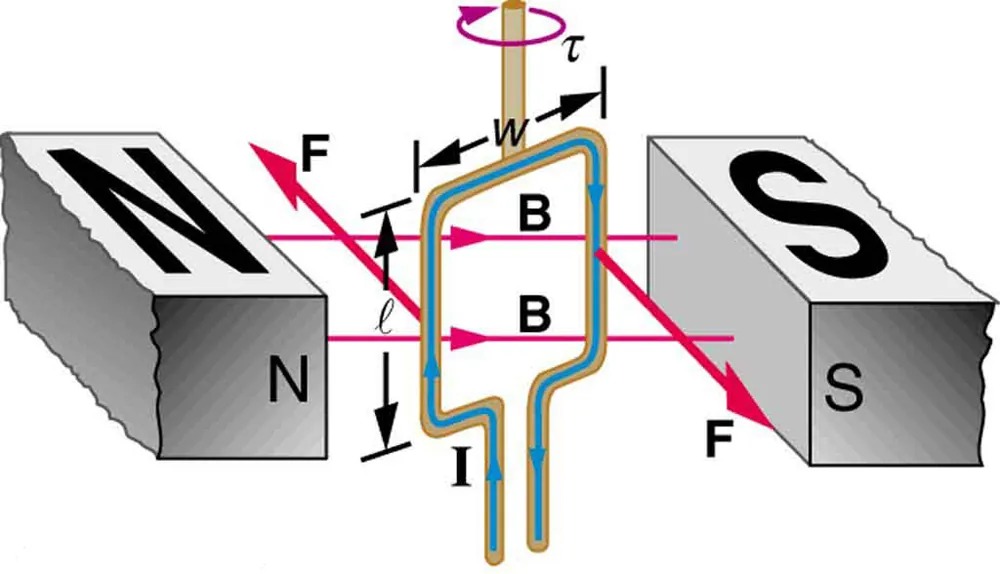
Figure 17.33 Torque on a current loop. A current-carrying loop of wire attached to a vertically rotating shaft feels magnetic forces that produce a clockwise torque as viewed from above. Image from OpenStax College Physics 2e, CC-BY 4.0
Image Description
The image depicts a diagram of a rectangular coil placed between two magnetic poles labeled “N” (North) and “S” (South). The coil is shown with current flowing through it, represented by arrows labeled “I.” The letters “B” indicate the magnetic field lines running horizontally across the coil.
There are forces labeled “F” acting on the coil in opposite directions on each side, illustrating the magnetic force due to the current and the magnetic field. These forces are shown with red arrows perpendicular to the magnetic field lines.
Additional arrows indicate the direction of torque, labeled “τ,” showing a rotational effect on the coil. Dimensions are marked with labels such as “ℓ” for length and “w” for width, indicating the dimensions of the coil.
Let us examine the force on each segment of the loop in Figure 17.33 to find the torques produced about the axis of the vertical shaft. (This will lead to a useful equation for the torque on the loop.) We take the magnetic field to be uniform over the rectangular loop, which has width [latex]w[/latex] and height [latex]l[/latex]. First, we note that the forces on the top and bottom segments are vertical and, therefore, parallel to the shaft, producing no torque. Those vertical forces are equal in magnitude and opposite in direction, so that they also produce no net force on the loop. Figure 17.34 shows views of the loop from above. Torque is defined as [latex]\tau = \text{rF} \text{sin} \theta[/latex], where [latex]F[/latex] is the force, [latex]r[/latex] is the distance from the pivot that the force is applied, and [latex]\theta[/latex] is the angle between [latex]r[/latex] and [latex]F[/latex]. As seen in Figure 17.34(a), right hand rule 1 gives the forces on the sides to be equal in magnitude and opposite in direction, so that the net force is again zero. However, each force produces a clockwise torque. Since [latex]r = w / 2[/latex], the torque on each vertical segment is [latex]\left(\right. w / 2 \left.\right) F \text{sin} \theta[/latex], and the two add to give a total torque.
[latex]\tau = \frac{w}{2} F \text{sin} \theta + \frac{w}{2} F \text{sin} \theta = \text{wF} \text{sin} \theta[/latex]

Figure 17.34 Top views of a current-carrying loop in a magnetic field. (a) The equation for torque is derived using this view. Note that the perpendicular to the loop makes an angle [latex]\theta[/latex] with the field that is the same as the angle between [latex]w / 2[/latex] and [latex]\mathbf{F}[/latex]. (b) The maximum torque occurs when [latex]\theta[/latex] is a right angle and [latex]\text{sin} \theta = 1[/latex]. (c) Zero (minimum) torque occurs when [latex]\theta[/latex] is zero and [latex]\text{sin} \theta = 0[/latex]. (d) The torque reverses once the loop rotates past [latex]\theta = 0[/latex]. Image from OpenStax College Physics 2e, CC-BY 4.0
Image Description
The image consists of a series of diagrams labeled (a) to (d), demonstrating concepts of magnetic force and torque.
(a) A current loop is shown in a magnetic field. The loop is tilted with angle θ. The force (F) is directed perpendicular to the plane of the loop. The torque (τ) is calculated as τ = (w/2)IℓB sin θ, where w is the width, I is the current, ℓ is the length, B is the magnetic field, and θ is the angle.
(b) The current loop is rotated so that θ = 90°, and the forces are again perpendicular with the maximum torque τ = (w/2)IℓB = τmax.
(c) The current loop is shown with θ = 0°. The direction of the magnetic field (B) is aligned with the current, resulting in τ = 0 since θ = 0°.
(d) The loop is shown with a negative angle, resulting in a negative torque. The force (F) is opposite the loop with a negative τ.
Now, each vertical segment has a length [latex]l[/latex] that is perpendicular to [latex]B[/latex], so that the force on each is [latex]F = \text{IlB}[/latex]. Entering [latex]F[/latex] into the expression for torque yields
[latex]\tau = \text{wIlB} \text{sin} \theta .[/latex]
If we have a multiple loop of [latex]N[/latex] turns, we get [latex]N[/latex] times the torque of one loop. Finally, note that the area of the loop is [latex]A = \text{wl}[/latex]; the expression for the torque becomes
[latex]\tau = \text{NIAB} \text{sin} \theta .[/latex]
This is the torque on a current-carrying loop in a uniform magnetic field. This equation can be shown to be valid for a loop of any shape. The loop carries a current [latex]I[/latex], has [latex]N[/latex] turns, each of area [latex]A[/latex], and the perpendicular to the loop makes an angle [latex]\theta[/latex] with the field [latex]B[/latex]. The net force on the loop is zero.
Example 17.5
Calculating Torque on a Current-Carrying Loop in a Strong Magnetic Field
Find the maximum torque on a 100-turn square loop of a wire of 10.0 cm on a side that carries 15.0 A of current in a 2.00-T field.
Strategy
Torque on the loop can be found using [latex]\tau = \text{NIAB} \text{sin} \theta[/latex]. Maximum torque occurs when [latex]\theta = \text{90}º[/latex] and [latex]\text{sin} \theta = 1[/latex].
Solution
For [latex]\text{sin} \theta = 1[/latex], the maximum torque is
[latex]\tau_{\text{max}} = \text{NIAB} .[/latex]
Entering known values yields
[latex]\begin{eqnarray*}\tau_{\text{max}} & = & \left(\text{100}\right) \left(\text{15}.\text{0 A}\right) \left(\text{0}.\text{100} \text{ m}^{2}\right) \left(2 . \text{00 T}\right) \\ & = & \text{30}.\text{0 N} \cdot m.\end{eqnarray*}[/latex]
Discussion
This torque is large enough to be useful in a motor.
The torque found in the preceding example is the maximum. As the coil rotates, the torque decreases to zero at [latex]\theta = 0[/latex]. The torque then reverses its direction once the coil rotates past [latex]\theta = 0[/latex]. (See Figure 17.34(d).) This means that, unless we do something, the coil will oscillate back and forth about equilibrium at [latex]\theta = 0[/latex]. To get the coil to continue rotating in the same direction, we can reverse the current as it passes through [latex]\theta = 0[/latex] with automatic switches called brushes. (See Figure 17.35.)
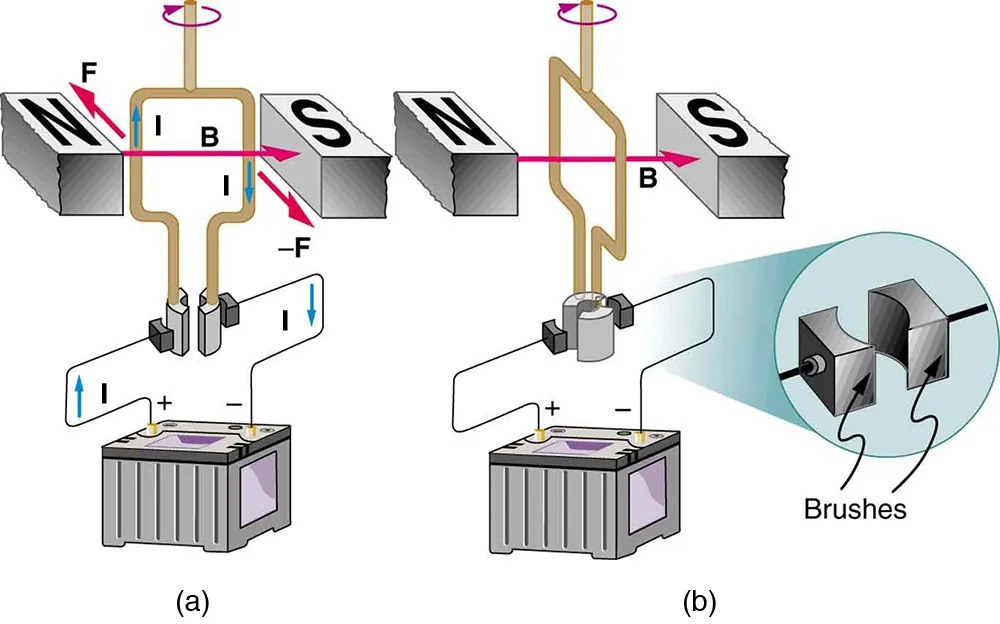
Figure 17.35 (a) As the angular momentum of the coil carries it through [latex]\theta = 0[/latex], the brushes reverse the current to keep the torque clockwise. (b) The coil will rotate continuously in the clockwise direction, with the current reversing each half revolution to maintain the clockwise torque. Image from OpenStax College Physics 2e, CC-BY 4.0
Image Description
The image is a labeled diagram illustrating the functioning of an electric motor using the concept of electromagnetic forces. It has two parts, labeled “(a)” and “(b)”:
(a) The diagram shows a rectangular loop of wire placed between the poles of a permanent magnet labeled “N” (North) and “S” (South). The loop is connected to a battery at the bottom, with wires marked showing the direction of the electrical current (“I”). The current flows in one direction along the vertical parts of the loop but is reversed when it comes out of the battery. There are arrows showing the magnetic field direction (“B”) and the force (“F”) experienced by the loop due to the interaction between the current and the magnetic field. The force is labeled in opposite directions on either side of the loop, illustrating the concept of torque that causes the loop to rotate.
(b) This part of the diagram illustrates the continuation of (a), showing a similar setup but with a focus on the mechanical components of the motor. The loop is connected to a split-ring commutator that reverses the current direction each half turn, allowing for continuous rotation. A zoomed-in view of the commutator and brushes is shown on the right side, highlighting how the brushes maintain contact with the rotating commutator, ensuring the current flows correctly.
Both parts emphasize the combination of electrical input, magnetic field interaction, and mechanical output (rotation), which are crucial for the functioning of an electric motor.
Meters, such as those in analog fuel gauges on a car, are another common application of magnetic torque on a current-carrying loop. Figure 17.36 shows that a meter is very similar in construction to a motor. The meter in the figure has its magnets shaped to limit the effect of [latex]\theta[/latex] by making [latex]B[/latex] perpendicular to the loop over a large angular range. Thus the torque is proportional to [latex]I[/latex] and not [latex]\theta[/latex]. A linear spring exerts a counter-torque that balances the current-produced torque. This makes the needle deflection proportional to [latex]I[/latex]. If an exact proportionality cannot be achieved, the gauge reading can be calibrated. To produce a galvanometer for use in analog voltmeters and ammeters that have a low resistance and respond to small currents, we use a large loop area [latex]A[/latex], high magnetic field [latex]B[/latex], and low-resistance coils.
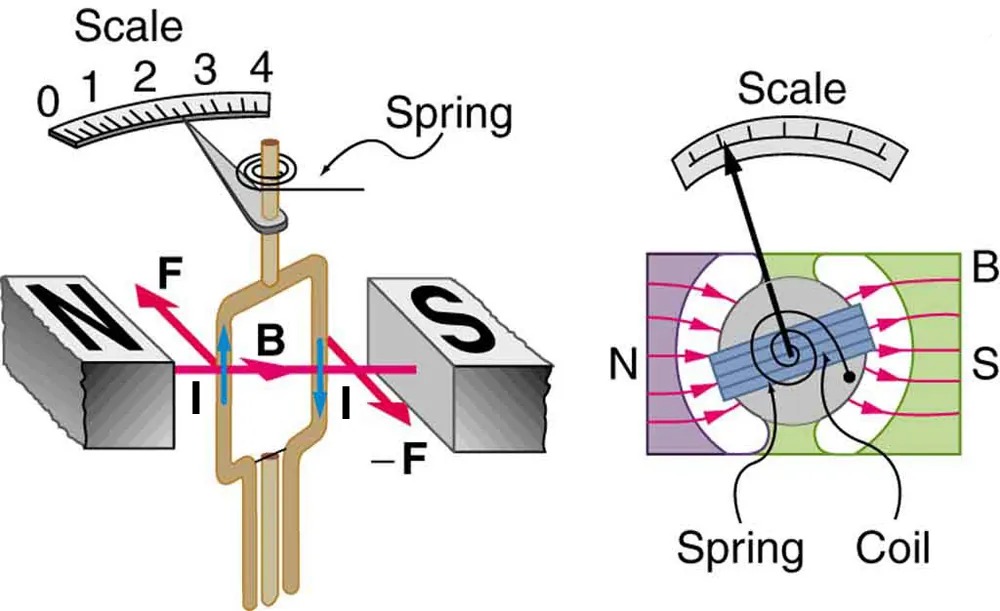
Figure 17.36 Meters are very similar to motors but only rotate through a part of a revolution. The magnetic poles of this meter are shaped to keep the component of [latex]B[/latex] perpendicular to the loop constant, so that the torque does not depend on [latex]\theta[/latex] and the deflection against the return spring is proportional only to the current [latex]I[/latex]. Image from OpenStax College Physics 2e, CC-BY 4.0
Image Description
The image contains two schematic diagrams illustrating components of a galvanometer.
Left Diagram: This section shows a partial side view of a galvanometer. From left to right, there is a block labeled “N” representing the North pole of a magnet, and a block labeled “S” representing the South pole. Between these poles, a rectangular coil is depicted, labeled “B” and “I”. Red arrows point rightward through “B” from “N” to “S”, indicating the direction of magnetic force and current flow. Blue arrows labeled “I” indicate current direction within the coil. The coil is suspended on a spring, connecting it to a scale, which is labeled from 0 to 4. The scale pointer is shown pointing to a position between 2 and 3, with a spring attached near the top.
Right Diagram: This section shows a top view of a similar setup. Blocks labeled “N” and “S” are shown with a coil in between, similar to the left diagram. Curved, pink arrows within the coil represent the magnetic field lines emanating from the North to the South. A spring connected to the coil is visible, along with a scale marked from 0 to 4. The pointer indicates a position near the middle of the scale. The labels “B”, “Spring”, and “Coil” describe the components.

