Chapitre 7 : Sémantique
7.12 Introduction à la théorie des ensembles
Un ou plusieurs éléments interactifs ont été exclus de cette version du texte. Vous pouvez les consulter en ligne ici, mais notez que le contenu est en anglais : https://ecampusontario.pressbooks.pub/essentialsoflinguistics2/?p=827#oembed-1
Nous venons de présenter la dénotation comme un angle de réflexion sur la signification linguistique. Prenons le mot ;chat. Le sens de ce mot serait le sens de ;chat que vous stockez dans votre lexique mental, mais sa dénotation serait l’ensemble des chats dans le monde réel. D’un point de vue terminologique, les « choses » qui font partie d’un ensemble sont appelées membres (ou éléments) de cet ensemble. Comme nous l’avons expliqué dans la section précédente, les doubles crochets signifient « la dénotation de (l’expression linguistique) ». Ainsi, le mot ⟦chat⟧ dans la phrase (1) doit être lu comme « la dénotation de l’expression linguistique chat ». ;
| (1) | ⟦chat⟧ = l’ensemble des chats dans le monde réel |
Rappelons également que les noms dénotent la personne qu’ils désignent. Ainsi, le nom Panks, le surnom de mon chat, dénote l’individu (le chat) nommé Panks dans le monde réel (le chat au premier plan dans la figure 7.16).
| (2) | ⟦ Panks ⟧ = l’individu Panks dans le monde réel |
;

Les phrases dénotent la ;valeur de vérité de la phrase qui peut également être exprimée comme une condition de vérité. Le fait de réfléchir au sens des prédicats intransitifs comme chat sous la forme d’ensembles de choses constitue un moyen intuitif de caractériser la condition de vérité d’une phrase comme Panks est un chat. Cette phrase est vraie si l’individu Panks fait partie de l’ensemble des chats du monde réel.
| (3) | ⟦ Panks est un chat ⟧ = V si l’individu Panks est membre de l’ensemble des chats dans le monde réel, F si ce n’est pas le cas. |
Puisque Panks est effectivement un chat, la phrase (3) dénoterait la valeur de vérité V. Par ailleurs, si ;Karti ;est le nom d’un chien (voir la figure 7.17), l’exemple (4) serait la dénotation de la phrase Karti est un chat. L’exemple dénoterait F cette fois, car Karti ne fait pas partie de l’ensemble des chats de notre monde.
| (4) | ⟦ Karti est un chat ⟧ = V si l’individu Karti est membre de l’ensemble des chats dans le monde réel, F si ce n’est pas le cas. |

La figure 7.18 illustre le concept d’appartenance à un ensemble. Supposons que nous vivons dans un monde où les animaux énumérés sont les seuls à exister. Le cercle supérieur représente l’ensemble des chats de ce monde. Le cercle du bas représente l’ensemble des chiens de ce monde. La phrase « Panks est un chat » exprime la relation d’appartenance à un ensemble de Panks dans ce monde : Panks est un membre dans le cercle supérieur. Si ;la phrase « Karti est un chat » est fausse, c’est parce que Karti n’apparaît pas dans ce cercle (il est cependant dans l’ensemble des chiens).
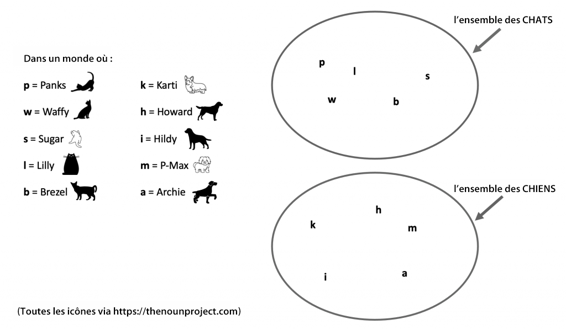
Un ensemble peut contenir des ensembles plus petits. En d’autres mots, l’ensemble des chats de la figure 7.19 pourrait inclure un sous-groupe de chats qui ont une certaine propriété en commun. Par exemple, admettons que Panks, Waffy et Lilly sont des chats sibériens, et que Sugar et Brezel ne le sont pas. Nous pouvons affirmer que l’ensemble contenant uniquement Panks, Waffy et Lilly est un sous-ensemble de l’ensemble des chats.
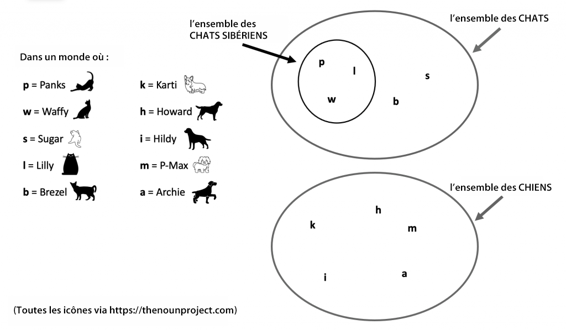
Voici une définition plus formelle de la relation de sous-ensemble : utilisons les variables A et B pour représenter des ensembles (les lettres majuscules sont généralement utilisées pour les variables et les constantes qui représentent un ensemble).
| (5) | A est un sous-ensemble de B si tous les membres de A sont également membres de B. |
Comme vous pouvez le constater, Panks, Waffy et Lilly font partie de l’ensemble des chats sibériens. Panks, Waffy et Lilly font également partie de l’ensemble des chats. Par conséquent, l’ensemble des chats sibériens est un sous-ensemble de l’ensemble des chats. ;En logique, le symbole du sous-ensemble est ⊆. A⊆B peut être lu comme suit : « A est un sous-ensemble de B ». Ainsi, dans notre exemple, si nous appelons l’ensemble des chats C et l’ensemble des chats sibériens S, la relation de sous-ensemble peut être énoncée comme suit : S⊆C.
Dans la définition donnée au point (5), nous pouvons aussi dire que B est un ;surensemble de A. Dans notre exemple, l’ensemble des chats est un surensemble de l’ensemble des chats sibériens. Le symbole du surensemble est simplement le symbole du sous-ensemble inversé. Ainsi, C⊇S se lit comme suit : « C est un surensemble de S ».
Selon la définition du point (5), cela signifie également que si A et B contenaient exactement les mêmes membres, A serait toujours un sous-ensemble de B et vice versa. Si nous voulons nommer le fait que certains membres de B sont ;absents de A (c’est-à-dire que tous les chats ne sont pas des chats sibériens dans la figure 7.19), nous utilisons le terme sous-ensemble propre. Le point (6) est la définition formelle de ;sous-ensemble propre.
| (6) | A est un sous-ensemble ; propre de B si tous les membres de A sont également membres de B, et s’il existe au moins un membre de B qui n’est pas membre de A. |
Ainsi, dans la figure 7.19, S est un sous-ensemble de C, mais S est également un sous-ensemble propre de C. Le symbole du sous-ensemble propre est ⊂ : nous pouvons donc écrire S⊂C. Nous pouvons aussi affirmer que B est un sur-ensemble propre de A dans la définition fournie au point (6). Le symbole du surensemble est ⊃, nous pouvons donc écrire C⊃S pour notre exemple de la figure 7.19.
Les symboles utilisés ici proviennent d’une branche des mathématiques qui étudie les ensembles, appelée théorie des ensembles. Le tableau 1 ci-dessous résume certaines des notations courantes de la théorie des ensembles.
Tableau 7.1. Notation de la théorie des ensembles
| Notation | Sens |
| A | L’ensemble A. Les lettres majuscules sont utilisées pour désigner les ensembles. |
| {a, b, c } | L’ensemble contenant les membres a, b et c. |
| b ∈ A | b est membre de A. |
| d ∉ A | d n’est pas membre de A. |
| A⊆B | A est un sous-ensemble de B. |
| B⊂A | B est un surensemble de A. |
| A⊂B | A est un sous-ensemble propre de B. |
| B⊂A | B est un sur-ensemble propre de A. |
| A = B | A est identique à B (c’est-à-dire que A et B ont exactement les mêmes membres). |
| |A| | La cardinalité de A. C’est-à-dire le nombre de membres de A. |
| |A| = 3 | La cardinalité de A est égale à 3. C’est-à-dire qu’il y a trois membres dans A. |
| A∩B | L’intersection de A et B. Cet ensemble contient des objets qui sont à la fois membres de A et membres de B. |
| A∪B | L’union de A et B. Cet ensemble contient des objets qui sont soit membres de A, soit membres de B. |
;
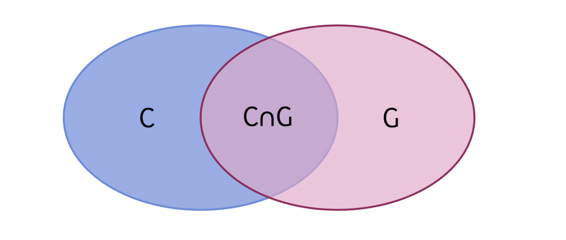
La théorie des ensembles est utile pour comprendre comment le sens de certains mots quantificatifs intervient dans la langue. Quantificatif signifie « lié à la quantité » ou « au volume » de quelque chose. En anglais, il existe des déterminants quantificatifs comme every, some, most, many, ;few, ;two, five, etc. Pour comprendre le sens d’une phrase comme ;« Two cats are grey ;», penchons-nous sur les ;intersections d’ensembles. Disons qu’il existe un ensemble des chats (appelons-le C). Supposons qu’il existe un autre ensemble, un ensemble de choses grises (appelons-le G). L’intersection (ou le chevauchement) de C et de G est l’ensemble des chats gris (voir figure 7.20). Nous pouvons écrire pour cet ensemble C∩G selon la notation de la théorie des ensembles.
;
Le déterminant quantificatif two pose essentiellement la question suivante : « Combien de choses se trouvent dans l’intersection C∩G? ». Le déterminant two signifie ;« deux choses ». Penchons-nous maintenant sur ;every : Que signifie ;« Every cat is grey » du point de vue des ensembles? Cela signifie que tout ce qui se trouve dans l’ensemble des chats, C, se trouve également dans l’ensemble des chats gris, G. La notation formelle de la théorie des ensembles n’est pas très importante dans le présent manuel – tout ce que vous devez retenir pour la section suivante est ce qui constitue un surensemble et un sous-ensemble d’un point de vue conceptuel. Nous invitons les apprenants avancés à effectuer les exercices à la fin de cette section pour vérifier si vous pouvez écrire ;« Panks est un chat », « Deux chats sont gris », et « Tous les chats sont gris » dans la notation de la théorie des ensembles!
Vérifiez votre compréhension
Un élément interactif H5P a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici, mais notez que le contenu est en anglais :
https://ecampusontario.pressbooks.pub/essentialsoflinguistics2/?p=827#h5p-74
Références
Gamut, L. T. F. (1991). ;Logic, Language and Meaning Vol. 1. University of Chicago Press.

