7.4 Équation des ondes
L’équation des ondes modélise la propagation des ondes, telles que les ondes sonores, les ondes lumineuses ou les ondes aquatiques, à travers un milieu. Elle rend compte de la façon dont ces ondes se déplacent et changent dans le temps et dans l’espace. L’équation des ondes pour le problème de valeur initiale aux limites portant sur le déplacement (déflexion) d’une corde qui vibre et dont les extrémités sont maintenues fixes est
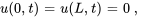
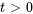
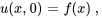
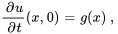
En utilisant la méthode de séparation des variables, on trouve la solution formelle de ce problème de valeur initiale aux limites :
où
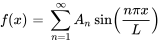 et
et 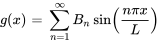
sont les séries sinusoïdales de Fourier de 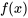 et
et 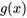 sur
sur ![[0,L] [0,L]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/f735caea0d128c5937b57c7ef8a1e6cb.png) et
et
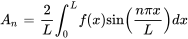 et
et 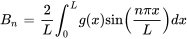
Trouver la solution au problème de la corde qui vibre
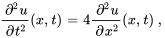
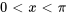 ,
, 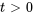
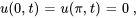
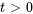
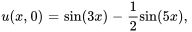
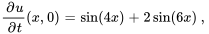
Afficher/Masquer la solution
En comparant l’équation à l’équation 7.4.1, on observe que 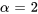 ,
, 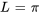 ,
, 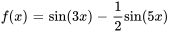 et que
et que 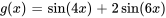 . Comme
. Comme 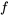 et
et  sont exprimés en termes de fonctions sinusoïdales, il est possible de déterminer les valeurs des coefficients
sont exprimés en termes de fonctions sinusoïdales, il est possible de déterminer les valeurs des coefficients 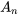 et
et 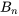 en transformant
en transformant 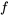 et
et  en
en 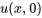 et
et 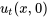 , respectivement.
, respectivement.
En remplaçant 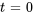 dans l’équation 7.4.2, on obtient
dans l’équation 7.4.2, on obtient
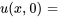
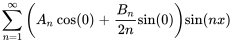
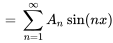
À partir des valeurs initiales aux limites, on a
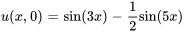
Par conséquent,
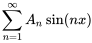
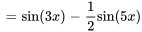
En égalisant les coefficients des termes similaires, on constate que
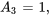 et
et 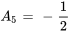
tandis que les coefficients restants sont nuls. De même, en différenciant partiellement l’équation de la section 7.4.2 par rapport à  et en substituant
et en substituant 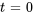 , on obtient
, on obtient
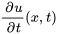

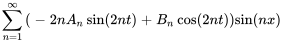
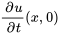

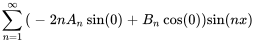
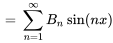
À partir des valeurs initiales aux limites, on a
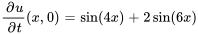
Par conséquent,
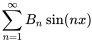
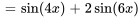
En égalisant les coefficients des termes similaires, on constate que
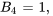 et
et 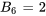
tandis que les coefficients restants sont nuls.
La solution du problème est donc
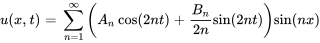
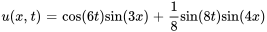
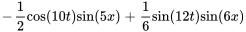
La figure représente 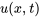 sous forme schématique.
sous forme schématique.
Prenons un exemple
Section 7.4 Exercices
- Trouve la solution au problème de valeur initiale aux limites décrivant des ondes
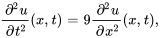
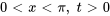
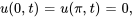
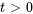
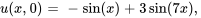
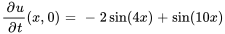
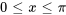
Afficher/Masquer la réponse
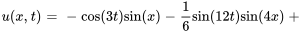
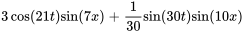
- Trouve la solution au problème de valeur initiale aux limites décrivant des ondes
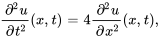
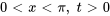
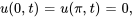
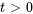
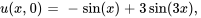
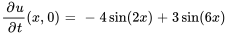
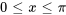
Afficher/Masquer la réponse
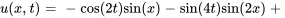
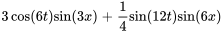

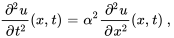
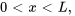
![u(x,t) = somme_(n = 1)^oo[A_n cos((npialphat) / L) + (B_nL) / (npialpha)sin((npialphat) / L )] u(x,t) = somme_(n = 1)^oo[A_n cos((npialphat) / L) + (B_nL) / (npialpha)sin((npialphat) / L )]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/8546d96f1d4f63ab70c10f4412a15fc8.png)