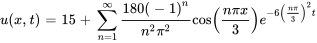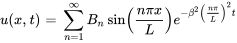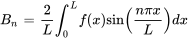7.3 Équation de la chaleur
A. Introduction à la résolution d’équations différentielles partielles
Cette section aborde la méthode de séparation des variables pour résoudre des équations différentielles partielles couramment rencontrées en physique mathématique, telles que les équations de la chaleur et des ondes. Cette méthode simplifie les équations différentielles partielles complexes en équations différentielles ordinaires plus faciles à gérer. Bien que les algorithmes informatiques tels que les différences finies et les éléments finis soient fréquemment employés pour résoudre des équations différentielles partielles, leur précision peut être difficile à évaluer. C’est pourquoi la méthode analytique de séparation des variables est importante pour vérifier les résultats de ces méthodes de calcul.
B. Équation de la chaleur
L’équation de la chaleur décrit la diffusion de la chaleur dans un milieu au fil du temps. Elle est formulée en considérant un élément de petit volume à l’intérieur du matériau, où le taux de variation d’énergie thermique est égal au flux de chaleur net. En représentant la température au point et à l’instant
et à l’instant  par
par 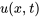 , l’équation de la chaleur en une dimension peut être exprimée sous la forme
, l’équation de la chaleur en une dimension peut être exprimée sous la forme
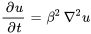
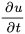 représente le taux de variation de la température dans le temps,
représente le taux de variation de la température dans le temps, 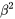 (où
(où 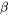 est la diffusivité thermique du matériau) est une constante qui combine la conductivité thermique, la densité et la capacité thermique spécifique du matériau et
est la diffusivité thermique du matériau) est une constante qui combine la conductivité thermique, la densité et la capacité thermique spécifique du matériau et 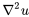 (le laplacien de
(le laplacien de 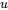 ) représente la divergence du gradient de température, indiquant comment la température change dans l’espace autour de n’importe quel point. Dans une dimension, comme une simple tige, le laplacien de
) représente la divergence du gradient de température, indiquant comment la température change dans l’espace autour de n’importe quel point. Dans une dimension, comme une simple tige, le laplacien de 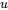 est simplifié en
est simplifié en  . L’équation de la chaleur devient donc
. L’équation de la chaleur devient donc 
Pour résoudre cette équation, il faut définir des conditions aux limites et des conditions initiales. La condition initiale spécifie la distribution de la température dans tout le domaine au moment initial, généralement 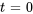 . Par exemple, pour une tige ou un domaine unidimensionnel similaire, la condition initiale peut être
. Par exemple, pour une tige ou un domaine unidimensionnel similaire, la condition initiale peut être 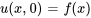 , où
, où 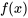 décrit la distribution de la température le long de la tige au moment initial.
décrit la distribution de la température le long de la tige au moment initial.
C. Solution de l’équation de la chaleur avec des conditions aux limites de Dirichlet
Prenons une tige uniforme d’une longueur 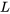 dont les deux extrémités sont maintenues à une température nulle constante. L’équation de la chaleur en une dimension est
dont les deux extrémités sont maintenues à une température nulle constante. L’équation de la chaleur en une dimension est
Pour une température nulle aux deux extrémités de la tige, les conditions aux limites sont
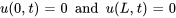
La distribution initiale de la température le long de la tige est donnée par
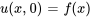
En utilisant la méthode de séparation des variables, on suppose que la solution peut être écrite comme le produit de deux fonctions, l’une dépendant uniquement de 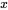 et l’autre uniquement de
et l’autre uniquement de  .
.
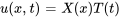
En substituant la forme de la solution dans l’équation de la chaleur, on obtient
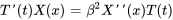
En divisant l’équation par 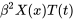 , on trouve
, on trouve
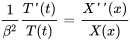
Cette équation est scindée en deux équations différentielles ordinaires (EDO) parce que le côté gauche dépend uniquement de  et le côté droit uniquement de
et le côté droit uniquement de 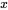 . Pour que cette équation soit valable pour toutes les valeurs de
. Pour que cette équation soit valable pour toutes les valeurs de 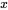 et
et  , chacun des côtés de l’équation doit être indépendamment égal à une constante. En effet, la seule façon pour qu’une fonction de
, chacun des côtés de l’équation doit être indépendamment égal à une constante. En effet, la seule façon pour qu’une fonction de 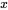 soit égale à une fonction de
soit égale à une fonction de  en toutes circonstances est que les deux soient égales à la même valeur constante. Par conséquent, on définit pour les deux côtés de l’équation une constante négative, notée
en toutes circonstances est que les deux soient égales à la même valeur constante. Par conséquent, on définit pour les deux côtés de l’équation une constante négative, notée 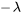 ,
, 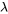 devenant ainsi la constante de séparation. Par convention, le signe négatif est ajouté pour simplifier les étapes suivantes.
devenant ainsi la constante de séparation. Par convention, le signe négatif est ajouté pour simplifier les étapes suivantes.
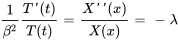
On obtient donc deux EDO distinctes.

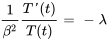
Résolution de l’EDO spatiale
Pour résoudre la partie spatiale de l’équation différentielle ordinaire (EDO), il faut d’abord réarranger l’équation
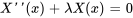
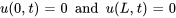
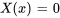 est la solution triviale à ce problème de conditions aux limites. Toutefois, nous nous intéressons ici aux solutions non triviales, car elles fournissent des indications utiles sur le comportement du système dans diverses conditions. Une valeur de
est la solution triviale à ce problème de conditions aux limites. Toutefois, nous nous intéressons ici aux solutions non triviales, car elles fournissent des indications utiles sur le comportement du système dans diverses conditions. Une valeur de 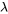 pour laquelle ce problème a une solution non triviale est appelée valeur propre du problème et les solutions son triviales sont les fonctions propres associées à ce
pour laquelle ce problème a une solution non triviale est appelée valeur propre du problème et les solutions son triviales sont les fonctions propres associées à ce 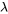 . Ces fonctions propres, contrairement à la solution triviale, permettent de mieux comprendre la dynamique et les caractéristiques du système.
. Ces fonctions propres, contrairement à la solution triviale, permettent de mieux comprendre la dynamique et les caractéristiques du système.
Trouver les valeurs propres et les fonctions propres
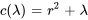 . En fonction du signe de
. En fonction du signe de 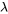 , il y a trois cas à considérer.
, il y a trois cas à considérer.Cas n° 1 : 
Dans ce cas, les racines de 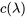 sont complexes et la solution est
sont complexes et la solution est
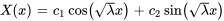
En appliquant les premières conditions aux limites 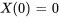 , on trouve
, on trouve 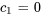 . En appliquant les deuxièmes conditions aux limites
. En appliquant les deuxièmes conditions aux limites 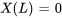 , on obtient l’équation
, on obtient l’équation 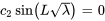 . Pour obtenir une solution non triviale, la fonction sinusoïdale doit elle-même être nulle.
. Pour obtenir une solution non triviale, la fonction sinusoïdale doit elle-même être nulle.
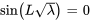

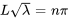 for
for 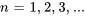
Par conséquent, les valeurs propres positives et leurs fonctions propres associées de ce problème aux limites sont
 pour
pour 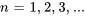
Cas n° 2 : 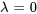
En ce cas, la solution générale de l’équation différentielle est
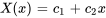
En appliquant les premières conditions aux limites 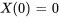 , on trouve
, on trouve 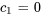 . En appliquant les deuxièmes conditions aux limites
. En appliquant les deuxièmes conditions aux limites 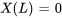 , on obtient
, on obtient  . Dans ce cas, la seule solution est la solution triviale, qui est rejetée.
. Dans ce cas, la seule solution est la solution triviale, qui est rejetée.
Cas n° 3 : ![]()
Dans ce cas, les racines de 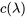 sont un nombre réel, ce qui donne la solution
sont un nombre réel, ce qui donne la solution
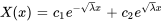
En appliquant les premières conditions aux limites 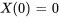 , on trouve
, on trouve 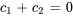 . Les deuxièmes conditions aux limites
. Les deuxièmes conditions aux limites 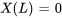 donnent
donnent 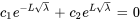 . En résolvant le système pour
. En résolvant le système pour 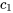 et
et 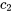 , on obtient
, on obtient
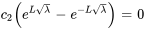
Comme on cherche une solution non triviale, le terme entre parenthèses doit être nul.
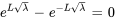
Cependant, cette équation n’est valable que si 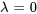 , ce qui contredit notre hypothèse
, ce qui contredit notre hypothèse 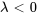 . On conclut donc que
. On conclut donc que 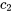 doit être égal à zéro, ce qui donne une solution triviale.
doit être égal à zéro, ce qui donne une solution triviale.
Par conséquent, les seules valeurs et fonctions propres valables pour la partie spatiale de l’équation sont réalisées lorsque  . Elles sont données par
. Elles sont données par
 pour
pour 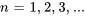
Résolution de l’EDO temporelle
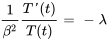
et substituer les valeurs propres précédemment déterminées 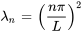 , ce qui transforme l’EDO temporelle en
, ce qui transforme l’EDO temporelle en

Pour chaque valeur propre 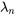 , la solution à cette équation différentielle est
, la solution à cette équation différentielle est
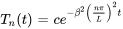 pour
pour 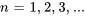
où  représente une constante arbitraire. La série de fonctions
représente une constante arbitraire. La série de fonctions 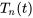 décrit l’évolution de la température dans le temps pour chaque mode spatial
décrit l’évolution de la température dans le temps pour chaque mode spatial 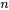 .
.
Construction de la solution générale
Pour construire la solution générale de l’équation de la chaleur, on combine la solution spatiale et la solution temporelle en une série composite.
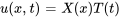
Étant donné les solutions 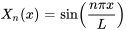 et
et 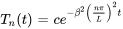 , la forme combinée pour chaque mode
, la forme combinée pour chaque mode 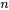 est
est
 pour
pour 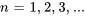
Notée en série, elle devient
où la constante  de la solution temporelle est représentée par
de la solution temporelle est représentée par 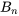 pour chaque
pour chaque 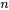 , car cette constante peut varier avec chaque terme de la série. Pour trouver le coefficient
, car cette constante peut varier avec chaque terme de la série. Pour trouver le coefficient 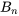 , on applique la condition initiale
, on applique la condition initiale 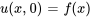 . Ce qui donne
. Ce qui donne
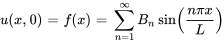
Il s’agit de la représentation en série sinusoïdale de Fourier de 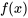 sur l’intervalle
sur l’intervalle ![[0,L] [0,L]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/f735caea0d128c5937b57c7ef8a1e6cb.png) . Les coefficients
. Les coefficients 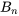 sont déterminés par
sont déterminés par
Trouver la solution au problème de valeur initiale aux limites décrivant un flux thermique
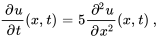
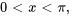
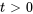
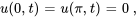
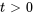
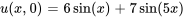
Afficher/Masquer la solution
En comparant l’équation différentielle partielle à l’équation de la section 7.3.1, on observe que 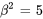 et
et 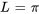 . Étant donné que la condition initiale est une combinaison linéaire de quelques fonctions sinusoïdales (fonctions propres), il suffit simplement de trouver la combinaison de termes dans la solution générale de la section 7.3.2 satisfaisant la condition initiale
. Étant donné que la condition initiale est une combinaison linéaire de quelques fonctions sinusoïdales (fonctions propres), il suffit simplement de trouver la combinaison de termes dans la solution générale de la section 7.3.2 satisfaisant la condition initiale 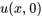 .
.
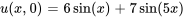
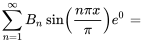
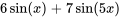
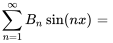
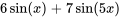
D’après l’argument des fonctions sinus, les deux termes correspondent respectivement à 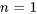 et
et 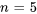 . De même,
. De même, 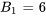 et
et 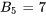 . Tous les autres coefficients sont nuls.
. Tous les autres coefficients sont nuls.
La solution du problème de flux thermique est donc
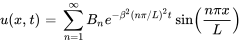
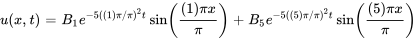
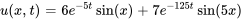
Prenons un exemple
Trouver la solution au problème de valeur initiale aux limites décrivant un flux thermique
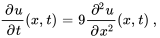
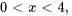
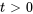
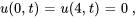
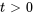
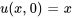
Afficher/Masquer la solution
En comparant l’équation à l’équation 7.3.1, on observe que  ,
, 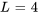 et
et 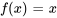 . Contrairement à l’exemple précédent, la fonction de condition initiale n’est pas similaire aux fonctions propres (fonctions sinusoïdales). Par conséquent, il faut d’abord trouver
. Contrairement à l’exemple précédent, la fonction de condition initiale n’est pas similaire aux fonctions propres (fonctions sinusoïdales). Par conséquent, il faut d’abord trouver 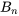 avec l’équation 7.3.3.
avec l’équation 7.3.3.
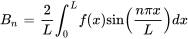
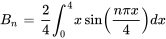
Avec l’intégration par parties, on a
![B_n = [-2 / (npi)xcos((npix) / 4)]_0^4 + 2 / (npi)int_0^4cos((npix) / 4)dx B_n = [-2 / (npi)xcos((npix) / 4)]_0^4 + 2 / (npi)int_0^4cos((npix) / 4)dx](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/ee57ec804bc06cf6795e24a20e6da4f6.png)
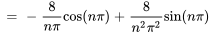
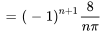
La solution est donc
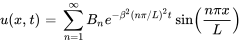
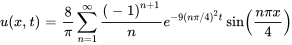
La figure ci-dessous montre la somme partielle de la solution 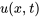 .
.
Prenons un exemple
D. Solution de l’équation de la chaleur avec des conditions aux limites de Neumann
Les conditions aux limites de Neumann spécifient la valeur de la dérivée (gradient) de la température à la limite, représentant souvent des surfaces isolées ou adiabatiques où il n’y a pas de flux de chaleur. Par exemple,  peut représenter une extrémité de la tige parfaitement isolée.
peut représenter une extrémité de la tige parfaitement isolée.
Pour développer une solution pour l’équation de la chaleur avec des conditions aux limites de Neumann, on utilise la méthode de séparation des variables.
Prenons une tige uniforme de longueur 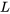 dont les deux extrémités sont parfaitement isolées (aucun flux de chaleur n’entre dans la tige ou n’en sort) et dont la température aux deux extrémités est maintenue constante. L’équation de la chaleur en une dimension est
dont les deux extrémités sont parfaitement isolées (aucun flux de chaleur n’entre dans la tige ou n’en sort) et dont la température aux deux extrémités est maintenue constante. L’équation de la chaleur en une dimension est
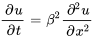
Pour les extrémités isolées, la dérivée (gradient) de la température à la limite est zéro. Les conditions aux limites de Neumann sont donc

La distribution initiale de la température le long de la tige est donnée par
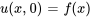
La solution de ce problème aux limites est
où
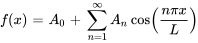
est la série cosinusoïdale de Fourier de 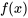 sur
sur ![[0,L] [0,L]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/f735caea0d128c5937b57c7ef8a1e6cb.png) et les coefficients
et les coefficients 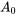 et
et  sont donnés par
sont donnés par
Trouver la solution au problème de valeur initiale aux limites décrivant un flux thermique
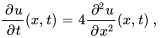
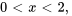
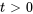
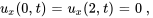
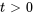
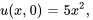
Afficher/Masquer la solution
En comparant l’équation à l’équation 7.3.1, on observe que 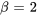 ,
, 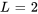 et
et 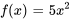 . Il faut d’abord trouver les coefficients
. Il faut d’abord trouver les coefficients 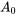 et
et  . On utilise l’équation de la section 7.3.5.
. On utilise l’équation de la section 7.3.5.
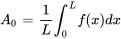
![A_0 = frac int_{0}^ 5x^2 dx = 5 / 2[x^3 / 3]_0^2 = 20 / 3 A_0 = frac int_{0}^ 5x^2 dx = 5 / 2[x^3 / 3]_0^2 = 20 / 3](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/b3c92d3b38819686132c35076eca2b63.png)
On applique l’équation de la section 7.3.6 pour trouver  .
.
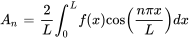
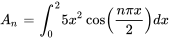
Avec l’intégration par parties, on a
![= [(10x^2) / (npi)sin((npix) / 2)]_0^2-20 / (npi) int_0^2 xsin((npix) / 2 ) dx = [(10x^2) / (npi)sin((npix) / 2)]_0^2-20 / (npi) int_0^2 xsin((npix) / 2 ) dx](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/1c3b94bc15cfde4dfc909658aedf905f.png)
![= [(10x^2) / (npi)sin((npix) / 2)-80 / (npi)^3((-npi) / 2xcos((npix) / 2) + sin((npix) / 2))]_0^2 = [(10x^2) / (npi)sin((npix) / 2)-80 / (npi)^3((-npi) / 2xcos((npix) / 2) + sin((npix) / 2))]_0^2](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/7b1ebbcc1eae671412e5fd99aaab1920.png)

Étant donné que 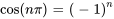 ,
,  est simplifié en
est simplifié en

La solution générale est donc donnée par l’équation de la section 7.3.4


La figure ci-dessous montre la somme partielle de la solution 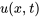 .
.
Prenons un exemple
Section 7.3 Exercices
- Trouver la solution au problème de valeur initiale aux limites décrivant un flux thermique
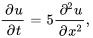
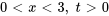
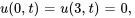
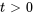
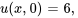
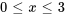
Afficher/Masquer la réponse
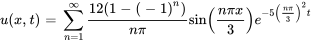
- Trouver la solution au problème de valeur initiale aux limites décrivant un flux thermique
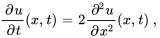
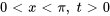
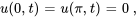
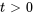
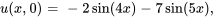
Afficher/Masquer la réponse
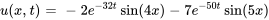
- Trouver la solution au problème de valeur initiale aux limites décrivant un flux thermique
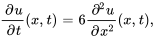
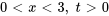
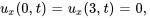
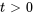
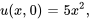
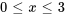
Afficher/Masquer la réponse