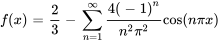7.2 Série de Fourier
Pour résoudre des équations différentielles partielles, on emploie souvent une méthode qui transforme les équations différentielles partielles complexes en équations différentielles ordinaires plus simples. Une étape clé de cette méthode consiste à exprimer les fonctions sous forme de séries de Fourier trigonométriques. Cette section donne donc un bref aperçu des séries de Fourier, ce qui nous permettra d’aborder efficacement la résolution des équations différentielles partielles dans les sections suivantes.
A. Série de Fourier
Une série de Fourier est une expansion d’une fonction 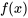 en termes d’une somme infinie de sinus et de cosinus. La série permet d’exprimer une forme d’onde périodique complexe comme une combinaison de fonctions oscillantes simples.
en termes d’une somme infinie de sinus et de cosinus. La série permet d’exprimer une forme d’onde périodique complexe comme une combinaison de fonctions oscillantes simples.
Décomposition en sinus et cosinus
La formule pour une série de Fourier d’une fonction 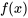 définie dans l’intervalle
définie dans l’intervalle 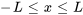 est
est
![f(x) = a_0 + somme_{n = 1}^{infty} [a_n cos(frac{npi x}{L}) + b_n sin(frac{npi x}{L})] f(x) = a_0 + somme_{n = 1}^{infty} [a_n cos(frac{npi x}{L}) + b_n sin(frac{npi x}{L})]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/8c13e408d45e96ba59b43f35c374f63a.png)
où 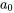 ,
, 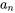 et
et 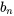 sont les coefficients de Fourier qui déterminent la grandeur des termes correspondants en sinus et en cosinus. Ils sont calculés comme suit :
sont les coefficients de Fourier qui déterminent la grandeur des termes correspondants en sinus et en cosinus. Ils sont calculés comme suit :
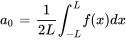
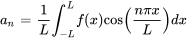 pour
pour 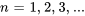
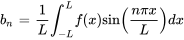 pour
pour 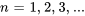
B. Série de Fourier de sinus et de cosinus
Dans certains cas, la fonction 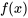 peut avoir des symétries spécifiques, qui simplifient la série de Fourier :
peut avoir des symétries spécifiques, qui simplifient la série de Fourier :
Série de sinus : si 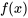 est une fonction impaire (à savoir
est une fonction impaire (à savoir 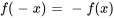 ), les termes en cosinus de la série de Fourier disparaissent et seules les termes en sinus subsistent. Il s’ensuit une série de sinus, qui est particulièrement utile pour les fonctions définies sur des intervalles symétriques et satisfaisant certaines conditions aux limites, comme la nullité aux extrémités.
), les termes en cosinus de la série de Fourier disparaissent et seules les termes en sinus subsistent. Il s’ensuit une série de sinus, qui est particulièrement utile pour les fonctions définies sur des intervalles symétriques et satisfaisant certaines conditions aux limites, comme la nullité aux extrémités.
Série de cosinus : si 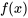 est une fonction paire (à savoir
est une fonction paire (à savoir 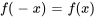 ), les termes en sinus disparaissent, ne laissant que les termes en cosinus. La série de cosinus obtenue est utile pour les problèmes dans lesquels la dérivée de
), les termes en sinus disparaissent, ne laissant que les termes en cosinus. La série de cosinus obtenue est utile pour les problèmes dans lesquels la dérivée de 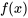 est nulle aux extrémités.
est nulle aux extrémités.
Les séries de Fourier font partie intégrante de la résolution des EDP, en particulier lorsque l’on utilise la méthode de séparation des variables. Cette méthode exige souvent que les conditions aux limites soient satisfaites, ce qui est possible avec la série de Fourier. En exprimant une fonction sous la forme d’une série de Fourier, les EDP peuvent être transformées en EDO plus simples, chacune associée à une composante de fréquence différente de la fonction d’origine.
Trouver la série de Fourier Series de 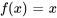 sur
sur ![[-2,2] [-2,2]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/ef8463565c3162f8ddceeb520d873307.png) .
.
Afficher/Masquer la solution
L’extrémité 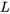 est 2. La série de Fourier est donc
est 2. La série de Fourier est donc
![f(x) = a_0 + somme_{n = 1}^{infty} [a_n cos(frac{npi x}) + b_n sin(frac{npi x})] f(x) = a_0 + somme_{n = 1}^{infty} [a_n cos(frac{npi x}) + b_n sin(frac{npi x})]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/71a2f4d72f12ba29d6440b7e00367736.png)
où
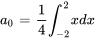
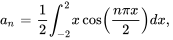
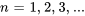
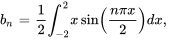
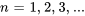
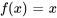 étant une fonction impaire,
étant une fonction impaire, 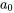 et
et 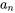 sont nuls. De même,
sont nuls. De même, 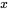 et le sinus étant tous deux des fonctions impaires, leur produit est une fonction paire. Ainsi, l’intégrale sur un intervalle symétrique de
et le sinus étant tous deux des fonctions impaires, leur produit est une fonction paire. Ainsi, l’intégrale sur un intervalle symétrique de ![[-2,2] [-2,2]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/ef8463565c3162f8ddceeb520d873307.png) peut être simplifiée en
peut être simplifiée en
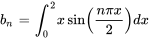
On évalue 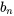 à l’aide de la technique de l’intégration par parties.
à l’aide de la technique de l’intégration par parties.
![= [-(2x) / (npi)cos((npix) / 2)]_0^2 + 2 / (npi) int_0^2cos((npix) / 2 )dx = [-(2x) / (npi)cos((npix) / 2)]_0^2 + 2 / (npi) int_0^2cos((npix) / 2 )dx](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/ee2f315dfd92ffe0c76e4075db0a1e2b.png)
![= [-(2x) / (npi)cos((npix) / 2) + 4 / (npi)^2 sin((npix) / 2 )]_0^2 = [-(2x) / (npi)cos((npix) / 2) + 4 / (npi)^2 sin((npix) / 2 )]_0^2](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/cbc0f94be4fbad554f50070e1867ff6a.png)
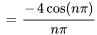
Étant donné 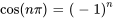 ,
, 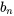 est simplifié en
est simplifié en
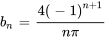
La série de Fourier est donc
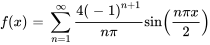
La figure ci-dessous représente graphiquement 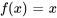 (ligne noire pleine) et son approximation par les sommes partielles de sa série de Fourier sur
(ligne noire pleine) et son approximation par les sommes partielles de sa série de Fourier sur ![[-2,2] [-2,2]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/ef8463565c3162f8ddceeb520d873307.png) pour
pour 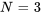 (courbe en pointillés bleus) et
(courbe en pointillés bleus) et 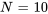 (courbe en pointillés rouges).
(courbe en pointillés rouges).
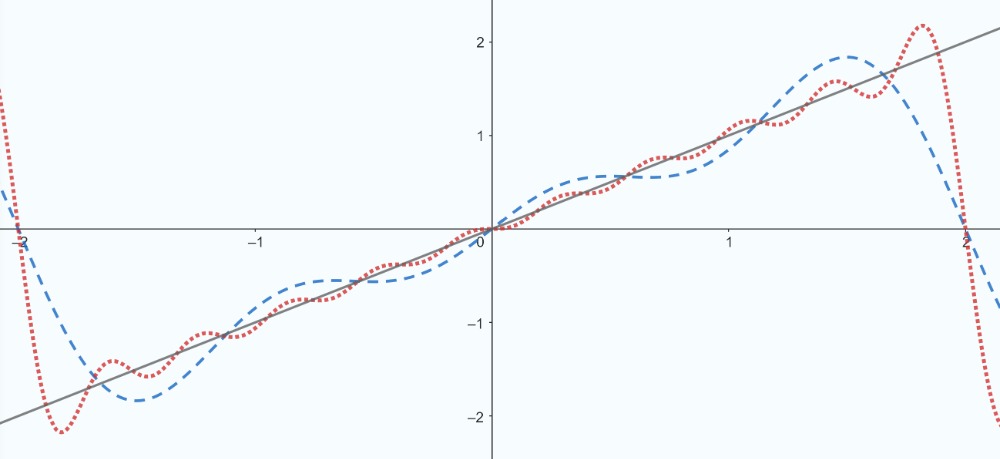
La figure interactive ci-dessous présente une comparaison visuelle entre l’approximation de la série de Fourier d’une fonction mathématique et la fonction linéaire 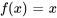 , tracée sur l’intervalle
, tracée sur l’intervalle ![[−2,2] [−2,2]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/831ced5ca2e4ac94c223e66ad444a634.png) . L’approximation de la série de Fourier, représentée par une ligne en pointillés bleus, illustre la manière dont une fonction peut être représentée comme une somme de fonctions sinusoïdales plus simples. Le nombre de termes inclus dans l’approximation de la série de Fourier peut être ajusté dynamiquement à l’aide d’un curseur interactif, allant de 1 à 10 termes. Cette caractéristique permet d’observer l’impact de l’augmentation du nombre de termes de la série sur la précision de l’approximation de la fonction réelle. La fonction linéaire
. L’approximation de la série de Fourier, représentée par une ligne en pointillés bleus, illustre la manière dont une fonction peut être représentée comme une somme de fonctions sinusoïdales plus simples. Le nombre de termes inclus dans l’approximation de la série de Fourier peut être ajusté dynamiquement à l’aide d’un curseur interactif, allant de 1 à 10 termes. Cette caractéristique permet d’observer l’impact de l’augmentation du nombre de termes de la série sur la précision de l’approximation de la fonction réelle. La fonction linéaire 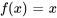 est représentée par une ligne pleine rouge pour référence.
est représentée par une ligne pleine rouge pour référence.
Trouver la série de Fourier Series de 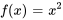 sur
sur ![[-2,2] [-2,2]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/ef8463565c3162f8ddceeb520d873307.png) .
.
Afficher/Masquer la solution
L’extrémité 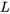 est 2. La série de Fourier est donc
est 2. La série de Fourier est donc
![f(x) = a_0 + somme_{n = 1}^{infty} [a_n cos(frac{npi x}) + b_n sin(frac{npi x})] f(x) = a_0 + somme_{n = 1}^{infty} [a_n cos(frac{npi x}) + b_n sin(frac{npi x})]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/71a2f4d72f12ba29d6440b7e00367736.png)
où
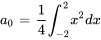
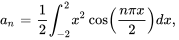
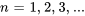
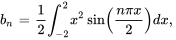
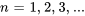
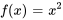 est une fonction paire, alors que le sinus est une fonction impaire, de sorte que leur produit est une fonction impaire. Ainsi,
est une fonction paire, alors que le sinus est une fonction impaire, de sorte que leur produit est une fonction impaire. Ainsi, 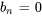 . Le produit du cosinus (aussi une fonction paire) et de
. Le produit du cosinus (aussi une fonction paire) et de 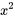 est une fonction paire, de sorte que
est une fonction paire, de sorte que 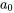 et
et 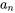 peuvent être simplifiés en
peuvent être simplifiés en
![a_0 = 1 / 2 int_{0}^ x^2 dx = 1 / 2[x^3 / 3]_0^2 = 4 / 3 a_0 = 1 / 2 int_{0}^ x^2 dx = 1 / 2[x^3 / 3]_0^2 = 4 / 3](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/98bb30911e9d0606e28c629f39ff5c90.png)
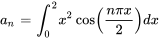
Pour évaluer 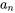 , il faut utiliser la technique d’intégration par parties deux fois.
, il faut utiliser la technique d’intégration par parties deux fois.
![= [(2x^2) / (npi)sin((npix) / 2)]_0^2-4 / (npi) int_0^2 xsin((npix) / 2 ) dx = [(2x^2) / (npi)sin((npix) / 2)]_0^2-4 / (npi) int_0^2 xsin((npix) / 2 ) dx](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/c82846c6e37aa3b1c10f4158ec167e0a.png)
![= [(2x^2) / (npi)sin((npix) / 2)-16 / (npi)^3((-npi) / 2xcos((npix) / 2) + sin((npix) / 2))]_0^2 = [(2x^2) / (npi)sin((npix) / 2)-16 / (npi)^3((-npi) / 2xcos((npix) / 2) + sin((npix) / 2))]_0^2](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/f7cbc193b0ec6fb70a3a01f669ad0db2.png)
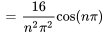
Étant donné 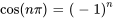 ,
, 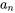 peut être simplifié en
peut être simplifié en
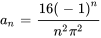
La série de Fourier est donc
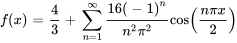
La figure ci-dessous représente graphiquement 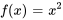 (ligne noire pleine) et son approximation par les sommes partielles de sa série de Fourier sur
(ligne noire pleine) et son approximation par les sommes partielles de sa série de Fourier sur ![[-2,2] [-2,2]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/ef8463565c3162f8ddceeb520d873307.png) pour
pour 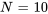 (courbe en pointillés rouges).
(courbe en pointillés rouges).
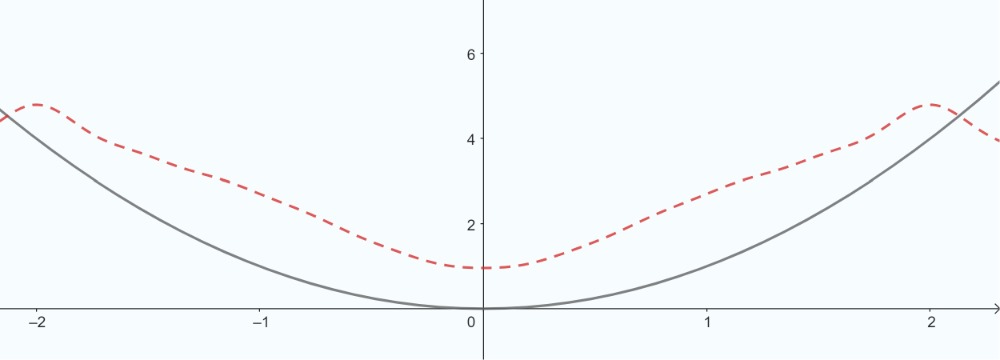
La figure interactive ci-dessous présente une comparaison visuelle entre l’approximation de la série de Fourier d’une fonction mathématique et la fonction linéaire 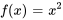 , tracée sur l’intervalle
, tracée sur l’intervalle ![[−2,2] [−2,2]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/831ced5ca2e4ac94c223e66ad444a634.png) . L’approximation de la série de Fourier, représentée par une ligne en pointillés bleus, illustre la manière dont une fonction peut être représentée comme une somme de fonctions sinusoïdales plus simples. Le nombre de termes inclus dans l’approximation de la série de Fourier peut être ajusté dynamiquement à l’aide d’un curseur interactif, allant de 1 à 10 termes. Cette caractéristique permet d’observer l’impact de l’augmentation du nombre de termes de la série sur la précision de l’approximation de la fonction réelle. La fonction
. L’approximation de la série de Fourier, représentée par une ligne en pointillés bleus, illustre la manière dont une fonction peut être représentée comme une somme de fonctions sinusoïdales plus simples. Le nombre de termes inclus dans l’approximation de la série de Fourier peut être ajusté dynamiquement à l’aide d’un curseur interactif, allant de 1 à 10 termes. Cette caractéristique permet d’observer l’impact de l’augmentation du nombre de termes de la série sur la précision de l’approximation de la fonction réelle. La fonction 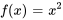 est représentée par une ligne pleine rouge pour référence.
est représentée par une ligne pleine rouge pour référence.
Prenons un exemple
Section 7.2 Exercices
- Trouve la série de Fourier pour
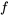 sur l’intervalle donné.
sur l’intervalle donné.
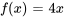 ,
, ![[-1,1] [-1,1]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/557727178bd58255d8caa19f5372ddb4.png)
Afficher/Masquer la réponse
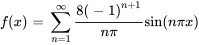
- Trouve la série de Fourier pour
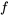 sur l’intervalle donné.
sur l’intervalle donné.
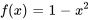 ,
, ![[-1,1] [-1,1]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/557727178bd58255d8caa19f5372ddb4.png)
Afficher/Masquer la réponse